部分分1:暴力算法(O(n^2m^2)),期望得分(20pts)。
部分分2:考虑枚举每个矩形的右上角。
转而考虑每一个点作为右上角能产生多少面积的矩形。
预处理数组(rht[i][j]),代表从点((i,j))最远可以向右走多少。
那么每次枚举一个点,枚举向下延伸多长,可以得到以这条边最远能向右平移多远。
然后一个等差数列求和计算贡献。复杂度(O(n^2m))
期望得分(50pts),实际得分(80pts)。
代码仅供参考:
#include<bits/stdc++.h>
using namespace std;
const int maxn=2e3+5;
int n,m,a[maxn][maxn];
long long ans;
int rht[maxn][maxn];
int main(){
cin>>n>>m;
string s;
for(int i=1;i<=n;i++){
cin>>s;
for(int j=1;j<=m;j++)
a[i][j]=(s[j-1]=='.');
}
for(int i=1;i<=n;i++)
for(int j=m;j>=1;j--)
if(a[i][j])rht[i][j]=rht[i][j+1]+1;
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++){
int mn=1e9;
for(int k=i;k<=n;k++){
mn=min(mn,rht[k][j]);
if(!mn)break;
ans+=1ll*(k-i+1)*(1+mn)*mn/2;
}
}
printf("%lld
",ans);
return 0;
}
正解:考虑每个矩形的底边。
转而考虑每个横向边可以向上生成多少个矩形。
预处理(up[i][j]),其含义与(rht[i][j])类似。
考虑用单调栈边维护边计算贡献。
若新加入的点比栈顶小,则其状态由 变为
变为
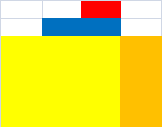
红色部分即为贡献部分。
设其宽度为(w),高度区间为([x,y])。
宽度的贡献:(W_{wide}=sumlimits_{i=1}^w i*(w-i+1)=w*sumlimits_{i=1}^w i-sumlimits_{i=1}^w i^2+sumlimits_{i=1}^w i=frac12 w*w*(w+1)-frac16 w*(w+1)*(2w+1)+frac12 w*(w+1)=frac16 w*(w+1)*(w+2))
(宽度为(i)的有(w-i+1)种选法)
长度的贡献:(W_{length}=sumlimits_{i=x}^y i=frac12 (y-x+1)*(x+y)),总贡献即为两式相乘。
最后计算还在栈中的数据时记得要从此处算到尾,如图
注意这种情况:
当当前的点比栈中第二大的还小时,则只去上面的部分,这些贡献将会被分层计算到,如图。
代码仅供参考:
#include<bits/stdc++.h>
using namespace std;
const int maxn=2e3+5;
typedef long long ll;
int n,m,a[maxn][maxn];
ll ans;
int up[maxn][maxn];
struct node{int h,x;};
stack<node>st;
inline ll sum(int x,int y,int z){
return 1ll*(x+y)*(y-x+1)*z*(z+1)*(z+2)/12;
}
int main(){
cin>>n>>m;
string s;
for(int i=1;i<=n;i++){
cin>>s;
for(int j=1;j<=m;j++)
a[i][j]=(s[j-1]=='.');
}
for(int j=1;j<=m;j++)
for(int i=1;i<=n;i++)
if(a[i][j])up[i][j]=up[i-1][j]+1;
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
int tmp=j;
while(!st.empty()){
node tp=st.top();
if(up[i][j]==tp.h)break;
else if(up[i][j]>tp.h){
st.push((node){up[i][j],tmp});break;
}else{
st.pop();tmp=tp.x;
int hh=up[i][j];
if(st.size())hh=max(hh,st.top().h);
ans+=1ll*sum(hh+1,tp.h,j-tp.x);
}
}
if(st.empty())st.push((node){up[i][j],tmp});
}
while(!st.empty()){
node tp=st.top();st.pop();
if(st.empty())ans+=1ll*sum(1,tp.h,m-tp.x+1);
else ans+=1ll*sum(st.top().h+1,tp.h,m-tp.x+1);
}
}
printf("%lld
",ans);
return 0;
}
深深地感到自己的弱小。