最小生成树Prim算法和Kruskal算法

引言

　　在了解两种最小生成树算法之前，我们要先清楚几个概念：

• 有向图：若图中的每条边都是有方向的，各点之间只能单向传递信息，则此图为有向图。
• 无向图：若图中的每条边都是没有方向，各点之间可以双向传递信息，则此图为无向图。
• 连通图：在无向图中，若任意两个顶点之间都有路径相通，则称该无向图为连通图。
• 生成树：只要能连通所有顶点而又不产生回路的任何子图都是它的生成树。
• 最小生成树：在连通网的所有生成树中，所有边的代价和最小的生成树，称为最小生成树。 

　　我们所要讲解的最小生成树，是基于无向图的基础上进行的。

1.Prim算法

　　此算法是通过逐步“加点”完成的-------------------------------------------------------------------------------

　　思路：选择任意一个顶点，每次选择到当前顶点距离最近的点，把该点与顶点之间的边加入到树中，直到各顶点都有边连接并且属于同一棵树中，

　　在找距离最近的点的时候用到了贪心。

　　方法：1.选择一个任意顶点，用标记变量进行标记

　　　　　2.计算与此顶点相连的所有点与此顶点的距离，选择最短的那个点，进行标记，加入最小生成树，以此类推

　　　　　3.直到最小生成树有n个顶点为止

　　时间复杂度：这里记顶点数v，边数e ，邻接矩阵:O(v²)   邻接表:O(elog₂v)

　　图片演示：

　　

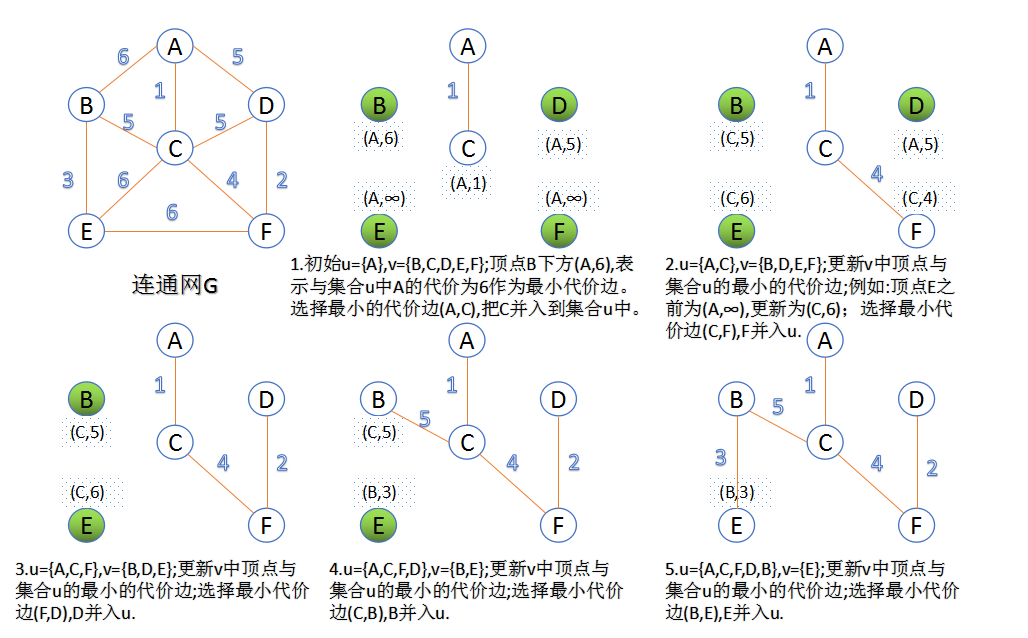
　　代码演示：（就拿数据结构实验之图论九：最小生成树这道题来说）

void prim(int n)//Prim算法
{
    flag=0;
    sum=0;
    int k=1;
    for(int i=1; i<=n; i++)
    {
        lowcost[i]=Map[i][1];//让lowcost数组等于该点到1的成本，默认各点到1的成本都为最低
    }
    vis[1]=1;//用vis数组进行标记
    for(int i=1; i<n; i++)
    {
        int t=MAX;
        for(int j=1; j<=n; j++)
        {
            if(!vis[j]&&Map[j][k]<lowcost[j])//将各点的最低成本更新进去
            {
                lowcost[j]=Map[j][k];//如果出现了更低的成本，则将该点的最低成本更新
            }
        }
        for(int j=1; j<=n; j++)
        {
            if(!vis[j]&&t>lowcost[j])//遍历没有被找过的点，找最低的成本
            {
                t=lowcost[j];
                k=j;
            }
        }
        if(t==MAX)//如果不能找到，停止
        {
            flag=1;
            return ;
        }
        vis[k]=1;
        sum+=t;
    }
}

2.Kruskal算法

　　此算法是通过逐步“加边”完成的----------------------------------------------------------------------------

　　思路：找最短的一条边，进行标记，依次找最短的边，直到最小生成树有n-1条边为止。

　　在找最短边的过程中也用到了贪心

　　方法：1.先将该树中的各边权值按从小到大顺序排列

　　　　　2.找权值最小的那条边，进行标记，再依次选择权值最小的边，注意：再次选择的边所连接的两个点，原本应属于不同的树，将这两棵树合并成同一棵树

　　　　　3.循环直到最小生成树中存在n-1条边为止

　　　　　4.还用到了并查集的思想

　　时间复杂度：elog₂e  e为图中的边数

　　图片演示：

      

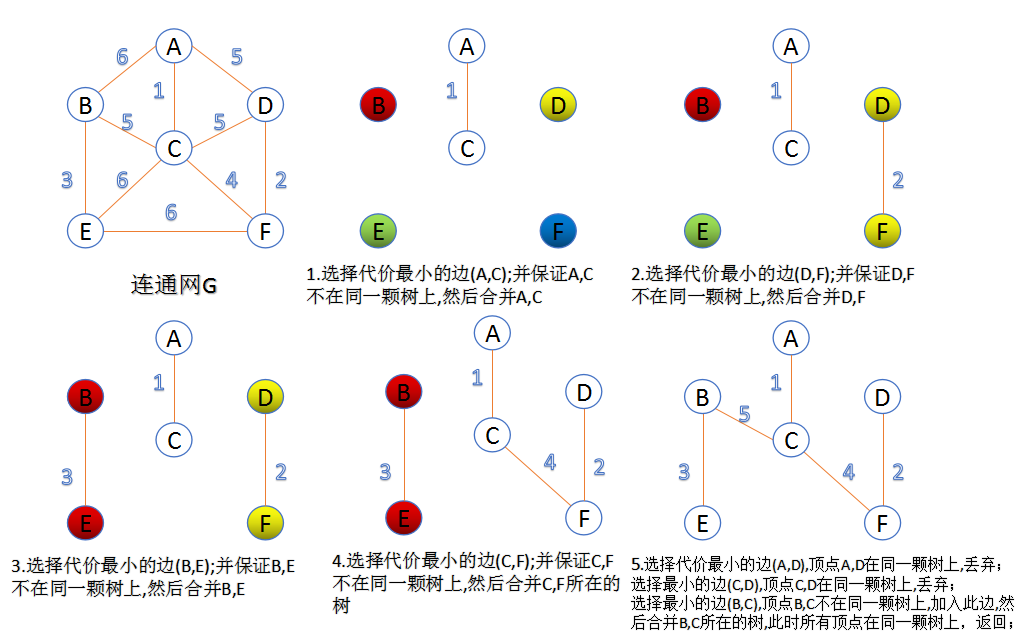
　　代码演示：（就拿数据结构实验之图论九：最小生成树这道题来说）

int find_dad(int a)//找a的上级结点
{
    if(father[a]==a)
        return a;
    return father[a]=find_dad(father[a]);
}
 
int union_node(int x,int y)//将找到的结点合并起来
{
    int x1=find_dad(x);
    int y1=find_dad(y);
 
    if(x1!=y1)
    {
        father[x1]=y1;
        return 1;
    }
    return 0;
}
 
bool cmp(edge a,edge b)//找最短的路径
{
    return a.w<b.w;
}

　　小声bb：并查集不会的以后会讲