| 项目 | 内容 |
|---|---|
| 本作业属于北航软件工程课程 | 2020春季计算机学院软件工程(罗杰 任建) |
| 本作业的要求请点击链接查看 | 2020BUAA软件工程个人项目作业 |
| 教学班级 | 005 |
| Github项目地址 | https://github.com/syncline0605/IntersectProject |
| 我在这个课程的目标 | 提高自身的代码能力、学习团队协作开发的过程 |
| 本作业帮助我实现目标的具体方面 | 实践PSP过程、熟悉用VS进行C++开发的流程、熟悉VS带有的各种工具 |
PSP表格
在开始实现程序之前,在下述PSP表格记录下你估计将在程序的各个模块的开发上耗费的时间
| PSP2.1 | Personal Software Process Stages | 预估耗时(分钟) | 实际耗时(分钟) |
|---|---|---|---|
| Planning | 计划 | ||
| - Estimate | - 估计这个任务需要多少时间 | ||
| Development | 开发 | 660 | 930 |
| - Analysis | - 需求分析(包括学习新技术) | 180 | 240 |
| - Design Spec | - 生成设计文档 | 30 | 30 |
| - Design Review | - 设计复审(和同事审核设计文档) | 30 | 0 |
| - Coding Standard | - 代码规范(为目前的开发制定合适的规范) | 60 | 0 |
| - Design | - 具体设计 | 60 | 60 |
| - Coding | - 具体编码 | 120 | 420 |
| - Code Review | - 代码复审 | 60 | 0 |
| - Test | - 测试(自我测试,修改代码,提交修改) | 120 | 180 |
| Reporting | 报告 | 180 | 210 |
| - Test Report | - 测试报告 | 120 | 120 |
| - Size Measurement | - 计算工作量 | 30 | 30 |
| - Postmortem & Process Improvement Plan | - 事后总结,并提出过程改进计划 | 30 | 60 |
| 合计 | 840 | ||
前期设计阶段的时间较为宽松,可以不断修改设计、查询新的方法,而且一边设计一边编写作业博客。在推翻一版设计之后又删掉已经写好的博客,因此耗费了许多时间。在编码阶段,因为不熟悉C++语言,处理C++的语法错误耗费了巨大的时间,有时会使用几个小时寻找一个原本很简单的小错误,但总得来说因为前期已经设计好了代码结构,在语法错误之外没有太大的阻碍。在分析、测试阶段,因为剩余时间相当不足,没有时间完整地完成PSP流程、没能做好代码风格分析、运行分析和单元测试。
总得来说,在这次的个人项目中,我深深地体会到了“先设计后编码”的优越性;但是一方面由于前期设计用时过长、中期语言不熟悉编码错误过多,导致后劲不足,虎头蛇尾,在后期分析测试阶段没有完成作业要求,没有完全消除程序警告。在作业时间截至后我将会继续认真完成这一部分。
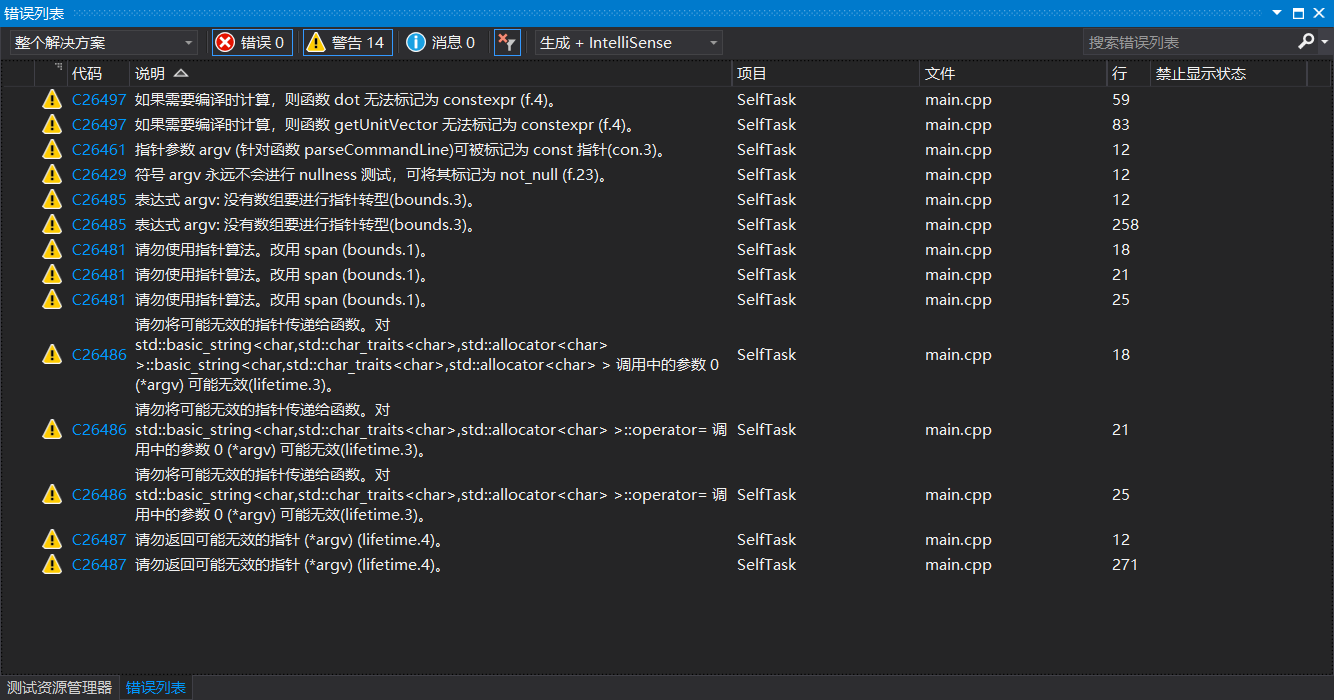
解题思路描述
需求分析(包括学习新技术)
1、在阅读了个人项目作业后,首先针对评分规则,计划学习了以下新技术:
- 因为评分标准中包含
Commit 信息是否区分标题和详细描述,参考学习了以下博客
2、程序的输入为命令行参数,需要设计并编写解析命令行参数的函数
- 因为该程序必然有一个输入 (-i) 和一个输出 (-o) ,可以基于这一点简化程序
3、针对求直线与直线交点、直线与圆交点、圆与圆的交点的问题的编程解决方法,经过学习决定应用以下方法:
-
大体思路:首先判断是否有交点,如有交点再计算交点的坐标;将判断和计算的函数不分开书写,因此许多计算的中间数据就不必重复计算
-
点在直线上的投影
- 直线从 (P_1) 指向 (P_2) 的单位向量为 e ,直线上的两点为 (P_1、P_2) ,待求的点为 (P) ,投影点为 (P_r)
- 求出向量 (<P_1, P>) 在 e 方向上的投影向量 (<P_1, P_r>),结合 (P_1) 的坐标, (P_r) 的坐标也就很容易求出了
-
直线与直线交点
-
当两直线斜率相同或两直线斜率均不存在时,两直线无交点
-
若一条直线经过两点 (P_1, P_2),则若要表示成 (Ax + By + C = 0) 的形式
-
有(A = P_1.y - P_2.y , B = P_2.x - P_1.x , C = P_1.x * P_2.y - P_2.x * P_1.y)
-
若有两条相交的直线 (A_0x + B_0y + C_0 = 0) 和 (A_1x + B_1y + C_1 = 0),它们的交点为 ((X, Y))
(X = (B_0*C_1 - B_1*C_0)/D)
(Y = (A_1*C_0 - A_0*C_1)/D)
(D = (A_0*B_1 - A_1*B_0)) (若D为0则两条直线平行)
-
-
直线与圆交点
- 先求圆心 (p) 在直线上的投影点 (pr) 的坐标,然后就可求出
Vector <p, pr>的模长 (m) ,将这个模长 (m) 与半径 (r) 比较 - 若 (m) 大于半径 (r) ,无交点
- 若 (m) 等于半径 (r) ,有一个交点,则投影点 (pr) 就是交点
- 若 (m) 小于半径 (r) ,有两个交点,则先使用勾股定理,根据 (m) 与 (r) 求出圆内线段长度的一半;再根据这个线段长度、投影点坐标和直线的方向向量,得到两个交点的坐标
- 先求圆心 (p) 在直线上的投影点 (pr) 的坐标,然后就可求出
-
圆与圆的交点
- 详见以下博客
-
参考学习博客:
设计实现过程
数据保存方式的设计
-
struct Point(struct Vector)
- 当在坐标系中进行计算时,Vector是一个非常重要的概念。从数据上来说,它与点一样用一个横坐标
double x、一个纵坐标double y就可以表示,但它也应该保存模长double length
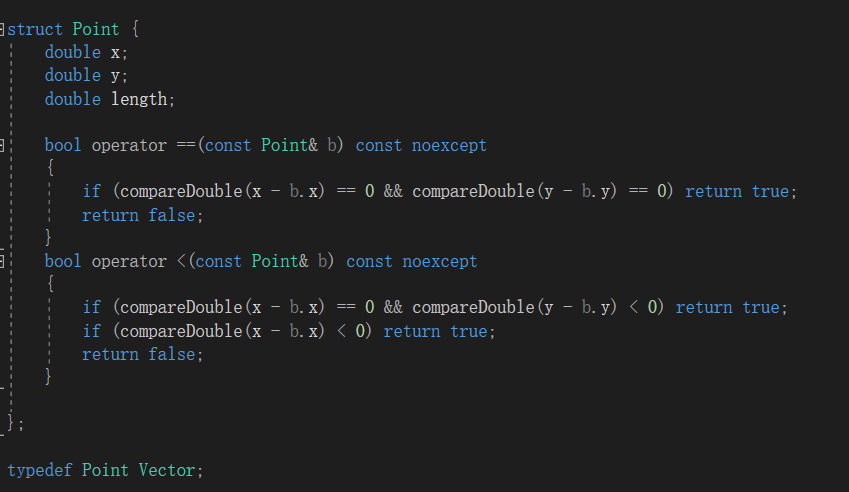
- 当在坐标系中进行计算时,Vector是一个非常重要的概念。从数据上来说,它与点一样用一个横坐标
-
struct Line
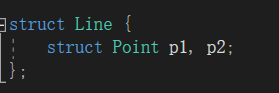
- struct Circle
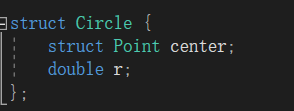
- 用
STL vector数据结构保存各输入项- vector< Line >
- vector< Circle >
- 用
STL set数据结构保存各交点,保证存储的交点不重复- set< Point >
函数的设计
-
命令行解析函数
-
输入处理函数
-
求连接两点的向量
- 输入:
Point A,Point B - 输出:
Vector M
- 输入:
-
求点在直线上的投影坐标函数
- 输入:
Point A,Line l - 输出:
point M
- 输入:
-
求点到直线的距离函数
- 输入:
Point A,Line l - 输出:
int distance
- 输入:
-
求两直线交点数的函数/求直线与圆交点数的函数/求两圆交点数的函数
- 输出:交点数
- 交点的坐标通过将引用作为参数传入函数来得到
单元测试的设计
- 没有完整地对所有函数进行单元测试,主要以使用测试用例测试为主,简单地对一些小函数进行了单元测试
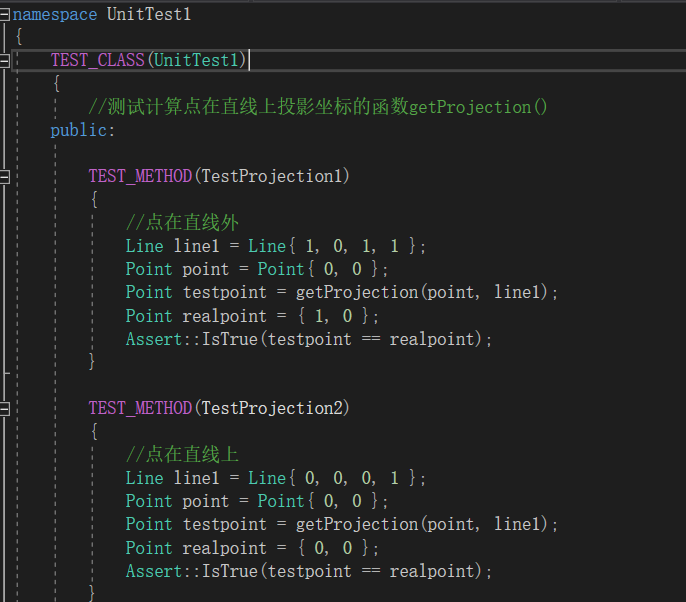
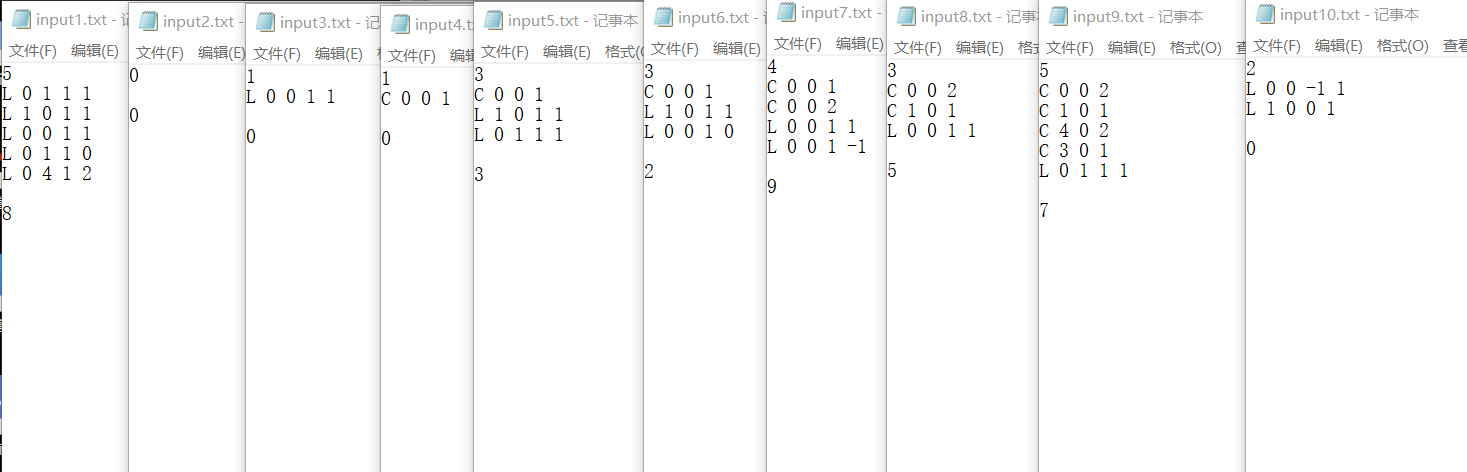
测试样例的设计
程序性能
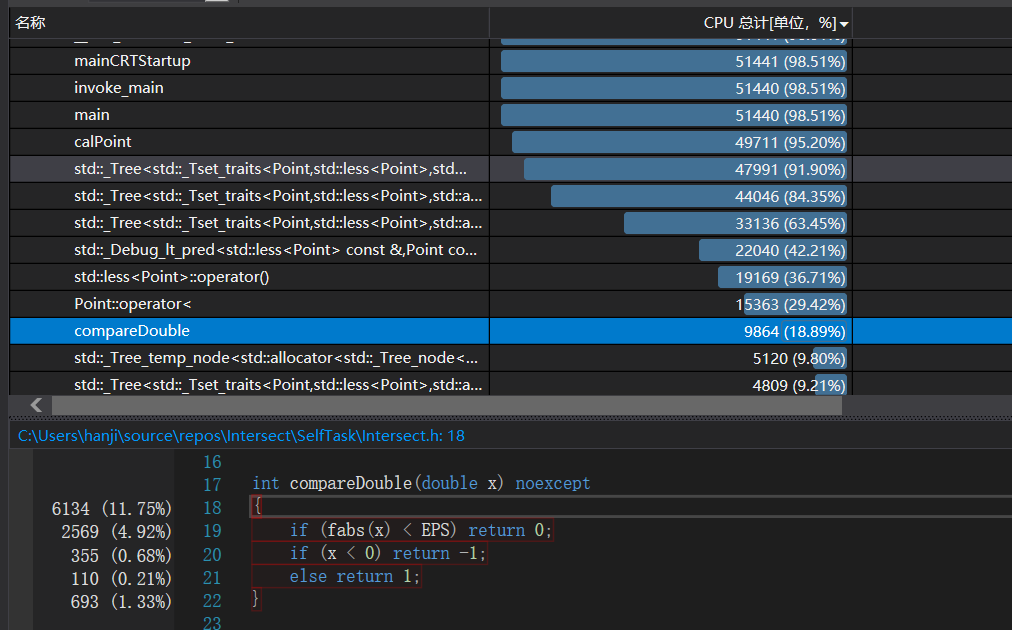
使用一个随机生成的包含一千多条数据的测试集,运行了一分钟(未运行完即终止运行)。
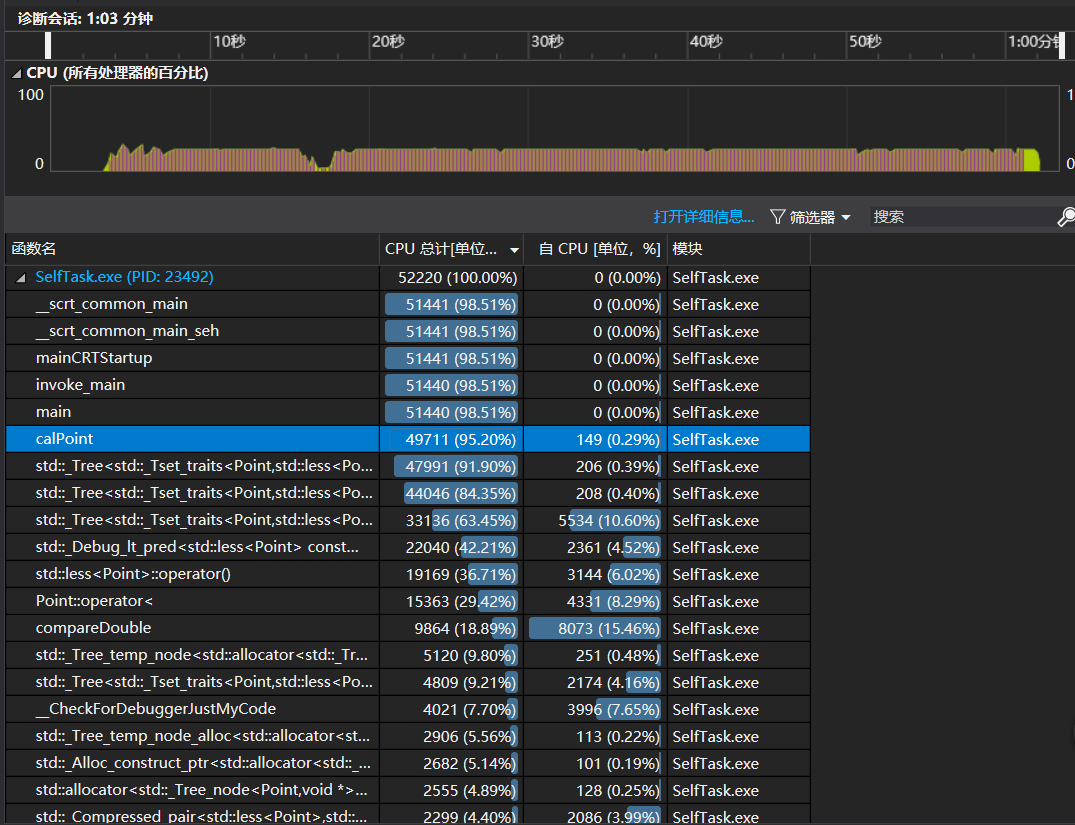
很明显,程序将大多数时间用在了set的元素插入上
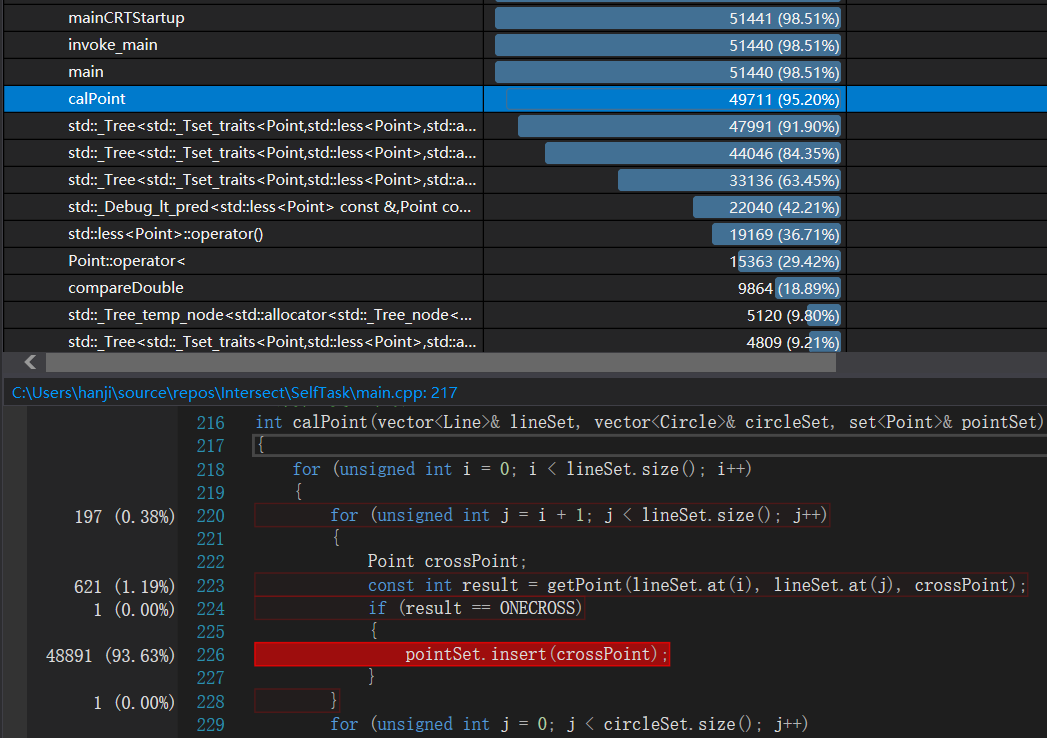
除此之外,基于确定的精确值对equals意义的重写也占用了大量时间
在设计阶段思考过这样一个优化方式,但是最后没有时间实现
- 每当计算出两直线 (l_1,l_2) 的交点或是直线 (l) 与圆 (c) 的交点后,就可以判断交点
- 是否在其余还未判断与 (l_1) 的交点、与 (l_2) 的交点的直线上,若在,则可记录下来,就不必再进行计算和判断(因为两直线只可能有一个交点)
- 是否在其余还未判断与 (l) 的交点的直线上,同上
代码说明
- 求两直线的交点
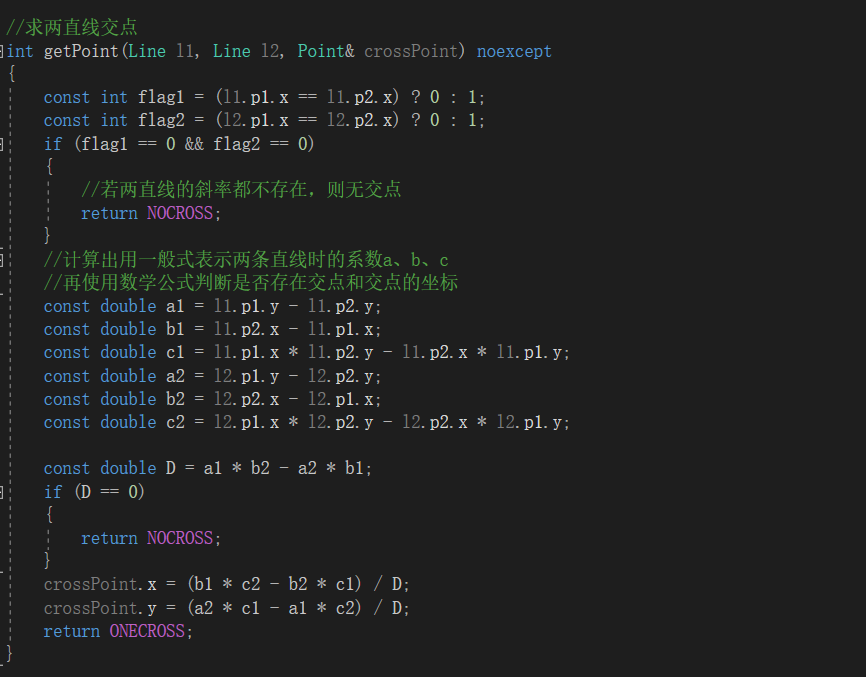
- 求直线与圆的交点
