POJ 2528 Mayor's posters

Description

The citizens of Bytetown, AB, could not stand that the candidates in the mayoral election campaign have been placing their electoral posters at all places at their whim. The city council has finally decided to build an electoral wall for placing the posters and introduce the following rules: 

• Every candidate can place exactly one poster on the wall. 
• All posters are of the same height equal to the height of the wall; the width of a poster can be any integer number of bytes (byte is the unit of length in Bytetown). 
• The wall is divided into segments and the width of each segment is one byte. 
• Each poster must completely cover a contiguous number of wall segments.

They have built a wall 10000000 bytes long (such that there is enough place for all candidates). When the electoral campaign was restarted, the candidates were placing their posters on the wall and their posters differed widely in width. Moreover, the candidates started placing their posters on wall segments already occupied by other posters. Everyone in Bytetown was curious whose posters will be visible (entirely or in part) on the last day before elections. 
Your task is to find the number of visible posters when all the posters are placed given the information about posters' size, their place and order of placement on the electoral wall. 

Input

The first line of input contains a number c giving the number of cases that follow. The first line of data for a single case contains number 1 <= n <= 10000. The subsequent n lines describe the posters in the order in which they were placed. The i-th line among the n lines contains two integer numbers l_i and ri which are the number of the wall segment occupied by the left end and the right end of the i-th poster, respectively. We know that for each 1 <= i <= n, 1 <= l_i <= ri <= 10000000. After the i-th poster is placed, it entirely covers all wall segments numbered l_i, l_i+1 ,... , ri.

Output

For each input data set print the number of visible posters after all the posters are placed. 

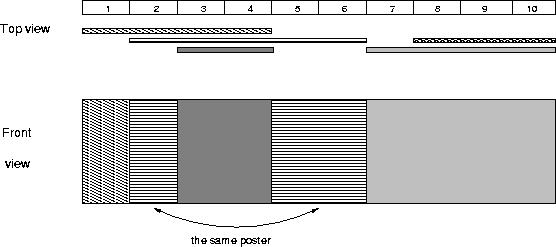
The picture below illustrates the case of the sample input. 

Sample Input

1
5
1 4
2 6
8 10
3 4
7 10

Sample Output

   4

题意：有一面墙，被等分为1QW份，一份的宽度为一个单位宽度。现在往墙上贴N张海报，每张海报的宽度是任意的，但是必定是单位宽度的整数倍，且<=1QW。后贴的海报若与先贴的海报有交集，后贴的海报必定会全部或局部覆盖先贴的海报。现在给出每张海报所贴的位置（左端位置和右端位置），问张贴完N张海报后，还能看见多少张海报？（PS：看见一部分也算看到。）

考查了线段树（覆盖问题）及离散化处理：

离散化处理：

  通俗点说，离散化就是压缩区间，使原有的长区间映射到新的短区间，但是区间压缩前后的覆盖关系不变。举个例子：

  有一条1到10的数轴（长度为9），给定4个区间[2,4] [3,6] [8,10] [6,9]，覆盖关系就是后者覆盖前者，每个区间染色依次为 1 2 3 4。

  现在我们抽取这4个区间的8个端点，2 4 3 6 8 10 6 9

  然后删除相同的端点，这里相同的端点为6，则剩下2 4 3 6 8 10 9

  对其升序排序，得2 3 4 6 8 9 10

  然后建立映射

  2     3     4     6     8     9     10

  ↓     ↓     ↓      ↓      ↓     ↓      ↓

  1     2     3     4     5     6     7

  那么新的4个区间为 [1,3] [2,4] [5,7] [4,6]，覆盖关系没有被改变。新数轴为1到7，即原数轴的长度从9压缩到6，显然构造[1,7]的线     段树比构造[1,10]的线段树更省空间，搜索也更快，但是求解的结果却是一致的。

 

  附：海报张数上限为10000，即其端点映射的新数轴长度最多为20000。因此建立长度为1QW的离散数组dis时，其映射值最多为    20000，这样可以节约空间开销。

#include<stdio.h>
#include<algorithm>
#define N 10010
using namespace std;
struct node
{
    int left, right, covered; //covered表示该区间是否被覆盖
}no[8*N];
struct point
{
    int L, R;
}po[N];
int Hash[10000010], A[2*N]; //A数组保存未离散化处理之前的端点的值，Hash数组存放离散化处理后的端点
void Bulid(int left, int right, int root)
{
    int mid;
    no[root].left = left;
    no[root].right = right;
    no[root].covered = 0;
    if (left == right) return ;
    mid = (left+right)/2;
    Bulid(left, mid, root*2);
    Bulid(mid+1, right, root*2+1);
}
int Query(int left, int right, int root)
{
    int mid, a1, a2;
    if (no[root].covered) return 0;
    if (no[root].left == left && no[root].right == right)
    {
        no[root].covered = 1;
        return 1;
    } //找到该区间并且未被覆盖，则该区间可以贴上海报，covered赋值为1，下次不能再贴上海报
    mid = (no[root].left+no[root].right)/2;
    int ans; //不能直接返回值
    if (right <= mid) ans = Query(left, right, root*2);
    else if (left > mid) ans = Query(left, right, root*2+1);
    else
    {
        a1 = Query(left, mid, root*2);
        a2 = Query(mid+1, right, root*2+1);
        ans = a1 | a2;
    }
    if (no[root*2].covered && no[root*2+1].covered)
        no[root].covered = 1;
    return ans; //整个区间都需要更新是否被覆盖
}
int main ()
{
    int T, n, i, k, ans;
    scanf("%d", &T);
    while (T--)
    {
        k = 1;
        ans = 0;
        scanf("%d", &n);
        for (i = 1; i <= n; i++)
        {
            scanf("%d%d", &po[i].L, &po[i].R);
            A[k++] = po[i].L;
            A[k++] = po[i].R;
        }
        k--;
        sort(A+1, A+k+1); //排序（从小到大）
        k = unique(A+1, A+k+1)-(A+1); //去重
        for (i = 1; i <= k; i++)
            Hash[A[i]] = i; //离散化处理
        Bulid(1, k, 1);
        for (i = n; i >= 1; i--)
        {
            if (Query(Hash[po[i].L], Hash[po[i].R], 1))
                ans++;
        } //从后往前判断每一个区间是否还能贴上报纸，因为如果从前往后无论怎样都可以贴，无法判断是否此区间被覆盖
        printf("%d
", ans);
    }
    return 0;
}