已知二叉树先序和中序，求后序。

从http://www.cnblogs.com/fzhe/archive/2013/01/07/2849040.html处转载。

一、已知前序、中序遍历，求后序遍历

例：

前序遍历:         GDAFEMHZ

中序遍历:         ADEFGHMZ

画树求法：第一步，根据前序遍历的特点，我们知道根结点为G

              第二步，观察中序遍历ADEFGHMZ。其中root节点G左侧的ADEF必然是root的左子树，G右侧的HMZ必然是root的右子树。

              第三步，观察左子树ADEF，左子树的中的根节点必然是大树的root的leftchild。在前序遍历中，大树的root的leftchild位于root之后，所以左子树的根节点为D。

              第四步，同样的道理，root的右子树节点HMZ中的根节点也可以通过前序遍历求得。在前序遍历中，一定是先把root和root的所有左子树节点遍历完之后才会遍历右子树，并且遍历的左子树的第一个节点就是左子树的根节点。同理，遍历的右子树的第一个节点就是右子树的根节点。

            第五步，观察发现，上面的过程是递归的。先找到当前树的根节点，然后划分为左子树，右子树，然后进入左子树重复上面的过程，然后进入右子树重复上面的过程。最后就可以还原一棵树了。该步递归的过程可以简洁表达如下：

1 确定根,确定左子树，确定右子树。

2 在左子树中递归。

3 在右子树中递归。

4 打印当前根。

那么，我们可以画出这个二叉树的形状：

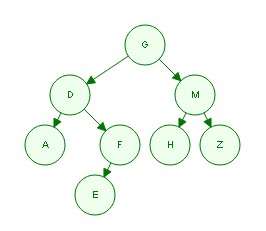
那么，根据后序的遍历规则，我们可以知道，后序遍历顺序为：AEFDHZMG

编程求法：（依据上面的思路，写递归程序）

#include <stdio.h>
#include <string.h>

void TreeSequence(char * pre , char  * order , int length )
{
    if(0 == length)
    {
        return ;
    }

    char data = * pre ;
    int rootpos=0 ;
    for( ;rootpos<length ; rootpos++)
    {
        if( * pre == order[rootpos])
            break ;
    }

    TreeSequence(pre+1 ,order, rootpos) ;  //
    TreeSequence(pre + rootpos + 1, order + rootpos +1, length-(rootpos+1)) ; //
    printf("%c" ,data) ;

}

int main()
{
    char str1[105],str2[105] ;
    printf("请输入先序遍历的字符：") ;
    scanf("%s" , str1) ;
    printf("请输入中序遍历的字符：") ;
    scanf("%s" , str2) ;
    printf("输出后序遍历的字符：") ;
    int length = strlen(str1) ;
    TreeSequence( str1 , str2 , length) ;
    printf("
") ;
}