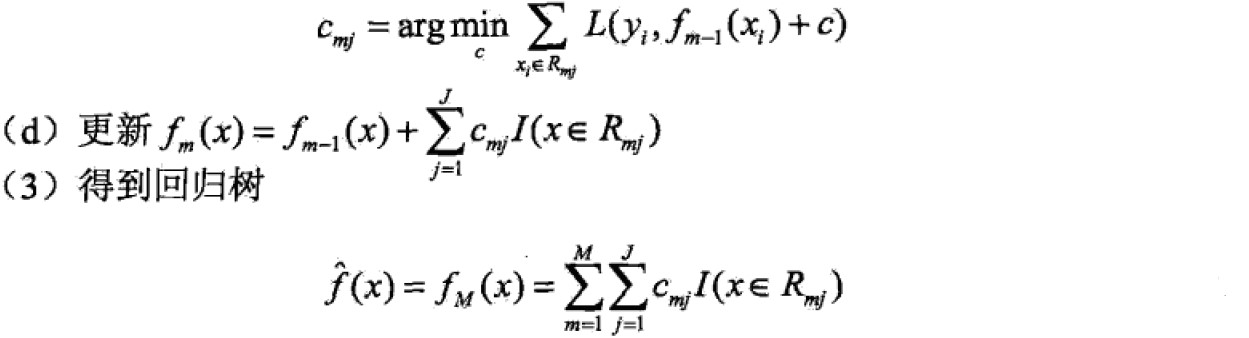2 AdaBoost训练误差分析
3 AdaBoost algorithm 另外的解释
3.1 前向分步算法
3.2 前向分步算法与AdaBoost
4 提升树
4.1 提升树模型
4.2 梯度提升
Boosting在分类问题中，通过改变训练样本的权重，学习多个分类器，并将这些分类器进行线性组合，提高分类性能。AdaBoost最具代表性，由Freund和Schapire在1995年提出；Boost树在2000年由Friedman提出。
1 AdaBoost算法
基本思想：对于分类而言，给定一个训练样本集，求比较粗糙的分类规则（弱分类器）比强分类器容易得多。因此此方法就是从弱分类器出发，反复学习，得到一系列弱分类器(基本分类器)，然后组合成一个强分类器。Boosting方法大多是改变训练数据的权值分布，针对不同训练数据分布调用弱分类器进行一系列学习的方法。如何改变训练数据的权值或概率分布？提高前一轮弱分类器错误分类的样本的权值，而降低正确分类样本的权值，这样错误分类的样本在本次弱分类器中就被更大的关注，一次分类问题就被一系列分类器分而治之。如何组合这一组弱分类器？——加权多数表决的方法，加大无误差率低的弱分类器的权值，减小误差率大的弱分类器的权值，让其在表决中起较小作用。
算法：
说明：
步骤一中，权值分布采取均匀分布得到权值向量D1，在原始数据上学习分类器；
步骤二中，m表示轮数，m=1表示第一轮学习过程。
(a)使用当前权值向量Dm加权训练集，学习基本分类器Gm(x)。
(b)计算基本分类器在加权训练集上的误分类率em，可以看出Gm(x)的分类误差率是误分类样本权重之和。
(c) Gm的系数就是在最终组合分类器所占的权重，表示此分类器的重要性。em小于1/2时，alpham>=0，随着误分类率的减小而增大，所以误分类率越小的基本分类器在最终分类器所起的作用越大。
(d)中更新权值分布，为下一轮做准备，其实yGm相乘是验证此个样本值分类的正确性，正确则同号，同号则为正，为正则指数部分为负数,就减少此样本值的分量，减少的多少由alpha决定。即
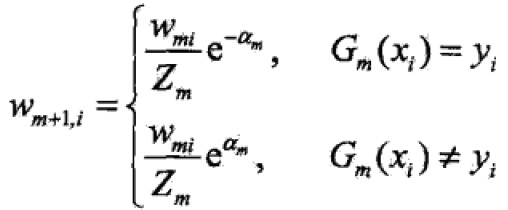
步骤三中，f(x)的线性组合实现了M个基本分类器的加权表决，系数alpha是基本分类器的重要性。注意这里的alpha之和不为1。f(x)的符号表示实例的类别，绝对值的大小表示分类的确信度。最终sign得到强分类器G(x)。
在具体执行过程中，可以每次都进行组合然后得到误分类点，直到误分类点为0为止或者达到m的最大值M为止。
2 AdaBoost训练误差分析
定理：训练误差的界：
证明：
定理：二类分类的AdaBoost训练误差界：
，
证明：
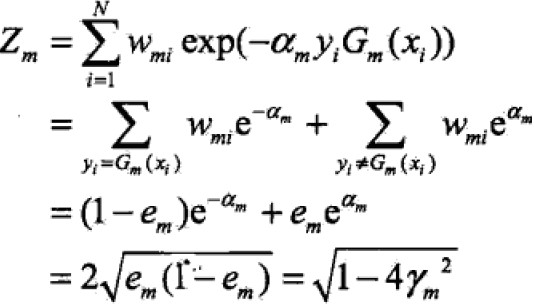
推论：
表明AdaBoost误差界以指数速率下降。
注意：AdaBoost算法不需要知道下界γ，具有适应性adaptive Boosting
3 AdaBoost algorithm 另外的解释
这个解释是AdaBoost算法模型是加法模型，损失函数是指数函数，学习算法为前向分步算法时的二类分类学习方法。
3.1 前向分步算法
加法模型（additive model）
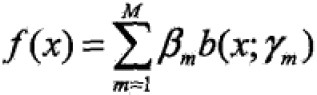
其中，b为基函数，γ为基函数的参数；β为基函数的系数；
给定训练集和损失函数L(y,f(x))条件下，学习加法模型f成为风险极小化或损失函数极小化的问题：
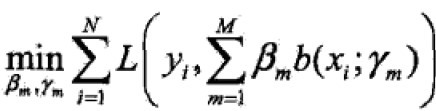
前向分步算法(forward stagewise algorithm)求解思路是：因为学习的模型是加法模型，如果能够从前向后，每一步只学习一个基函数及其系数，逐步逼近优化函数目标（上式），那么就可以简化优化的复杂度。因此，每步只需优化如下损失函数：
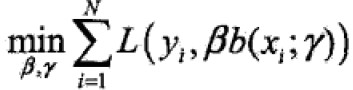
算法明细：
3.2 前向分步算法与AdaBoost
定理：AdaBoost算法是前向分步算法的特例，model为基本分类器组成的加法模型，损失函数是指数函数。
证明：根据算法流程对比二者并无区别，需要注意的是前向分步算法的损失函数是指数损失函数（exponential loss function）
4 提升树
Boosting Tree被认为是统计学习中性能最好的方法之一，以分类树或回归树为基本分类器的提升方法。
4.1 提升树模型
提升方法实际上采用的是加法模型（基函数的线性组合）与前向分步算法。以决策树为基函数的提升方法称为提升树。对分类问题的决策树是二叉分类树，对回归问题的决策树是二叉回归树。基本分类器xv可以看做由一个根结点直接连接两个叶子结点的简单决策树，即决策树桩(decision stump)。提升树模型可以表示为决策树的加法模型：
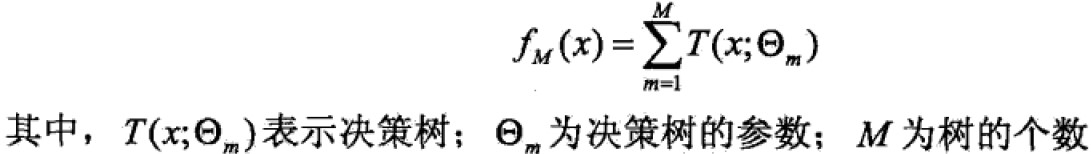
提升算法采用前向分步算法，首先确定初始提升树
，则第m步的模型是
；
经验最小化函数：
，m-1表示当前树，经验最小化函数可以确定下一个树的决策参数。
不同问题的提升树学习算法，主要区别是使用的损失函数不同（回归问题：平方误差损失函数；分类问题指数损失函数）。
回归问题
已知训练集T={(x1,x2),…(xN,yN)},x属于Rn，y属于R，如果将输入空间划分为J个互不相交的区域R1，…，RJ，并且在每个区域上确定输出常量cj,树可表示为
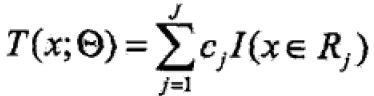
其中，
表示树的区域划分和各区域上常数（类）。J是回归树的复杂度即叶子结点个数。
回归提升树使用前向分步算法：
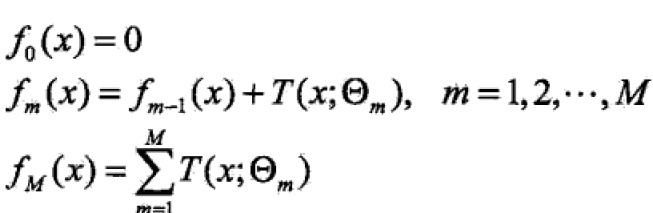
前向分步算法第m步，给定当前模型fm-1，需求：
。
当采用平方误差损失函数时， 
代入得：
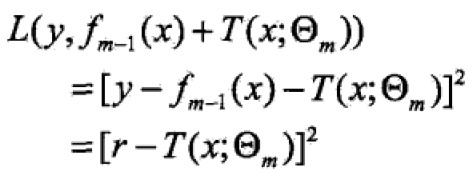
这里，
是当前模型拟合数据的残差（residual）
回归树算法：
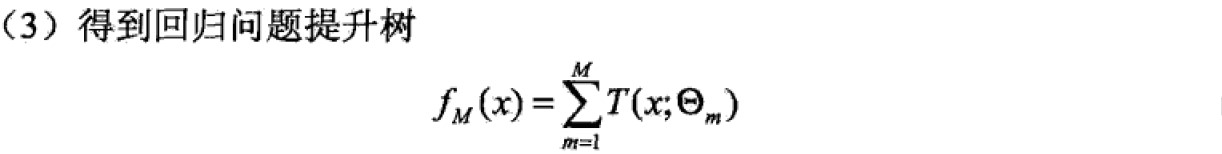
4.2 梯度提升
当损失函数不是平方误差函数或者指数函数时，优化并不简单，故提出梯度提升（gradient Boosting）算法，关键是利用损失函数的负梯度在当前模型的值
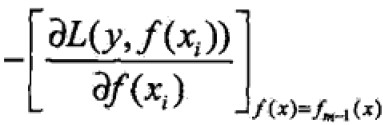作为回归问题中残差的近似值拟合回归树。
梯度提升算法：
