决策树算法

if-then规则的集合，优点是模型具有可读性，分类速度快。

 

决策树常用的算法：ID3算法、C4.5算法、CART算法

1、熵（entropy，又称信息熵） 

 

 因此，熵只依赖于X的分布，与X的取值无关。

• 熵越大，随机变量X的不确定性就越大。
• 如果有0概率，令。单位为比特(bit)或纳特(Nat)

    相关代码实现：

//根据具体属性和值来计算熵   
double ComputeEntropy(vector <vector <string> > remain_state, string attribute, string value,bool ifparent){  
    vector<int> count (2,0);  
    unsigned int i,j;  
    bool done_flag = false;//哨兵值   
    for(j = 1; j < MAXLEN; j++){  
        if(done_flag) break;  
        if(!attribute_row[j].compare(attribute)){  
            for(i = 1; i < remain_state.size(); i++){  
                if((!ifparent&&!remain_state[i][j].compare(value)) || ifparent){//ifparent记录是否算父节点   
                    if(!remain_state[i][MAXLEN - 1].compare(yes)){  
                        count[0]++;  
                    }  
                    else count[1]++;  
                }  
            }  
            done_flag = true;  
        }  
    }  
    if(count[0] == 0 || count[1] == 0 ) return 0;//全部是正实例或者负实例   
    //具体计算熵 根据[+count[0],-count[1]],log2为底通过换底公式换成自然数底数   
    double sum = count[0] + count[1];  
    double entropy = -count[0]/sum*log(count[0]/sum)/log(2.0) - count[1]/sum*log(count[1]/sum)/log(2.0);  
    return entropy;  
} 

2、条件熵——表示在已知特征A的条件下，数据集D的不确定性

 

 

 

 

　　

     条件概率公式： 

3、信息增益（偏向于选择取值较多的特征）——ID3算法

参考：http://www.cnblogs.com/mfrbuaa/p/4730248.html  Weka算法Classifier-tree-J48源代码分析（一个）基本数据结构和算法

4、信息增益比 ——C4.5算法

 

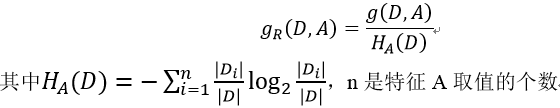
CART算法　　Classification and regression tree，分类回归树

 1、（最小二乘）回归树 —— 平方误差最小准则  

  步骤如下：

       

 2、分类树 —— 基尼指数(Gini Index)最小准则

基尼指数（表示集合D的不确定性）

 

步骤如下：

1)        针对于数据集D的每一个特征，对其所有可能的取值a，计算在时的基尼指数

2)        选择基尼指数最小的特征及其对应的切分点，作为最优特征和最优切分点。

3)        将训练集依该特征及其切分点，分配到两个子结点中，对这两个子结点递归调用（1）（2），直至满足停止条件

4)        生成CART决策树

算法停止条件：

• 　　结点中的样本个数小于预定阙值
• 　　样本集的基尼指数小于预定阙值
• 　　没有更多的特征。