1475. 商品折扣后的最终价格
难度简单
给你一个数组 prices ,其中 prices[i] 是商店里第 i 件商品的价格。
商店里正在进行促销活动,如果你要买第 i 件商品,那么你可以得到与 prices[j] 相等的折扣,其中 j 是满足 j > i 且 prices[j] <= prices[i] 的 最小下标 ,如果没有满足条件的 j ,你将没有任何折扣。
请你返回一个数组,数组中第 i 个元素是折扣后你购买商品 i 最终需要支付的价格。
示例 1:
输入:prices = [8,4,6,2,3] 输出:[4,2,4,2,3] 解释: 商品 0 的价格为 price[0]=8 ,你将得到 prices[1]=4 的折扣,所以最终价格为 8 - 4 = 4 。 商品 1 的价格为 price[1]=4 ,你将得到 prices[3]=2 的折扣,所以最终价格为 4 - 2 = 2 。 商品 2 的价格为 price[2]=6 ,你将得到 prices[3]=2 的折扣,所以最终价格为 6 - 2 = 4 。 商品 3 和 4 都没有折扣。
示例 2:
输入:prices = [1,2,3,4,5] 输出:[1,2,3,4,5] 解释:在这个例子中,所有商品都没有折扣。
示例 3:
输入:prices = [10,1,1,6] 输出:[9,0,1,6]
提示:
1 <= prices.length <= 5001 <= prices[i] <= 10^3
单调栈最全面详解,包你懂!
诺*^_^*言发布于 2020-06-22867C++栈Java
解题思路
这里我们考虑一个过程中的情况(这里维护一个单调递增的队列,!!要将所有元素都加入一次队列(一定记住这句话)):
>a0 a1 a2 a3 ... am ... an 单调递增;n可以为0个(空数列,初始情况)
现在我们判断an+1,如果an+1 <= a0 那么a0-an的元素都需要-an+1(题干说的第一个小于等于的元素要减去嘛;因为我们保证了a0-an是单调递增的了(且n=1的时候就是只有a0),所以an+1一定是第一个小于等于a0-an的),然后a0-an都出队,因为要保持这个队列单调递增的性质
此时队列为 >an+1继续假设an+1,如果an+1 > a0 && an+1 <=a1,那么a1-an的元素都需要-an+1;
原因同第一步,此时队列为 >a0 an+1继续假设an+1,如果an+1 > a1 && an+1 <=a2,那么a2-an的元素都需要-an+1;
原因同第一步,此时队列为 >a0 a1 an+1
...- 最后一种情况就是,如果an+1 > an,那么就要将an+1加入这个单调递增的队列。
此时队列为 > a0 a1 a2 ... an an+1
然后我们只需要循环上面1--4就可以了,举个栗子给大家看看!
假设本题的序列为 8 4 9 11 5 2 6 7 9 1
初始单调递增的序列为空a{}
1. -- 8<a0(没有元素的时候一定入队) -- {8}
2. -- 4<a0=8(所以a0-an出队,并且都要减去4) -- {4}
3. -- 9>an=4(所以9入队) -- {4 9}
4. -- 11>an=9(所以11入队)) -- {4 9 11}
5. -- 5>a0=4 && 5<a1=9(所以9 11 出队都减去5,然后5入队) -- {4 5}
6. -- 2>an=5(所以4 5出队都减去2,然后2入队) -- {2}
7. -- 6>a0=2(所以6入队) -- {2 6}
8. -- 7>an=6(所以7入队) -- {2 6 7}
9. -- 9>an=7(所以9入队)-- {2 6 7 9}
10. -- 1<a0=2(所以全部出队都减去1,1入队)-- {1}
******!!总结规律可以发现,我们每次比较an+1都应该从an比到a0,然后比an+1大的都出队且减an+1,最后为
an+1找到一个合适的位置,继续判断an+2,这个过程由于我们需要保存a0-an,而且比较的顺序是从后往前
这不正好满足了栈的模式么,1记忆存储,2从后往前,剩下的结合笔者代码,很容易弄懂了就。
ps:笔者也是学生,发现仔细写个解析真的好浪费时间,真的感谢网上分享解题过程的算法朋友们,真的辛苦了。
代码
c++版本
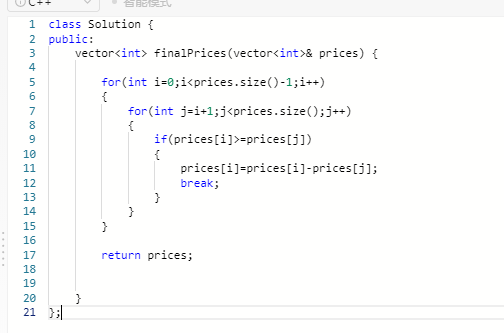
class Solution {
public:
vector<int> finalPrices(vector<int>& prices) {
stack<int> s;
int len = prices.size();
for(int i=0;i<len;i++){
if(!s.empty() && prices[i] <= prices[s.top()]){ //为空就直接push
while(!s.empty() && prices[i] <= prices[s.top()]){
int temp = s.top();
prices[temp] -= prices[i];
s.pop();
}
}
s.push(i); //保存索引,方便再次在prices中找到这个元素
}
return prices;
}
};