目录
内容简介
本次作业在建立二叉树方面,使用了先序输入建立的方法(递归实现),同时额外实现了层次输入建立的方法(队列实现)。在遍历输出方面,有先序/中序/后序/层次遍历四种。
其中,本次建立二叉树时,输入结束的条件为输入数据为-1。
生成的二叉树都长这样: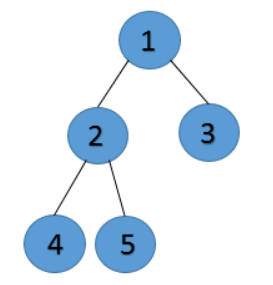
(这里是一颗完全二叉树,我的层次输入建立二叉树的函数是专门为了建立完全二叉树写的,先序输入建立的函数可以满足任何情况)
二叉树建立
1.先序输入建立二叉树
void PreCreateTree(Tree& T)//传入要生成的二叉树
{
int data;
cin >> data;
T = new TREE;
if (data == -1)//输入值为-1是递归结束条件
{
T = NULL;//这里要将结点本身指向NULL
return;
}
T->left = NULL;//new后,T的左右孩子都置为NULL
T->right = NULL;
T->data = data;
PreCreateTree(T->left);//先建立左子树
PreCreateTree(T->right);//再建立右子树
}
2.层次输入建立二叉树
void LevelCreatTree(Tree &T)
{
int i = 1,data;//data为输入的数据,i用来判定是左孩子还是右孩子(奇数为左,偶数为右)
queue<TNode> q;//用队列来存储父结点
T = new TREE;//根节点先处理
T->left = NULL;
T->right = NULL;
cin >> data;
if (data == -1)
{
T = NULL;//如果为-1记得让结点为NULL
return ;
}
T->data = data;
q.push(T);//每次生成一个新的结点,都要将这个结点入队
TNode p,parent;//p是要生成的新结点,parent是这个p结点的父结点(不要纠结为什么不用father辽)
while (1)
{
parent = q.front();//队列的首元素会是要添加结点p的父结点
q.pop();//拿了以后记得出队
for (int j = 0; j < 2; j++)//层次遍历一个父结点一次要链接左右两个孩子
{
cin >> data;
if (LevelAdd(p, parent, i, data))//这个函数返回值是bool型
{
q.push(p);//返回true代表生成成功,将新生成的结点入队
}
else
{
return;//返回false说明输入了-1,生成新结点失败,层次输入结束。
}
}
}
}
bool LevelAdd(TNode &p,TNode &parent,int &i,int data)
//传入的p代表要生成的结点,parent是这个结点的父结点,i用来判断是左孩子还是右孩子,data是要传入的数据
{
p = new TREE;
p->left = NULL;
p->right = NULL;
if (data == -1)//如果是-1,返回false且p本身指向NULL
{
p = NULL;
return false;
}
p->data = data;
if (i%2)//i是奇数的时候,p是parent的左孩子
{
parent->left = p;
}
else//i是偶数就是右孩子了
{
parent->right = p;
}
i++;//这里的i也可以代表树的结点数量
return true;
}
二叉树的遍历
1.先序遍历
①递归实现
void PreOrder(Tree& T)
{
if (T)
{
cout << T->data << ' ';
PreOrder(T->left);
PreOrder(T->right);
}
}
②栈实现
void PreOrderByStack(Tree& T)
{
stack<TNode> s;
TNode p;
p = T;
while (p || !s.empty())
{
if (p)
{
cout << p->data << ' ';//先序遍历一碰到结点就先输出值
s.push(p);//然后将这个结点入栈
}
else//没有左孩子的时候就开始往右边走
{
p = s.top();
s.pop();
p = p->right;
}
}
}
2.中序遍历
①递归实现
void InOrder(Tree& T)
{
if (T)
{
InOrder(T->left);
cout << T->data << " ";
InOrder(T->right);
}
}
②栈实现
void InOrderByStack(Tree& T)
{
TNode p;
p = T;
stack<TNode> s;
while (p || !s.empty())
{
if (p)
{
s.push(p);
p = p->left;
}
else//中序遍历是左根右这种顺序,所以先找到最左结点
{
p = s.top();
s.pop();
cout << p->data << ' ';
p = p->right;
}
}
}
3.后序遍历
递归实现
void PostOrder(Tree& T)
{
if (T)
{
PostOrder(T->left);
PostOrder(T->right);
cout << T->data << ' ';
}
}
4.层次遍历
队列实现
void LevelOrder(Tree& T)
{
queue<TNode> q;
TNode p;
p = T;
while (p)
{
cout << p->data << " ";//先将这个结点输出
q.push(p->left);
q.push(p->right);//然后左右孩子依次入队
p = q.front();
q.pop();
}
}
运行结果
输入的值为-1代表这个是空结点
生成的是这样一个二叉树: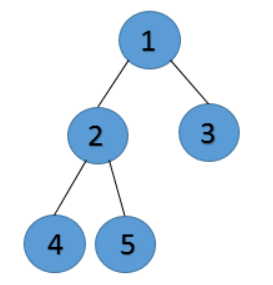
1.先序输入
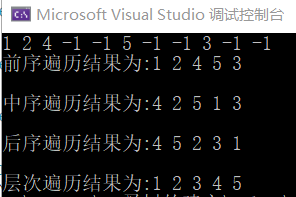
2.层次输入