消消乐

• 问题需求讲解

　　其实第一次写简单的消消乐的代码，是在N多年前入职后的一次新员工的编码比赛上，因为当时允许C++，让我不得不重新翻了几遍丢到角落好多年的《谭浩强C++》。消消乐的需求非常直观明了，每个消消乐的游戏规则或许都有差异，但是不变的是，都是对相同类型的栅格先进行聚合，再判定是否需要进行消除。假设有如下9宫格：

那么首先就需要找出红线区域内的聚合区域。因为我们专题是染色算法，所以重点讲解如何通过染色算法求得聚合区域。

问题简述为：
在nxm的图内，求所有同类型的栅格的聚合区域。

输入：int[]

每个栅格int值表示不同类型。 

输出:List<List<int>>

每个int值表示索引号

• 算法讲解

　　要求得聚合区域，其实就是找寻一个栅格周围4格子是否和其一个类型，如果一个类型，那么再找这个栅格的周围4个格子，直到

　　　　1，当前栅格是已经遍历过的

　　　　2，当前格子不是同样类型的

　　　从第一个栅格开始，按这种逻辑进行聚合。再看第二个栅格是否是已遍历过的，如果不是，那么继续按第二个栅格进行聚合，直到所有栅格都遍历过。那么就可以得到一个各个区域都聚合完毕的集合。如下图：

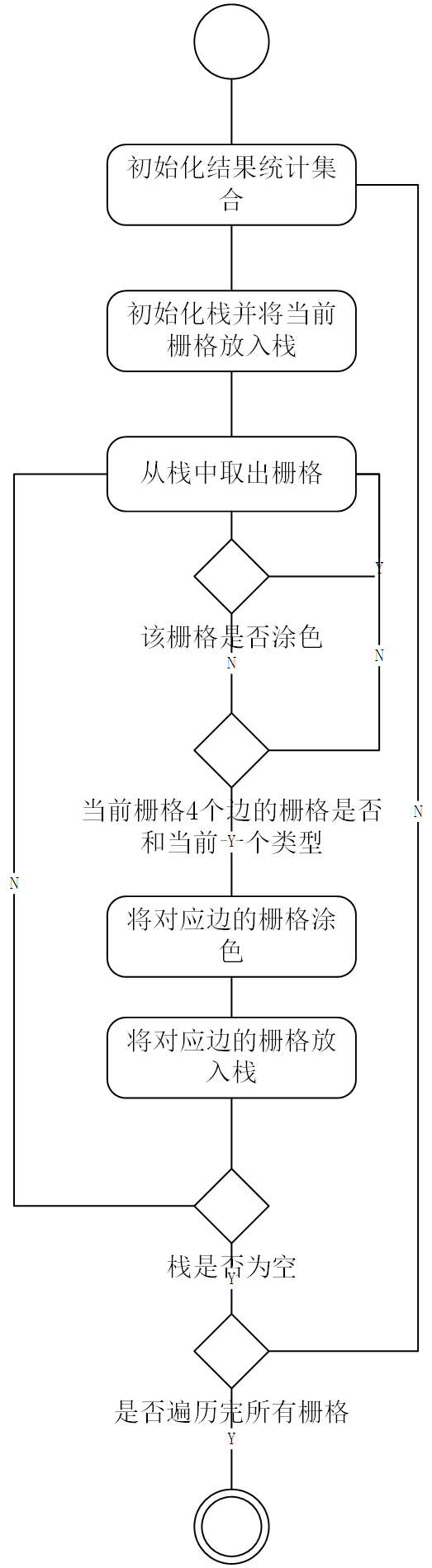
算法流程图如下：

•  代码展示

 public static List<List<int>> GatherGrids(int[] map,int height,int width)
        {
            var l = map.Length;
            var color = new bool[l];
            var result=new List<List<int>>();

            for (int i = 0; i < height; i++)
            {
                for (int j = 0; j < width; j++)
                {
                    if (color[i*width + j])
                    {
                        continue;
                    }

                    var region = new List<int>();
                    Stack<int> stack=new Stack<int>();
                    stack.Push(i*width + j);

                    while (stack.Count>0)
                    {
                        var index = stack.Pop();

                        if (color[index])
                        {
                            continue;
                        }

                        region.Add(index);
                        color[index] = true;
                        var style = map[index];

                        if (index% width != 0)
                        {
                            GatherNextStep(map, index - 1, l, color, style, stack);
                        }

                        if (index% width != width - 1)
                        {
                            GatherNextStep(map, index + 1, l, color, style, stack);
                        }
                        GatherNextStep(map, index-width, l, color, style, stack);
                        GatherNextStep(map, index+width, l, color, style, stack);
                    }

                    result.Add(region);
                }
            }


            return result;
        }

　　没有采用X，Y二维的建模，导致需要做出额外的边界判断，来确保下一步获取的4个方向的Index是正确的。

每次Pop获取当前Index，会首先判断是否已经染过色的索引，防止两个邻居的邻居是同一个栅格，会重复添加。

当然也可以在添加时，判断下栈里是否已经添加。

 private static void GatherNextStep(int[] map, int nextIndex, int l, bool[] color, int style, Stack<int> stack)
        {
            if (IsIndexValid(nextIndex, l) && !color[nextIndex] && map[nextIndex] == style)
            {
                stack.Push(nextIndex);
            }
        }

private static bool IsIndexValid(int index, int l)
        {
            return index >= 0 && index < l;
        }

越界合理性判断。

代码已放入GitHub欢迎pull，欢迎指出bug。

https://github.com/suriyel/EliminateGame/