【DukeImage】Week_3 Spatial processing

Chapter_3 Intensity Transsformations and Spatial Filtering 灰度变换与空间滤波

Intensity transformation function s = T(r) (size of the neighborhood is 1*1)

Some Basic Intensity Transformation Functions
1.Image Negatives 图像反转
$ s = T(r) = L - 1 - r \( 2.Log Transformations 对数变换 \) s = T(r) = clog(1+r) \( 改进傅里叶频谱的丰富度 ![3.3.PNG-33.6kB][2] 3.Power-Law (Gamma) Transformations 幂定律(伽马)变换 \)s = T(r) = cr^\gamma$
进行对比度增强、丰富画面细节。
许多图像获取打印显示的设备根据该定律产生响应，而用于校正这些响应现象的处理则称为Gamma ccorrection(伽马校正)

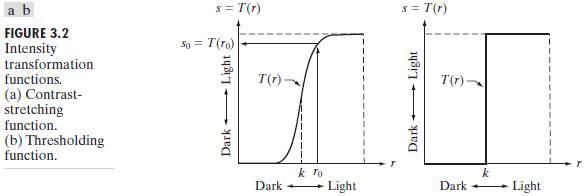
4.Piecewise-Linear Transformation Function 分段线性变换函数
Contrast stretching 对比度拉伸(扩展图像灰度级动态范围)、Intensity-level slicing 灰度级分层(使感兴趣范围灰度级变亮/暗，而保持图像中其他灰度级不变)、Bit-plane slicing 比特平面分层(分析比特、图像压缩)

3.3 Histogram Processing直方图处理
an image whose pixels tend to occupy the entire range of possible intensity levels and, in addition, tend to be distributed uniformly, will have an appearance of high contrast and will exhibit a large variety of gray tones.一幅图像的像素倾向于占据整个可能的灰度级并且分布均匀，则该图像将呈现高对比度并且展示灰色调的较大变化。最终效果将是一副灰度细节丰富且动态范围较大的图像。
分全局global的和局部local

1、Histogram Equalization 直方图均衡化
原理：
一幅图像的灰度级可看成是区间[0,L-1]内的随机变量，我们用其Probability density function,PDF(概率密度函数)来描绘。令pr(r)和ps(s)分别表示随机变量r和s的概率密度函数，由基本的概率论，编花环后的变量s的PDF可由以下公式得到：
$ P_s(s) = P_r(r)\left|\frac{dr}{ds}\right| \( 在图像处理中特别重要的变换函数如下所示： \) s = T(r) = (L-1)\int_0^rp_r(\omega)d\omega $
等式右边是随机变量r的累积分布函数(CDF)进行去归一化映射到[0,L-1] ，结合Leibniz's rule得到：
$ \frac{ds}{dr} = \frac{dT(r)}{dr} = (L-1)\frac{d}{dr}\left[\int_0^rp_r(\omega)d\omega\right] = (L-1)p_r(r)$
将上式结果带入，并记住概率密度值为正，得到：
$ p_s(s) = p_r(r)\left|\frac{dr}{ds}\right| = p_r(r)\left|\frac{1}{(L-1)p_r(r)}\right| = \frac{1}{L-1}
\quad\quad0\le{s}\le{L-1}$
可见，这是一个均匀概率密度函数。
ps(s)始终是均匀的而且与pr(r)的形式无关。
因为直方图是PDF的近似(离散化了)，而且处理中不允许出现新的灰度级，因此在实际的直方图均衡应用中很少见到完美平坦的直方图。

2、Histogram Matching (Specification) 直方图匹配(规定化)
用于产生特定的直方图的方法。令pr(r)为输入图像PDF，pz(z)是希望输出图像所具有的PDF，直方图规定化过程如下：

\[s_k = T(r_k) = (L-1)\sum\limits_{j=0}^{k}p_r(r_j) = \frac{L-1}{MN}\sum\limits_{j=0}^{k}n_j \quad\quad k = 0,1,2...,L-1 \]

1、计算给定图像的直方图pr(r)，通过上式进行直方图均衡化，将sk四舍五入为[0,L-1]范围内的整数。

\[G(z_q) = (L-1)\sum_{i=0}^{q}p_z(z_i) \]

2、由上式计算变换函数G(z)所有的值，把G(z)的值四舍五入为[0,L-1]范围内的整数，将G(z)的值存储在一张表中。
3、对于每一个值sk，使用存储的G值寻找相应的zq值，使G(zq)最接近sk，并存储从s到z的映射，当映射不唯一时选择最小的值。

---

空间滤波基础

平滑空间滤波器 Smoothing Spatial Filters

Smoothing Spatial Filters are used for blurring and for noise reduction
用于模糊处理和降低噪声。

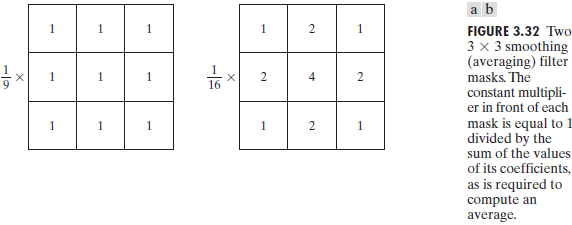
1、Smoothing Linear Filters 平滑线性滤波器

也称为均值滤波器averaging filters。
用滤波器掩模定义的邻域内像素的平均灰度值代替图像中每个像素的值。，从而降低图像灰度尖锐的变化。由于随机噪声通常是灰度级的剧烈变化而形成的，因此平滑处理最显著的应用就是降噪。但是均值滤波器会引起边缘模糊的负面效应。

2、Order-Statistic(Nonlinear) 统计排序(非线性)滤波器
将滤波器包围的图像区域中的像素排序，然后按照排序结果决定的值取代中心像素的值。这一类滤波器中最著名的的是median filter(中值滤波器)。(除此之外比较常用的还有max filter最大值滤波器、min filter最小值滤波器)。

中值滤波器对处理impulse noise (脉冲噪声，也叫做salt-and-pepper nosie 椒盐噪声，以黑白点的形式叠加在图像上) 非常有效。

3、Non Local Means/Averages 非局部平均
NL-Means的全称是：Non-Local Means，直译过来是非局部平均，在2005年由Baudes提出，该算法使用自然图像中普遍存在的冗余信息来去噪声。与常用的双线性滤波、中值滤波等利用图像局部信息来滤波不同的是，它利用了整幅图像来进行去噪，以图像块为单位在图像中寻找相似区域，再对这些区域求平均，能够比较好地去掉图像中存在的高斯噪声。

4、高斯模糊(Gaussian Blur)
也叫高斯平滑，通常用它来减少图像噪声以及降低细节层次。这种模糊技术生成的图像，其视觉效果就像是经过一个半透明屏幕在观察图像，这与镜头焦外成像效果散景以及普通照明阴影中的效果都明显不同。高斯平滑也用于计算机视觉算法中的预先处理阶段，以增强图像在不同比例大小下的图像效果（参见尺度空间表示以及尺度空间实现）。

从数学的角度来看，图像的高斯模糊过程就是图像与正态分布做卷积。由于正态分布又叫作高斯分布，所以这项技术就叫作高斯模糊。图像与圆形方框模糊做卷积将会生成更加精确的焦外成像效果。由于高斯函数的傅立叶变换是另外一个高斯函数，所以高斯模糊对于图像来说就是一个低通滤波器

锐化空间滤波器 Sharpening Spatial Filters
The Principal objective of sharpening is to highlight transitions in intensity
用于突出灰度级过度的部分

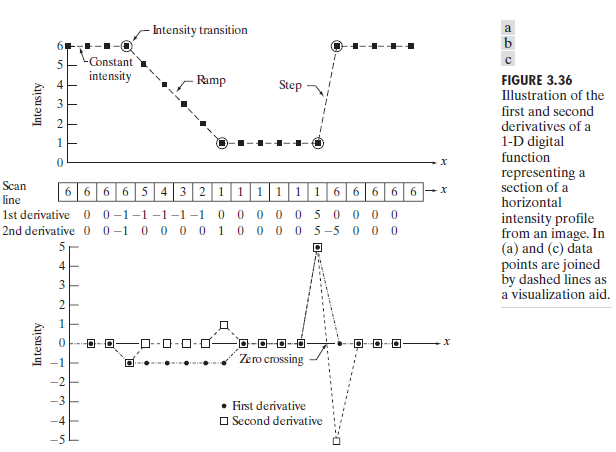
一阶微分和二阶微分的定义如下：
First-order derivative:
$ \frac{\partial f}{\partial x} = f(x+1) - f(x) \( Second-order derivative: \) \frac{\partial^2f}{\partial x^2} = f(x+1) + f(x-1) -2f(x) $

观察上图，注意到一阶微分和二阶微分具有以下性质：
1、both be zero in constant areas 在恒定灰度区域一阶微分和二阶微分都是零
2、first derivative must be nonzero at the onset of an intensity step or ramp 一阶微分在台阶起点或者斜坡起点处不为零
second derivative must be nonzero at the onset and end of an intensity step or ramp 二阶微分在台阶和斜坡的起点以及终点都不为零
3、first derivative must be nonzero along ramps 一阶微分在斜坡上不为零
second derivative must be zero along ramps of constant slope 二阶微分在斜坡上为零

数字图像的边缘在灰度值上通常就是这种斜坡式的过渡。这样就导致图像的一阶微分产生较粗的边缘，因为沿斜坡的微分非零。另一方面，二阶微分则产生一个由零值分开的单像素宽的双边缘。由此得出结论，二阶微分在增强图像细节方面比一阶微分要好很多，这个特性非常适合锐化图像。而且，二阶微分比一阶微分更容易实现，所以我们要更加关注二阶微分。

Using the Second Derivative for Image Sharpening--The Laplacian 用二阶微分进行图像锐化--拉普拉斯算子

一个二维图像的Laplacian定义为
$ \nabla^2f = \frac{\partial^2f}{\partial x^{2}+\frac{\partial}2f}{\partial y^2} $
使用3.6-2的定义，在双变量的情况下，我们得到：
$ \frac{\partial^2f}{\partial x^2} = f(x+1,y) + f(x-1,y)-2f(x,y) \( \) \frac{\partial^2f}{\partial y^2} = f(x,y+1) + f(x,y-1)-2f(x,y) \( 由以上三式，得到双变量的离散拉普拉斯算子为： \) \nabla^2f(x,y) = f(x+1,y) + f(x-1,y) +f(x,y+1)+ f(x,y-1) - 4f(x,y) $
该公式可以用图3.37(a)的滤波模板来实现：

Laplacian是一个微分算子，它强调图像中灰度级的突变，并不强调灰度级缓慢变化的区域，这将产生把灰色边缘线和突变点添加到暗色无特征背景中的图像。将拉普拉斯图像叠加到原图像叠上可以复原背景的特性并保持锐化的效果。

另外，记住拉普拉斯用定义是很重要的，如果定义中使用的是负的中心系数，那么我们就从原图像中减去拉普拉斯图像，而不是加上它。从而得到锐化的结果(增强灰度图突变处的对比度，增强图片细节)。所以，我们使用拉普拉斯对图像增强的基本方法可以表示为下式：
$ g(x,y) = f(x,y) + c\left[\nabla^2f(x,y)\right] $

3.6.3 Unsharp Masking and Highboost Filtering 反锐化掩模和高提升滤波

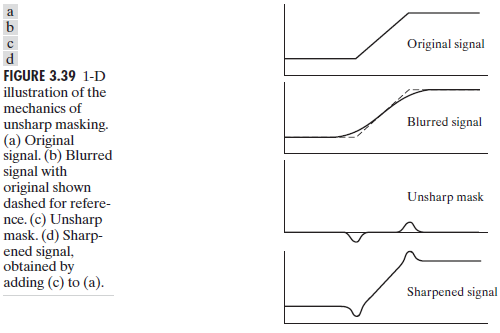
在印刷界和出版界使用多年的锐化图像的方法是，从原图像中减去非锐化(平滑过的)的版本。这种过程称之为unsharp masking反锐化掩模，包括以下过程：
1、Blur the original image. 模糊原图像
2、Substract the blurred image from the original (the resulting difference is called the mask). 从原图像上减去模糊的图像(产生的差值图像称为模板)
3、 Add the mask to the original. 将模板加到原图像上

令$ \hat{f}(x,y) $表示模糊图像，反锐化掩模用公式形式表示如下：
1、首先得到模板 $ g_{mask}(x,y) = f(x,y) - \hat{f}(x,y) \( 2、然后在原图像上加上该模板的一个权重部分\) g(x,y) = f(x,y) + k * gmask(x,y) $ , k称为权重系数。当k=1时，我们得到上面定义的反锐化掩模。当k>1时，该处理称为highboost filtering(高提升滤波)。当k<1时则不强调反锐化掩模的贡献。

Figure 3.39 explains how unsharp masking works.

3.6.4 Using First-Order Derivatives for (Nonlinear) Image Sharpening--The Gradient 用一阶微分对(非线性)图像锐化--梯度

图像处理中的一阶微分使用梯度幅度来实现的。对于函数f(x,y),f在坐标(x,y)处的梯度定义为二维列向量

\[\nabla{f} \equiv grad(f) \equiv \begin{bmatrix}g_x\\g_y\end{bmatrix} = \begin{bmatrix}{\frac{\partial{f}}{\partial{x}} }\\{\frac{\partial{f}} {\partial{y}}}\end{bmatrix} \]

该向量指出了在(x,y)处f的最大变化率的方向。
该向量的幅度值(长度)表示为M(x,y),即
$ M(x,y) = mag(\nabla{f}) = \sqrt{g_x^2+g_y2} $
M是梯度向量在(x,y)处的值(沿梯度方向)。注意，M(x,y)是与原图像大小相同的图像，该图像通常被称为梯度图像(当含义很清楚时可简称为梯度)。

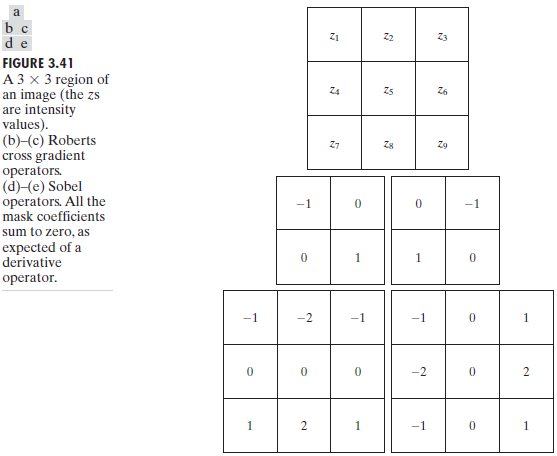
索贝尔算子(Sobel operator)
主要用作边缘检测。在技术上，它是一离散性差分算子，用来运算图像亮度函数的梯度之近似值。在图像的任何一点使用此算子，将会产生对应的梯度矢量或是其法矢量。

MATLAB：

Demo - Enhancement Histogram modification

#读取图像
>> I = imread('tire,tif');
#展示直方图
>> imhist(I);
#反色
>> imshow(255-I);
#直方图均衡化
>> histeq(I);                 

Demo - Median filter

#读取图像
>> I = imread('eight.tif');                                       #加椒盐噪声                   
>> J = imnoise(I, 'salt & pepper', 0.09);                          #中值滤波器        
>> K = medfilt2(J);                                                #展示对比图像                       
>> figure, imshow(I); figure, imshow(I), figure, imshow(K)  

Demo - Unsharp masking

>> I = imread('eight.tif');
>> J = imnoise(I, 'salt & pepper', 0.09);
>> K = medfilt2(J);
#直方图拉伸便于更好的展示边缘
>> figure, imshow(I); figure, imshow(J), figure, imshow(K),figure,imshow(I-K), figure, imshow((I-k).^(2));