上期回顾
上期我从树型结构谈到了红黑树的概念以及自平衡的各种变化(指路上期←戳),本期我将会对TreeMap结合红黑树理论进行解读。
首先,我们先来回忆一下红黑树的5条基本规则。
1.结点是红色或者黑色,
2.根结点为黑色,
3.每个叶子结点都是黑色的空结点,
4.每个红色结点的两个子结点都是黑色,
5.从任何一个结点到叶子结点的所有路径的黑色结点的个数相同。
TreeMap的基本结构
我们先来看一下TreeMap的成员属性,
1 private final Comparator<? super K> comparator; 2 private transient Entry<K,V> root; 3 private transient int size = 0; 4 private transient int modCount = 0;
第1行,比较器,主要是用来维持树结构的有序,可以为空,如果为空,那按照key的自然规则进行排序,
第2行,Entry的引用root,是树型结构的根,
第3行,记录map中数据元素的个数,
第4行,记录map中数据更新的次数,
Entry是TreeMap的一个静态内部类,一个Entry对应一个树型结构中的结点,下面我们来看一下Entry的成员属性和构造函数,
1 static final class Entry<K,V> implements Map.Entry<K,V> { 2 K key; 3 V value; 4 Entry<K,V> left; 5 Entry<K,V> right; 6 Entry<K,V> parent; 7 boolean color = BLACK; 8 9 Entry(K key, V value, Entry<K,V> parent) { 10 this.key = key; 11 this.value = value; 12 this.parent = parent; 13 }
第2行,键
第3行,值
第4行,左结点的引用
第5行,右结点的引用
第6行,父结点的引用
第7行,当前结点默认为黑色结点
第9行,构造函数。初始化键、值、父结点引用
红黑树中的第1条规则是结点是红色或者黑色,在TreeMap中声明了两个常量表示
1 private static final boolean RED = false; 2 private static final boolean BLACK = true;
false表示红色,true表示黑色,根结点是黑色,因此是true。
TreeMap的put方法解读
下面我们解读一下map在新增元素时发生哪些动作?我们以一个public修饰的静态方法,返回值为void,参数为String数组的main方法
作为程序的切入口,如下一段代码,
1 public static void main(String[] args) { 2 TreeMap<Integer, Integer> map = new TreeMap<Integer, Integer>(); 3 map.put(50,3001); 4 map.put(30,3002); 5 map.put(70,3003); 6 }
第2行,new TreeMap<Integer, Integer>(),是一个无参的构造函数,初始化比较器为null,
第3行,新增一个键为50,值为3001的元素,
我们来跟一下put方法,源代码如下,
1 public V put(K key, V value) { 2 Entry<K,V> t = root; 3 if (t == null) { 4 compare(key, key); // type (and possibly null) check 5 6 root = new Entry<>(key, value, null); 7 size = 1; 8 modCount++; 9 return null; 10 } 11 int cmp; 12 Entry<K,V> parent; 13 // split comparator and comparable paths 14 Comparator<? super K> cpr = comparator; 15 if (cpr != null) { 16 do { 17 parent = t; 18 cmp = cpr.compare(key, t.key); 19 if (cmp < 0) 20 t = t.left; 21 else if (cmp > 0) 22 t = t.right; 23 else 24 return t.setValue(value); 25 } while (t != null); 26 } 27 else { 28 if (key == null) 29 throw new NullPointerException(); 30 @SuppressWarnings("unchecked") 31 Comparable<? super K> k = (Comparable<? super K>) key; 32 do { 33 parent = t; 34 cmp = k.compareTo(t.key); 35 if (cmp < 0) 36 t = t.left; 37 else if (cmp > 0) 38 t = t.right; 39 else 40 return t.setValue(value); 41 } while (t != null); 42 } 43 Entry<K,V> e = new Entry<>(key, value, parent); 44 if (cmp < 0) 45 parent.left = e; 46 else 47 parent.right = e; 48 fixAfterInsertion(e); 49 size++; 50 modCount++; 51 return null; 52 }
第2行,把变量t指向根结点的引用,
第3行,判断根结点是否为空,如果为空说明,当前数据元素时首次新增,
第4行,调用自定义的比较器或者自然比较器,自身与自身做比较,旨在判断key是否是null,如果为空,则抛出NPE,
因此,TreeMap中的Key不允许为空。
第6-9行,把root引用指向当前元素,并且树结构的数量size更新为1,modCount自增,结束,返回值为null,
第11行,声明一个int类型的cmp,用来记录比较器的返回值
第12行,声明一个Entry类型的parent,用来记录待存储元素的父结点。上面Entry的构造函数中,其中一个数据项就是父结点,
第15行-26行,当比较器不为空时,找出待存储元素的父结点,下面我们来逐行阅读
第18行,根据我们自定义的比较规则,待存储元素的键和当前结点比较大小,
第19行,如果小于当前结点的键,那么下一个比较的目标应在在左子树上,
第21行,如果大于当前结点的键,那么下一个比较的目标应该在右子树上,
第24行,如果待存储的键等于当前结点的键,那么将新值更新,同时返回旧值。
第27行-42行,当比较器为空时,采用默认的自然比较规则,找出父结点上述基本相似,
注意:第28行,对key是否为空校验,因此:TreeMap中的Key不允许为空。
第43行,赋值,
第44行-47行,确定新增元素时父结点的左结点还是右结点。
第49行-50行,size和modCount分别自增,
接下来我们着来分析第48行,fixAfterInsertion(e),跟一下代码,
1 private void fixAfterInsertion(Entry<K,V> x) { 2 x.color = RED; 3 4 while (x != null && x != root && x.parent.color == RED) { 5 if (parentOf(x) == leftOf(parentOf(parentOf(x)))) { 6 Entry<K,V> y = rightOf(parentOf(parentOf(x))); 7 if (colorOf(y) == RED) { 8 setColor(parentOf(x), BLACK); 9 setColor(y, BLACK); 10 setColor(parentOf(parentOf(x)), RED); 11 x = parentOf(parentOf(x)); 12 } else { 13 if (x == rightOf(parentOf(x))) { 14 x = parentOf(x); 15 rotateLeft(x); 16 } 17 setColor(parentOf(x), BLACK); 18 setColor(parentOf(parentOf(x)), RED); 19 rotateRight(parentOf(parentOf(x))); 20 } 21 } else { 22 Entry<K,V> y = leftOf(parentOf(parentOf(x))); 23 if (colorOf(y) == RED) { 24 setColor(parentOf(x), BLACK); 25 setColor(y, BLACK); 26 setColor(parentOf(parentOf(x)), RED); 27 x = parentOf(parentOf(x)); 28 } else { 29 if (x == leftOf(parentOf(x))) { 30 x = parentOf(x); 31 rotateRight(x); 32 } 33 setColor(parentOf(x), BLACK); 34 setColor(parentOf(parentOf(x)), RED); 35 rotateLeft(parentOf(parentOf(x))); 36 } 37 } 38 } 39 root.color = BLACK; 40 }
fixAfterInsertion,方法名直译过来就是插入之后做调整之意,
第2行,将新元素的结点置为红色,
第4行-38行,调整的过程。
第39行,将调整后的树结构的根置为黑色
下面我们着重来分析第4-38行代码,
第5行→①x的父结点等于x的父结点的父结点的左结点 → x的父结点 是 x父结点的父结点的左结点,
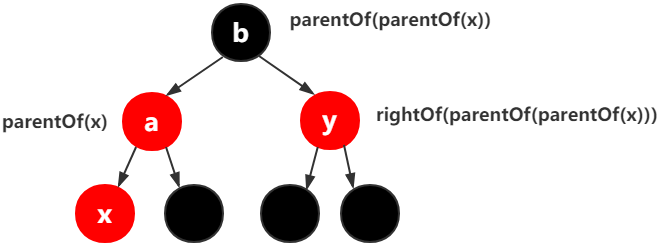
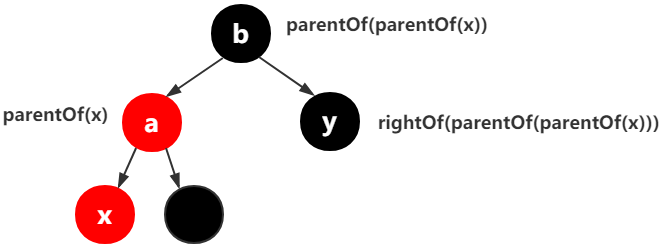
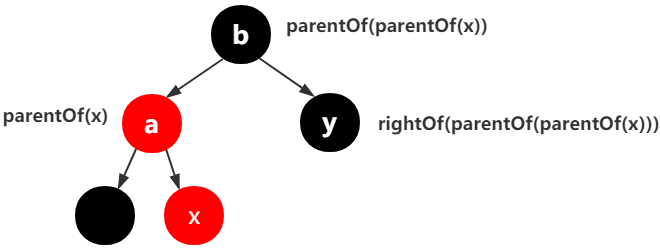
以上3张图都符合,x的父结点是a,a的父结点是b,所以parentOf(x) == leftOf(parentOf(parentOf(x)))
用一句话来描述就是,x的父结点a是a的父结点的左孩子。
第6行,rightOf(parentOf(parentOf(x))),x的父结点的父结点的右结点,记作y,
第7行,如果y为红色,把y变成黑色,把a变成黑色,把b变为红色(如下图所示),同时把x引用指向x的父结点的父结点也就是b结点,本次循环结束,继续下一轮的循环调整。
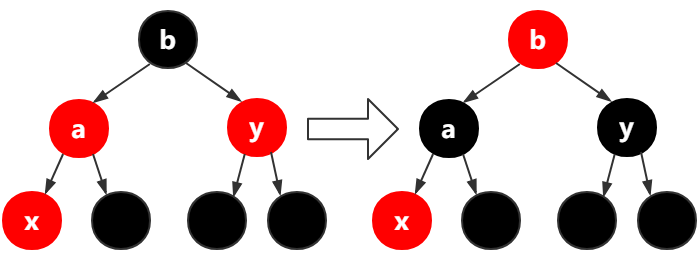
第7行,如果y是黑色,
如果x是结点的右结点,左旋转a(第13行-15行)此时x的引用指向了a,
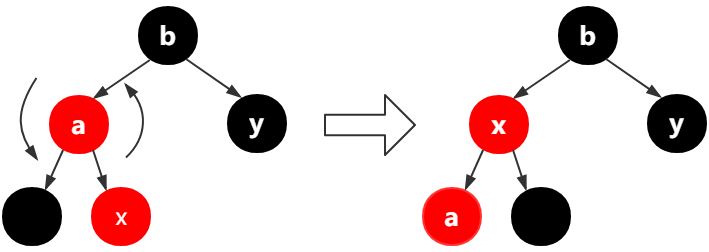
第33行-35行,x(图中的a,因为x引用指向了a)的父结点(图中的x)变为黑色,x父结点(图中的a)的父结点变为红色,对x的父结点的父结点(图中的b)进行右旋
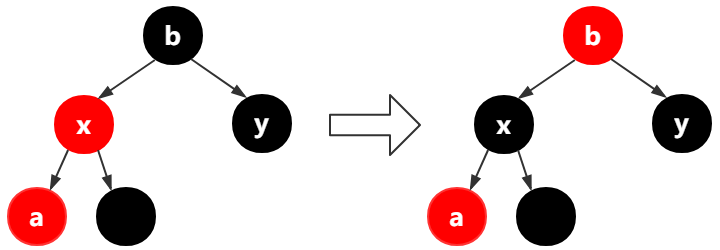
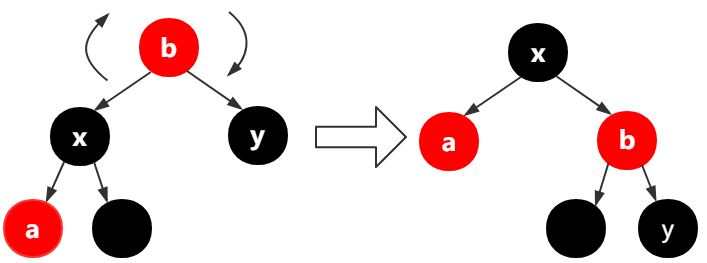
第7行,如果y是黑色,
如果x不是结点的右结点,【左旋转a(第13行-15行)此时x的引用指向了a】,把x的父结点变为黑色,把x的父结点的父结点变为红色,最后将x的父结点的父结点右旋
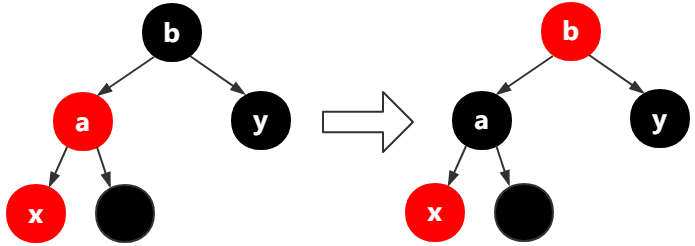
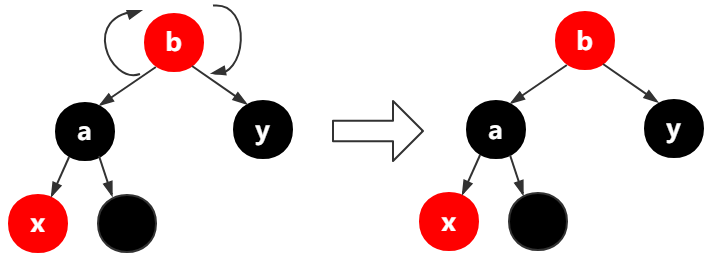
当前分支结束。
下面我们重新回到第5行,
第5行→②x的父结点 不是 x父结点的父结点的左结点,换一句话说就是,
x的父结点 是 x父结点的父结点的右结点,和上述情况比较类似,我们来看一组示意图,
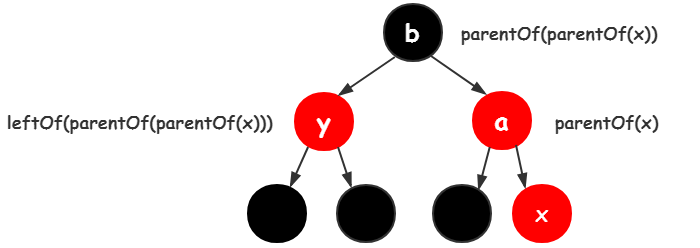
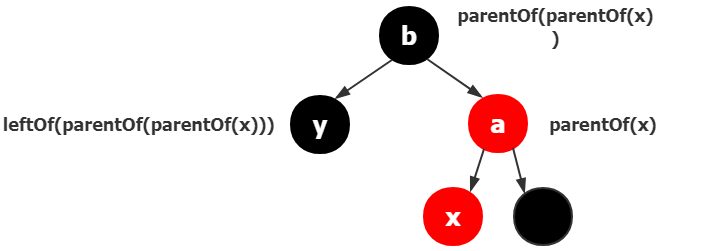
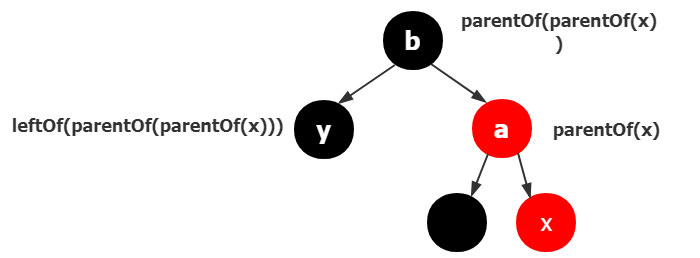
以上3张图都符合,x的父结点是a,a的父结点是b,所以parentOf(x) == rightOf(parentOf(parentOf(x)))
用一句话来描述就是,x的父结点a是a的父结点的右孩子。
第22行,leftOf(parentOf(parentOf(x))),x的父结点的父结点的左结点,记作y,
第23行,如果y为红色,把y变成黑色,把a变成黑色,把b变为红色(如下图所示),同时把x引用指向x的父结点的父结点也就是b结点,本次循环结束,继续下一轮的循环调整。
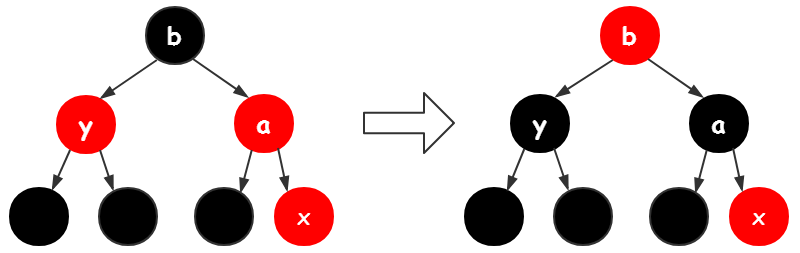
第23行,如果y是黑色,
如果x是结点的左结点,右旋转a(第29行-32行)此时x的引用指向了a,
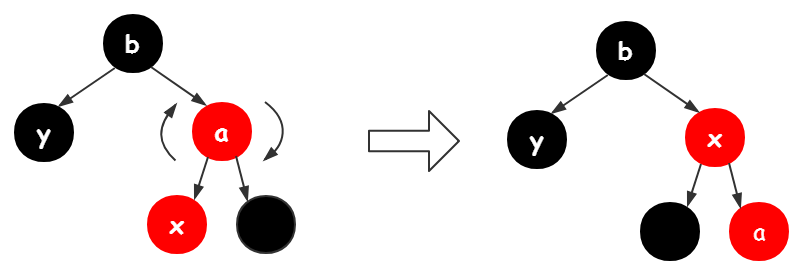
第33行-35行,x(图中的a,因为x引用指向了a)的父结点(图中的x)变为黑色,x父结点(图中的a)的父结点变为红色,对x的父结点的父结点(图中的b)进行右旋
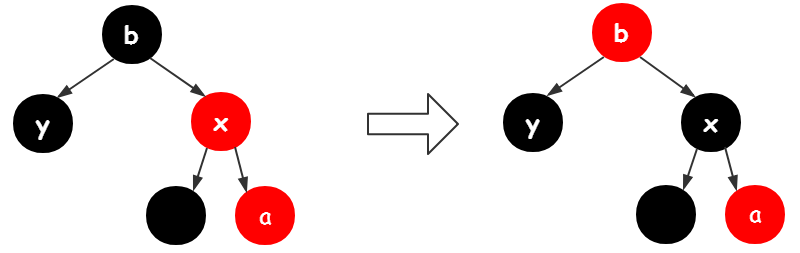
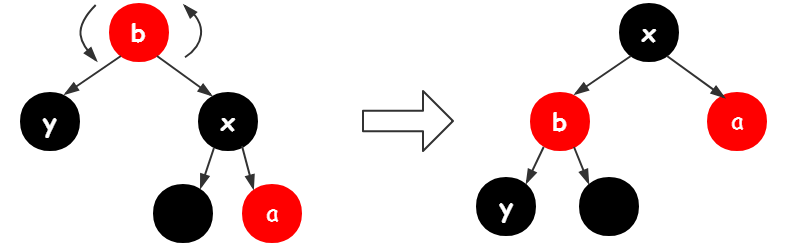
当前分支结束,进入下一轮循环。
以上是对于TreeMap的put方法的解读,比较复杂。下面我简单总结一下fixAfterInsertion的过程
第1步,将新增的元素x置为红色,
第2步,判断新增元素x不为空,且不是root结点,且x的父结点是红色,如果满足,进入第3步,如果不满足跳到第16步,
第3步,判断x的父结点a是否是a的父结点的左结点,如果是,进入第4步,如果不是进入10步,
第4步,取出x父结点的父结点的右结点,记作y,
第5步,判断y的颜色是否为红色,如果是,进入第6步,如果不是进入7步,
第6步,x的父结点置为黑色,x父结点的父结点的右结点,即y置为黑色,x的父结点的父结点置为红色,x的引用指向x的父结点的父结点,跳到第2步,
第7步,判断x是否是x父结点的右结点,如果是,进入第8步,如果不是,进入第9步,
第8步,x的应用指向x的父结点,x左旋(注意,此时x指向的是原x的父结点)
第9步,x的父结点置为黑色,x的父结点的父结点置为红色,x的父结点的父结点右旋,跳到第2步,
第10步,取出x父结点的父结点的左结点,记作y,
第11步,判断y的颜色是否为红色,如果是,进入第12步,如果不是进入13步,
第12步,x的父结点置为黑色,x父结点的父结点的左结点,即y置为黑色,x的父结点的父结点置为红色,x的引用指向x的父结点的父结点,跳到第2步,
第13步,判断x是否是x父结点的左结点,如果是,进入第14步,如果不是,进入第15步,
第14步,x的引用指向x的父结点,x右旋(注意,此时x指向的是原x的父结点)
第15步,x的父结点置为黑色,x的父结点的父结点置为红色,x的父结点的父结点左旋,跳到第2步,
第16步,把根节点置为黑色。
由于内容较多,因此TreeMap源码解析分为上篇、中篇和下篇3部分,
下期预告
1 TreeMap<Integer, Integer> map = new TreeMap<Integer, Integer>(); 2 map.put(50,3001); 3 map.put(30,3002); 4 map.put(70,3003);
本文提到的简单例子的树我们还没有建立起来,由于内容较多,所以打算,把这一部分也放在【java集合之TreeMap源码解析中篇】来讲解。谢谢关注。