The Stern-Brocot tree is an infinite complete binary tree in which the vertices correspond one-for-one to the positive rational numbers, whose values are ordered from the left to the right as in a search tree.
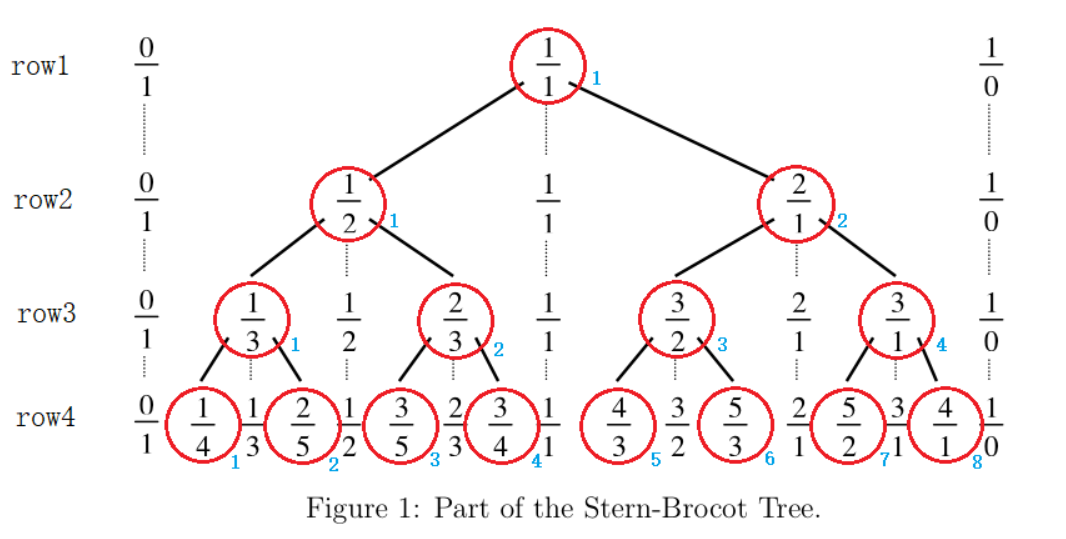
Figure 1 shows a part of the Stern-Brocot tree, which has the first 4 rows. Each node in the tree is marked in a red cycle. The value in the node is the mediant of the left and right fractions. The mediant of two fractions A/B and C/D is defined as (A+C)/(B+D).
To construct the Stern-Brocot tree, we first define the left fraction of the root node is 0/1, and the right fraction of the root node is 1/0. So the value in the root node is the mediant of 0/1 and 1/0, which is (0+1)/(1+0)=1/1. Then the value of root node becomes the right fraction of the left child, and the left fraction of the right child. For example, the 1st node in row2 has 0/1 as its left fraction and 1/1(which is the value of its parent node) as its right fraction. So the value of the 1st node in row2 is (0+1)/(1+1)=1/2. For the same reason, the value of the 2nd node in row2 is (1+1)/(1+0)=2/1. This construction progress goes on infinitly. As a result, every positive rational number can be found on the Stern-Brocot tree, and can be found only once.
Given a rational number in form of P/Q, find the position of P/Q in the Stern-Brocot Tree.
输入描述:
Input consists of two integers, P and Q (1<=P,Q<=1000), which represent the rational number P/Q. We promise P and Q are relatively prime.
输出描述:
Output consists of two integers, R and C.
R indicates the row index of P/Q in the Stern-Brocot Tree, C indicates the index of P/Q in the row.
Both R and C are base 1.
We promise the position of P/Q is always in the first 12 rows of the Stern-Brocot tree, which means R<=12.
输入例子1:
5 3
输出例子1:
4 6
思路:
在这里我尝试用递归的方式来实现此功能。
具体而言,要定义一个寻找目标分数位置的函数search:
search(P,Q,X,Y,Row,Col,Lx,Ly,Rx,Ry)
这里的P/Q为要寻找的目标分数,X/Y为 当前已经找到的分数,Row与Col分别为当前找到的分数X/Y所在的位置,Lx/Ly,Rx/Ry分别为要想找到X/Y所用的两个数,即X = Lx+Rx,Y = Ly+Ry。
当向左搜索时:
X(i+1)=X(i)+Lx(i),Y(i+1)=Y(i)+Ly(i),Row(i+1)=Row(i)+1,Col(i+1)=2*Col(i)-1,Lx(i+1)=Lx(i),Ly(i+1)=Ly(i),Rx(i+1)=X(i),Ry(i+1)=Y(i)
当向右搜索时:
X(i+1)=X(i)+Rx(i),Y(i+1)=Y(i)+Ry(i),Row(i+1)=Row(i)+1,Col(i+1)=2*Col(i),Lx(i+1)=X(i),Ly(i+1)=Y(i),Rx(i+1)=Rx(i),Ry(i+1)=Ry(i)
由此我们可以写出代码如下:
def search(P,Q,X,Y,Row,Col,Lx,Ly,Rx,Ry): #终止条件 if P==X and Q==Y: return Row,Col #向左搜索 if P/Q < X/Y: r,c = search(P,Q,X+Lx,Y+Ly,Row+1,2*Col-1,Lx,Ly,X,Y) return r,c #向右搜索 if P/Q > X/Y: r,c = search(P,Q,X+Rx,Y+Ry,Row+1,2*Col,X,Y,Rx,Ry) return r,c getNumFromString = lambda x:list(map(int,x.strip().split())) p,q = getNumFromString(input()) R,C = search(p,q,1,1,1,1,0,1,1,0) print(R,C)