数据结构与算法基础
数组与矩阵
数组类型 存储地址计算
一维数组 a[i]的存储地址为:a+i*len
a[n]
二维数组 a[m][n] a[i][j]的存储地址 (按行存储) 为:a+(i*n+j)*len
a[i][j]的存储地址 (按列存储) 为:a+(j*m+i)*len
练习1:
已知5行5列的二维数组a中的各元素占两个字节,求元素a[2][3]按行优先存储的存储地址?

答:a+26 根据按行存储:a+(i*n+j)*len
稀疏矩阵
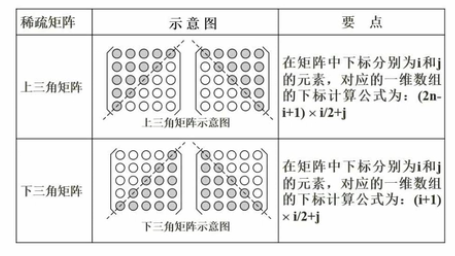
上三角矩阵:(2n-i+1)*i/2+j
下三角矩阵:(i+1)*i/2+j
考试快捷方法:代入法
练习1:


将A00 代入,i=0,j=0,A选项为1,B选项为0,C选项为0,D选项为1 排除B C 代入A11,为3则是正确答案
数据结构的定义
数据逻辑结构
1.线性结构
2.非线性结构
树状图、图
线性表
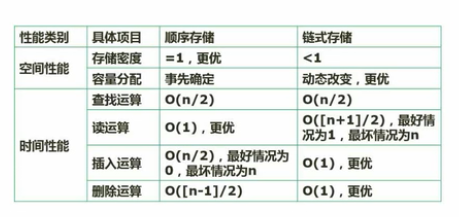
线性表存储方式
顺序表:连续方式,类似一维数组
链表:存数据、存指针
链表的基本操作:
① 单链表删除结点
② 单链表插入结点
③ 双向链表删除结点
④ 双向链表插入结点
顺序存储与链式存储对比
队列与栈
队列:先进先出
栈:先进后出
循环队列:
队空条件:head=tail
队满条件:(tail+1)%size=head
练习1:
元素按照a、b、c的次序进入栈,请尝试写出其所有可能的出栈序列

答:a b c
b a c
c b a
练习2:
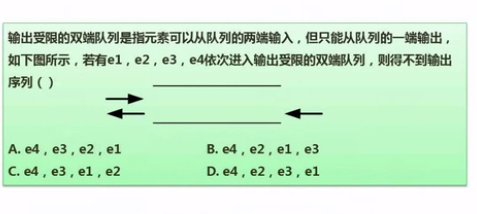

答:D
广义表
表头(head):第一个元素 表尾(tail):除了表头以外的所有元素


例1: LS1长度为:3,深度为(嵌套次数):2,深度就是包括括号的层数 例2: head(tail(LS1))得到 (b,c) head(head(tail(LS1)))得到 b
树与二叉树
结点的度:一个结点拥有的孩子结点数
树的度:结点最高的度
叶子结点:没有孩子节点的
分支结点:有相应的分支
内部结点:既非叶子结点,也非根节点,夹在中间
父结点:有子结点
子结点:
兄弟结点:平级结点
层次结点:分层次
二叉树的重要性
1.在二叉树的第i层上最多有2的i-1次方个结点(i>=1);
2.深度为k的二叉树最多有2的k次方-1个结点(i>=1);
3.对任何一个二叉树,如果其叶子结点数为n0,度为2的结点数为n2,则n0=n2+1;
二叉树遍历
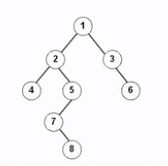
前序遍历:根左右(1 2 4 5 7 8 3 6)
中序遍历:左根右(4 2 7 8 5 1 3 6)
后序遍历: 左右根(4 8 7 5 2 6 3 1)
层次遍历:依次遍历
哈夫曼树
基本概念
树的路径长度:树中路径累加长度
权:数值代表某种字符出现的频度
带权路径长度:路径长度*权值
树的带权路径长度:总的带权路径长度相加
排序与查找
算法基础及常见的算法
算法的特点:
有穷性:执行有穷步之后结束
确定性:算法中每一条指令都必须有确切的含义,不能含糊不清
输入(>=0)
输出(>=1)
有效性:算法的每个步骤都能有效执行并能得到确定的结果,例如a=0,b/a就无效
算法的复杂度:

顺序查找:

等概率:(n+1)/2
二分查找法:

(注:有序排列)
散列表查找:
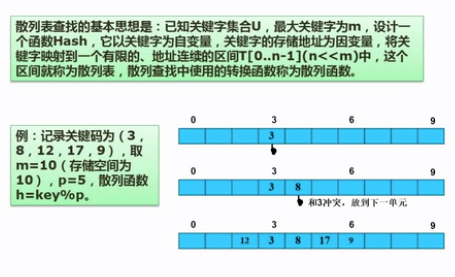
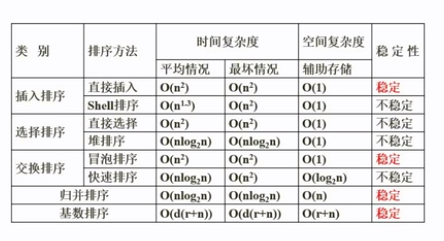
排序方法分类
① 插入类排序
直接插入排序
直接选择排序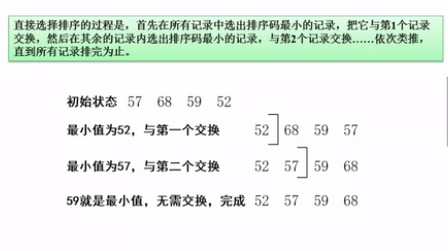
希尔排序
(注:取奇数排序)
② 交换类排序
冒泡排序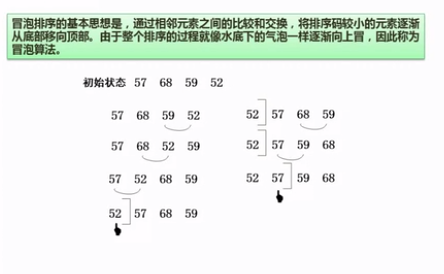
快速排序
③ 选择类排序
简单选择排序
堆排序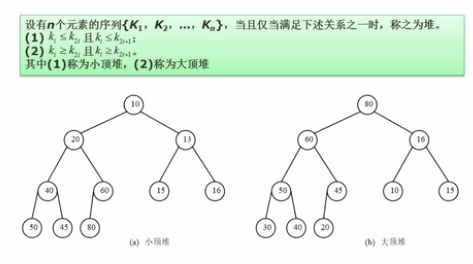

④ 归并排序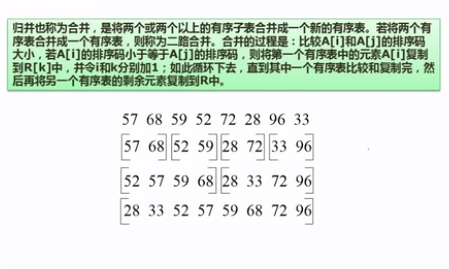
⑤ 基数排序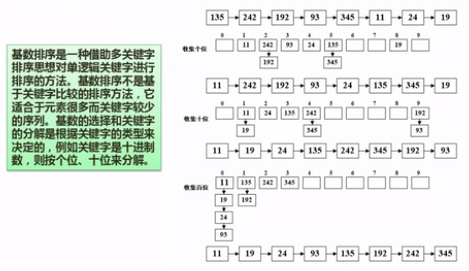
排序状况