Booksort
Time Limit: 10000/10000 MS (Java/Others) Memory Limit: 102400/102400 K (Java/Others)
Total Submission(s): 173 Accepted Submission(s): 81
Problem Description
The Leiden University Library has millions of books. When a student wants to borrow a certain book, he usually submits an online loan form. If the book is available, then the next day the student can go and get it at the loan counter. This is the modern way of borrowing books at the library.
There is one department in the library, full of bookcases, where still the old way of borrowing is in use. Students can simply walk around there, pick out the books they like and, after registration, take them home for at most three weeks.
Quite often, however, it happens that a student takes a book from the shelf, takes a closer look at it, decides that he does not want to read it, and puts it back. Unfortunately, not all students are very careful with this last step. Although each book has a unique identification code, by which the books are sorted in the bookcase, some students put back the books they have considered at the wrong place. They do put it back onto the right shelf. However, not at the right position on the shelf.
Other students use the unique identification code (which they can find in an online catalogue) to find the books they want to borrow. For them, it is important that the books are really sorted on this code. Also for the librarian, it is important that the books are sorted. It makes it much easier to check if perhaps some books are stolen: not borrowed, but yet missing.
Therefore, every week, the librarian makes a round through the department and sorts the books on every shelf. Sorting one shelf is doable, but still quite some work. The librarian has considered several algorithms for it, and decided that the easiest way for him to sort the books on a shelf, is by sorting by transpositions: as long as the books are not sorted,
take out a block of books (a number of books standing next to each other),
shift another block of books from the left or the right of the resulting ‘hole’, into this hole,
and put back the first block of books into the hole left open by the second block.
One such sequence of steps is called a transposition.
The following picture may clarify the steps of the algorithm, where X denotes the first block of books, and Y denotes the second block.
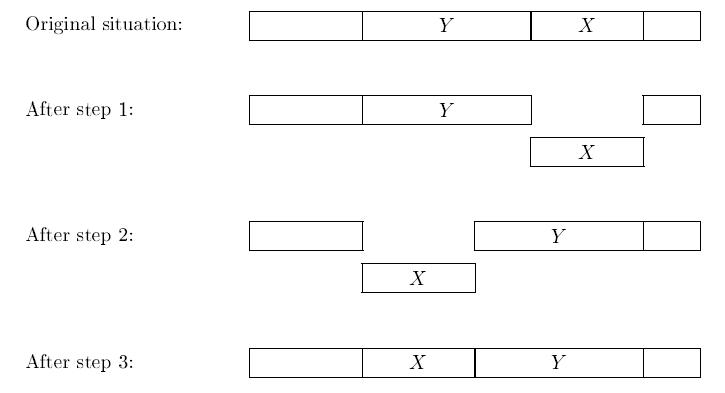
Of course, the librarian wants to minimize the work he has to do. That is, for every bookshelf, he wants to minimize the number of transpositions he must carry out to sort the books. In particular, he wants to know if the books on the shelf can be sorted by at most 4 transpositions. Can you tell him?
There is one department in the library, full of bookcases, where still the old way of borrowing is in use. Students can simply walk around there, pick out the books they like and, after registration, take them home for at most three weeks.
Quite often, however, it happens that a student takes a book from the shelf, takes a closer look at it, decides that he does not want to read it, and puts it back. Unfortunately, not all students are very careful with this last step. Although each book has a unique identification code, by which the books are sorted in the bookcase, some students put back the books they have considered at the wrong place. They do put it back onto the right shelf. However, not at the right position on the shelf.
Other students use the unique identification code (which they can find in an online catalogue) to find the books they want to borrow. For them, it is important that the books are really sorted on this code. Also for the librarian, it is important that the books are sorted. It makes it much easier to check if perhaps some books are stolen: not borrowed, but yet missing.
Therefore, every week, the librarian makes a round through the department and sorts the books on every shelf. Sorting one shelf is doable, but still quite some work. The librarian has considered several algorithms for it, and decided that the easiest way for him to sort the books on a shelf, is by sorting by transpositions: as long as the books are not sorted,
take out a block of books (a number of books standing next to each other),
shift another block of books from the left or the right of the resulting ‘hole’, into this hole,
and put back the first block of books into the hole left open by the second block.
One such sequence of steps is called a transposition.
The following picture may clarify the steps of the algorithm, where X denotes the first block of books, and Y denotes the second block.

Of course, the librarian wants to minimize the work he has to do. That is, for every bookshelf, he wants to minimize the number of transpositions he must carry out to sort the books. In particular, he wants to know if the books on the shelf can be sorted by at most 4 transpositions. Can you tell him?
Input
The first line of the input file contains a single number: the number of test cases to follow. Each test case has the following format:
One line with one integer n with 1 ≤ n ≤ 15: the number of books on a certain shelf.
One line with the n integers 1, 2, …, n in some order, separated by single spaces: the unique identification codes of the n books in their current order on the shelf.
One line with one integer n with 1 ≤ n ≤ 15: the number of books on a certain shelf.
One line with the n integers 1, 2, …, n in some order, separated by single spaces: the unique identification codes of the n books in their current order on the shelf.
Output
For every test case in the input file, the output should contain a single line, containing:
if the minimal number of transpositions to sort the books on their unique identification codes (in increasing order) is T ≤ 4, then this minimal number T;
if at least 5 transpositions are needed to sort the books, then the message "5 or more".
if the minimal number of transpositions to sort the books on their unique identification codes (in increasing order) is T ≤ 4, then this minimal number T;
if at least 5 transpositions are needed to sort the books, then the message "5 or more".
Sample Input
3
6
1 3 4 6 2 5
5
5 4 3 2 1
10
6 8 5 3 4 7 2 9 1 10
Sample Output
2
3
5 or more
Source
题意:
给n本书,编号1-n,乱序的,现在可以任选连续的一摞书插入到任意位置,问能否在4步内使书编号升序。能输出最少步数,不能输出 5 or more。
感想:
虽然深度只有4层,但状态还是太多了,先尝试了一下dbfs,连最后一组都跑不出来,提交果断TLE。后来看了lcm博客发现是IDA*,哎,我的A*基本是空白,看了启发式函数之后才A的。A*很强大,以后要开始研究啦。
思路:
主要是找启发式函数,考虑到每次操作只会影响3个块的后继块是否正确,所以得到启发式函数f(s)=h(s)+3*g(s).黑书上P169有类似讲解,可供参考。
代码:
#include <iostream>
#include <cstdio>
#include <cstring>
#include <queue>
#define maxn 16
using namespace std;
int n,m,ans,depth,flag;
int a[maxn];
bool isok()
{
int i,j;
for(i=1;i<=n;i++)
{
if(a[i]!=i) return false ;
}
return true ;
}
int h()
{
int i,j,t=0;
for(i=0;i<=n;i++)
{
if(a[i]+1!=a[i+1]) t++;
}
return t;
}
void dfs(int d)
{
if(isok())
{
flag=1;
return ;
}
if(flag||(d-1)*3+h()>depth*3) return ; // 实现IDA*
int i,j,k,p;
int tmp[maxn];
for(i=1; i<=n; i++) // 模拟操作
{
for(j=i; j<=n; j++)
{
for(k=1; k<=i-1; k++)
{
memcpy(tmp,a,sizeof(tmp));
for(p=k; p<=i-1; p++)
{
a[p+j-i+1]=tmp[p];
}
for(p=i; p<=j; p++)
{
a[p-i+k]=tmp[p];
}
dfs(d+1);
memcpy(a,tmp,sizeof(tmp));
}
for(k=j+1; k<=n; k++)
{
memcpy(tmp,a,sizeof(tmp));
for(p=j+1; p<=k; p++)
{
a[p-j-1+i]=tmp[p];
}
for(p=i; p<=j; p++)
{
a[p+k-j]=tmp[p];
}
dfs(d+1);
memcpy(a,tmp,sizeof(tmp));
}
}
}
}
int main()
{
int i,j,t,flg;
scanf("%d",&t);
while(t--)
{
scanf("%d",&n);
flg=1;
for(i=1; i<=n; i++)
{
scanf("%d",&a[i]);
if(a[i]!=i) flg=0;
}
a[0]=0,a[n+1]=n+1;
if(flg)
{
printf("0
");
continue ;
}
flag=depth=0;
while(!flag)
{
depth++;
dfs(1);
if(depth>=4) break ;
}
if(flag) printf("%d
",depth);
else printf("5 or more
");
}
return 0;
}