Codeforces 1338 题解

A

对于每个 (i) 我们求出 (b_i) 表示 (i) 这个数最少要增加多少（(max^i_{j=1}a_j-a_i)），答案等于最小的 (k) 使得 $2^{k-1ge max}n_b_i$. 时间复杂度 (O(n)). 代码: 76336034

B

最小：只要存在两个叶子距离为奇数，答案就是 $3$，否则是 $1$. 最大：等于非叶子节点数加上和至少一个叶子节点相连的非叶子节点数 (-1)。显然和同一个点相连的叶子边权必须相等。那么考虑去掉叶子节点后剩下的树，由于你可以安排任意大的数，所以一定能做到边权互不相同。 时间复杂度 (O(n)). 代码: 76352259

C

找规律即可。打表前 $16$ 位不难发现就是先四进制分解，由 (mod 3) 的值得到答案的最高位，剩下的每一位做个置换。 归纳证明应该不难。 听说这个规律还和 nim 积有关。 时间复杂度 (O(log n)). 代码: 76377989

D

我的做法还是找规律（然而脑速太慢赛后搞了一上午）。找规律的过程非常麻烦，实在不太会讲，直接说一下结论好了： 设 (f[u][0/1]) 表示 (u) 点的子树内，被根包含/不被根包含的最大层数。需要 $0/1$ 是因为把根套在外面之后，仅仅能套住那些不被根的儿子包含的圈，而需要和根的儿子相交。这也就意味着，一个子树的状态可以表示为两个相交的圈，其中较大的一个是根，另外一个不是根。 假设 (u) 有若干儿子 (v_1,v_2,...,v_{sonn[u]}). 那么最优方案一定会套成如下所示，蓝色的是 (u)，黑色和红色分别是每个儿子的根 ($0$) 和非根 ($1$). 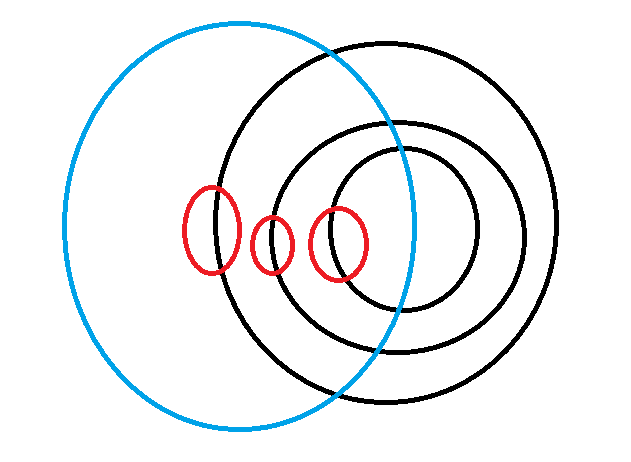于是可以得到这样的方程： (f[u][1]=max_i max(f[v_i][0],f[v_i][1])+(sonn[u]-1)) 再考虑 (f[u][0]) 的转移，显然有 (f[u][0]=max_i f[v_i][1]+1) 换根 dp 即可。 时间复杂度 (O(n)). 比较有道理的做法见 (color{black}{ ext{s}}color{red}{ ext{uwakow}}) 神仙的题解: https://www.cnblogs.com/suwakow/p/12692393.html 代码: 76449398

E

题解: https://www.cnblogs.com/suncongbo/p/12779107.html