注意事项:
1. 只有通过先序和中序 或者 中序和后序,可以还原出原始的二叉树(确定一个二叉树)
2. 已知先后中序的任意一个序列 或者 先序和后序,都不能还原出原始的二叉树
已知先序和中序,求后序:
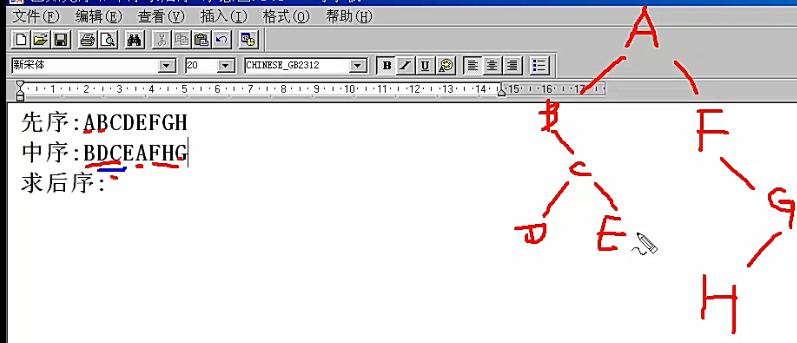
思路:
先序里面,最先出现的是根节点,所以A就是根节点
中序里面,根节点A在中间,所以A的左边BDCE是左子树,A的右边FHG是右子树
先序里面,A的左子树B最先出现,所以B是左子树的根节点
中序里面,根节点B的左边没有结点,所以B的左子树为空,即DCE是B的右子树
先序里面,B的右子树C最先出现,所以C是右子树的根节点
中序里面,D在C的左边,E在C的右边,所以D是C的左子树,E是C的右子树
至此,A的左子树还原完毕
先序里面,A的右子树F最先出现,所以F是根节点
中序里面,根节点F的左边没有结点,所以F的左子树为空,即HG是F的右子树
先序里面,F的右子树G最先出现,所以G是根节点
中序里面,根节点G的左边有结点H,所以H是G的左子树
至此,A的二叉树还原完毕
即原始二叉树的后序为:D-E-C-B-H-G-F-A
已知中序和后序,求先序:

后序里面,最后出现的是根节点,所以A是根节点
中序里面,根节点A在中间,所以A的左边BDCE是左子树,A的右边FHG是右子树
后序里面,A的左子树B最后出现,所以B是左子树的根节点
中序里面,根节点B的左边没有结点,所以B的左子树为空,B的右子树是DCE
后序里面,B的右子树C最后出现,所以C是根节点
中序里面,根节点C的左边是E,所以E是C的左子树,C的右边是E,所以E是C的右子树
至此A的左子树还原完毕
后序里面,A的右子树F最后出现,所以F是根节点
中序里面,根节点F左边没有结点,所以F的左子树为空,F的右子树为HG
后序里面,F的右子树G最后出现,所以G是根节点
中序里面,G的左子树为H,G的右边没有结点,所以G的右子树为空
至此,A的二叉树还原完毕
所以先序为:A-B-C-D-E-F-G-H
通过这两个例子不难发现,已知先序和中序或者中序和后序,进行还原二叉树时需要不断交替观察结点在先序、中序或者中序、后序里的位置,结合先序遍历、中序遍历、后序遍历的特点,根据先序和后序能确定根节点,根据中序能判断左右子树的结点,这样便能还原出原始的二叉树。