欧拉函数及其扩展 小结

一、定义

欧拉函数定理是数论中极其常用的一个定理。对于一个正整数n，它的欧拉函数值φ(n)代表小于n的正整数中与n互质的数的个数。例如，对于n = 9，在小于n的正整数中有1、2、4、5、7、8与9互质，所以φ(9) = 6。

欧拉函数定理给出了计算公式。正整数n的欧拉函数值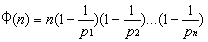，其中，p代表n的第几个质因子。例如，12有两个质因子2、3（注意这里的质因子不能重复计算），所以φ(12) = 12*(1/2)*(2/3) = 4。

二、性质

①若n为质数，显然，φ(n) = n - 1

②若n为奇数，有φ(2 * n) = φ(n)

③对于n > 2，所有的φ(n)均为偶数。

④小于n的与n互质的数的和可以表示为φ(n)*n/2

⑤线性同余方程 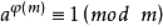恒成立，由此还可以引出费马小定理，即当p为质数时，有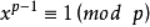。这条性质常被应用于求取乘法逆元。

⑥求取最小的m(m > 1)，使φ(m) >= n，得到的m应为从n + 1开始的第一个素数。此条是我从欧拉函数表中观察得出的，或许有用，可以参考LightOJ1370。

三、计算方法

①从上面的计算公式可以看出，求一个数的欧拉函数值，需要得到它所有的质因子。我们可以借助质因子分解法来完成。原理和细节参见代码。

O(sqrt(n))求取φ(n)

int euler(int n)//求取φ(n)
{
    int re = n;//这里实际上完成了公式中乘n的那一步
    for(int i = 2;i * i <= n;i++)
    {
        if(n % i == 0)//质因子分解，下方的操作保证了i为质数
        {
            re = re / i * (i - 1);//欧拉函数的计算公式，这里先计算除法可以有效地防止溢出
            while(n % i == 0)//从n中约去所有的i，确保下一次得到的i仍为质数
            {
                n /= i;
            }
        }
    }
    if(n != 1)//特殊情况，由于我们将复杂度优化到了O(sqrt(n)）
        re = re / n * (n - 1);//则n在上面的操作中可能被约成了一个质数（或者它本身就是个质数），这里也需要计算在内。
    return re;
}

 ②有时，我们会遇到需要多次查询很多个数的欧拉函数值的情况，O(sqrt(n))可能不够用。这时我们可以结合埃氏素数筛选法，在一趟遍历中通过寻找质数完成n个欧拉函数值的计算，快速地获得欧拉函数表。原理参见代码。

//O(maxn)获取欧拉函数表
int euler_table[maxn + 1];
for(int i = 0;i <= maxn;i++)
{
    euler_table[i] = i;//这里实际上完成了公式中乘n的那一步
}
for(int i = 2;i <= maxn;i++)
{
    if(euler_table[i] == i)//根据埃氏筛法，在下面的处理下，满足这个判断的i一定是质数
    {
        for(int j = i;j <= maxn;j += i)//遍历i所有的倍数
        {
            euler_table[j] = euler_table[j] / i * (i - 1);//对所有i的倍数进行计算，这样，只要遍历了一个数所有的质因子，这个数的欧拉函数值也就得出了。
        }
    }
}

四、扩展欧拉定理

求解同余方程a^b ≡ x(mod m)时，b可能会非常大，扩展欧拉定理可以优化其计算。

当gcd(a, m) == 1时，由上方的性质④可以很容易地得出，a^b ≡ a^(b % φ(m)) (mod m)

当gcd(a, m) > 1 且b  > φ(m)时，a^b ≡ a^(b % φ(m) + φ(m)) (mod m)

推导过程见https://blog.csdn.net/synapse7/article/details/19610361