支持向量机（Support Vector Machine, SVM）
基本思想就是找两类数据的最大间隔。
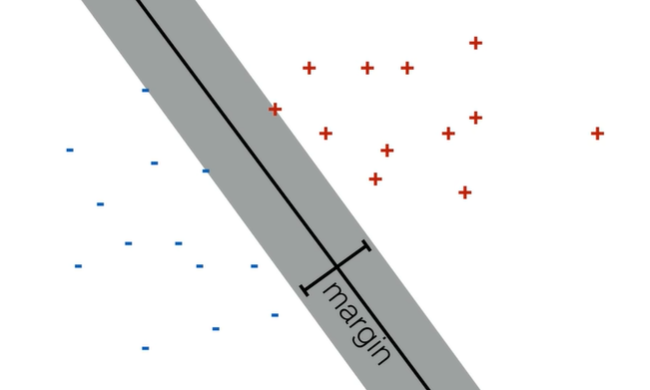
一、目标函数
令数据集为 D，标签 y 为 +1、-1。
正确的分类可以用这个不等式描述：
当我们不希望有点落在边界时，公式改写为：
即将支持向量的函数间隔为 1，相当于对wT 、b 进行了缩放，对超平面的确定并没有影响。
假设左右边距离分界线最近的两个点是 x+ 和 x-，x+ 和 x- 的连线垂直于决策线，所以两点连线的方向是 w 乘一个缩放因子 γ。就有最下面一个公式。
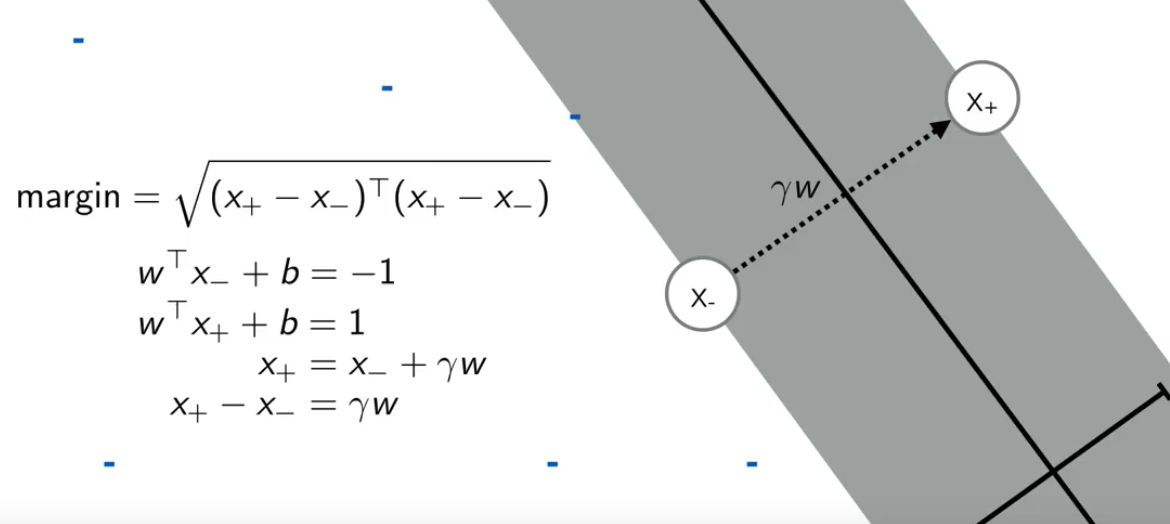
以上公式变形得到：
把γ代回，得到两点的间隔公式：
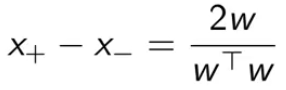
将右边的向量平方再开方计算幅度，得到2除以 w 的二范式
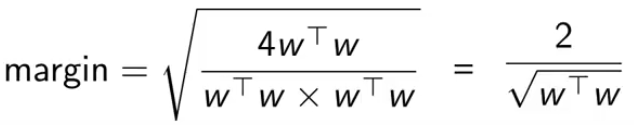
所以优化问题变为最大化 w 的二范式。
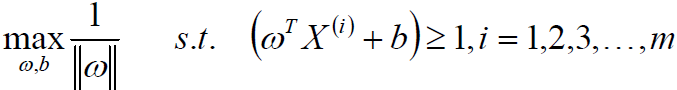
也就是最小化下式（最小化是因为这种形式更加符合优化问题 ），分母2是为了求导方便。
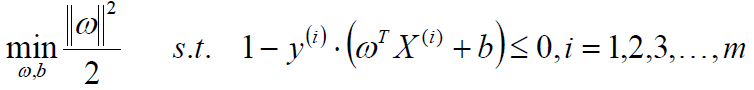
求解的方法有很多：
① 很多工具使用内点法求解
② 梯度下降法。hinge-loss代替约束，求导然后用步长优化。
③ 大多数时候使用对偶函数优化。把约束从目标函数中拿出，换成一个惩罚项来产生优化中的鞍点。（拉格朗日）
以上是两类数据线性可分的情况，对于不完全线性可分，加入松弛变量 ξ。松弛变量中每个元素对应一个样本。这也就是软间隔SVM。
当然，我们不希望 ξ 太大，所以在目标函数中，加入一项 ξ 的惩罚项。C起到了平衡的作用。
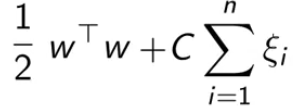
二、对偶问题
大多数优化问题可以从两个角度来看，一个是原问题，一个是对偶问题。解出了对偶问题就等于解出了原问题。
接下来推导拉格朗日（KKT）对偶。
下式是拉格朗日函数，α、β是用来控制两个约束的（分类正确以及ξ 大于0）。
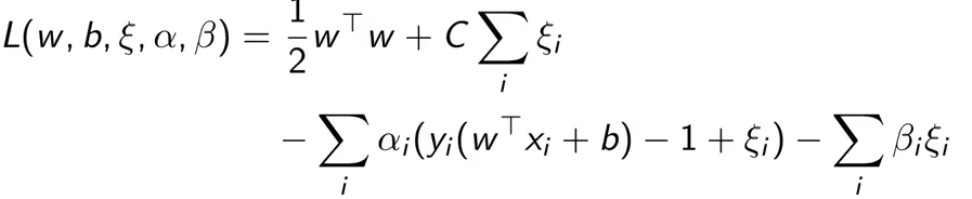
此时带约束的目标函数被重写成 min-max 问题。
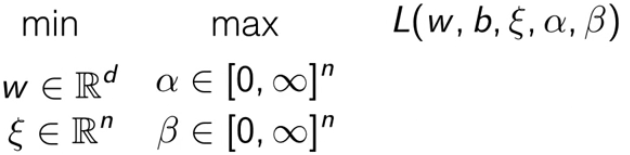
为了把原问题转化为对偶问题，需要转化为 max-min 问题。
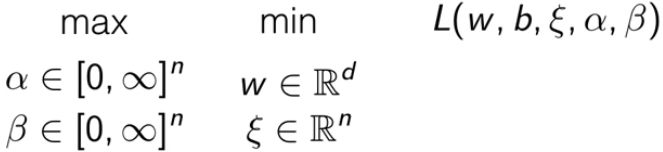
这样做不改变最后的解的原因是，这是一种强对偶关系。之后需要简化这个对偶问题。
KKT这位科学家指出了max-min问题中一定会成立的一些条件，这些被称为KKT条件：
① Stationarity。所有原变量和对偶变量的梯度为0。也就是无论最大化还是最小化的过程，都不能通过改变变量的值以得到比变量梯度为0时更好的得分。
② Primal feasibility。原问题中所有约束都要被满足。
③ Dual feasibility。要求对偶变量的约束要被满足（非负）。
④ Complementary Slackness。松弛互补。要么KKT乘子为0，要么不等式约束取等号（恰好满足）。
后面的分析会着重于①④。
然后回到拉格朗日函数，由于条件一，我们要对其中的变量进行求导，然后令他们梯度为0。
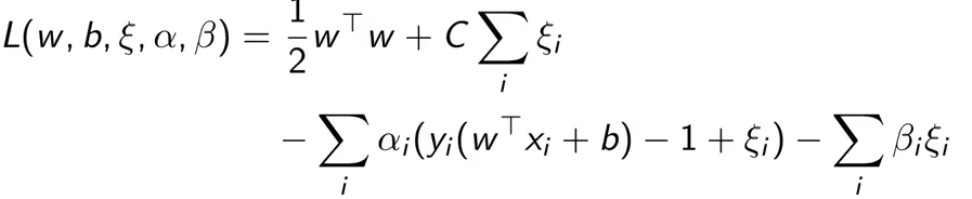
下图是各变量的梯度，以及梯度为0时的结论。
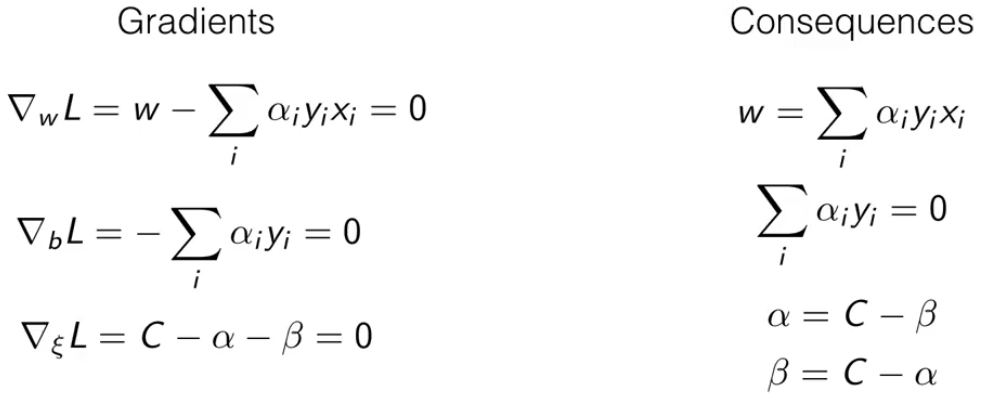
接下来使用这些结论推导后面的公式。
把拉格朗日里的乘积都拆开，然后把刚刚结论中的值一个一个带进去
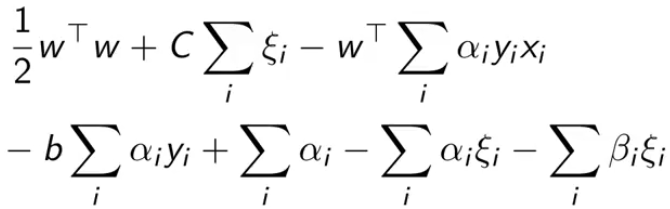
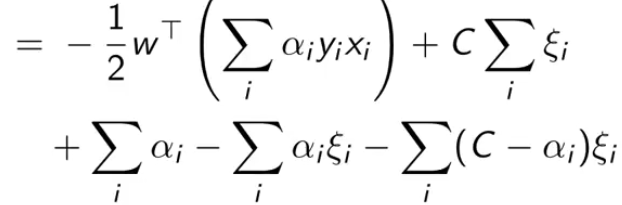
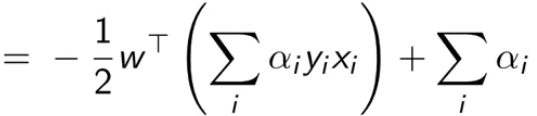
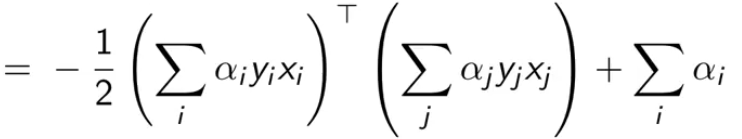
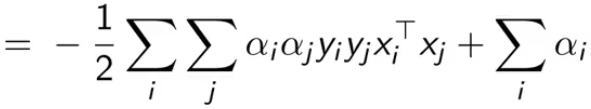
最终得到最后一个式子，我们是要最大化它（也就消除了原问题中的最小化项）
上式还有两个约束项，是由KKT条件推导的结论得到的。因为
，所以
；因为
而 β 非负，所以 α 小于 C。
下图是对偶SVM的最终形式：
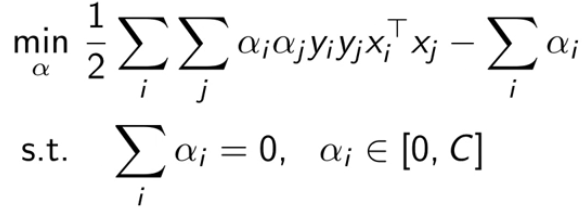
如果通过上式得到了 α，如何得到 w 和 b 。
前面推导得到了
而 b 要通过KKT条件的第4个条件来得到
其中 xi 是 αi ∈ [0, C] 之间的样本（通常使用多个样本均值估计b）。所以 b 如下。
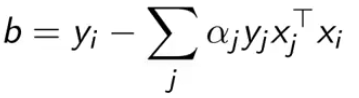
总结下，下图就是对偶SVM的所有内容。这就转化为一种简单的约束优化问题了。
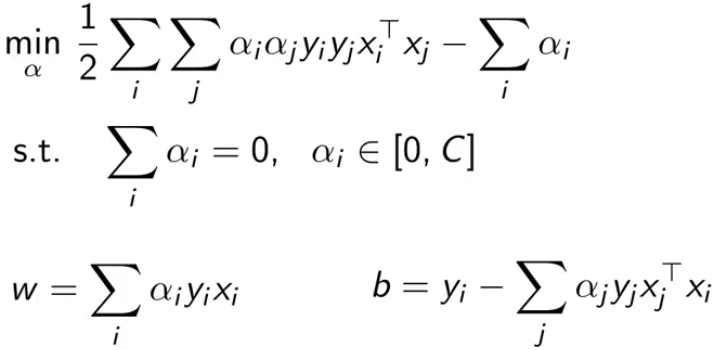
三、核函数
在对偶SVM中，我们可以观察到所有带有 x 的地方都有一定规律。它的优化不需考虑向量本身，只需要考虑两个数据向量的内积。
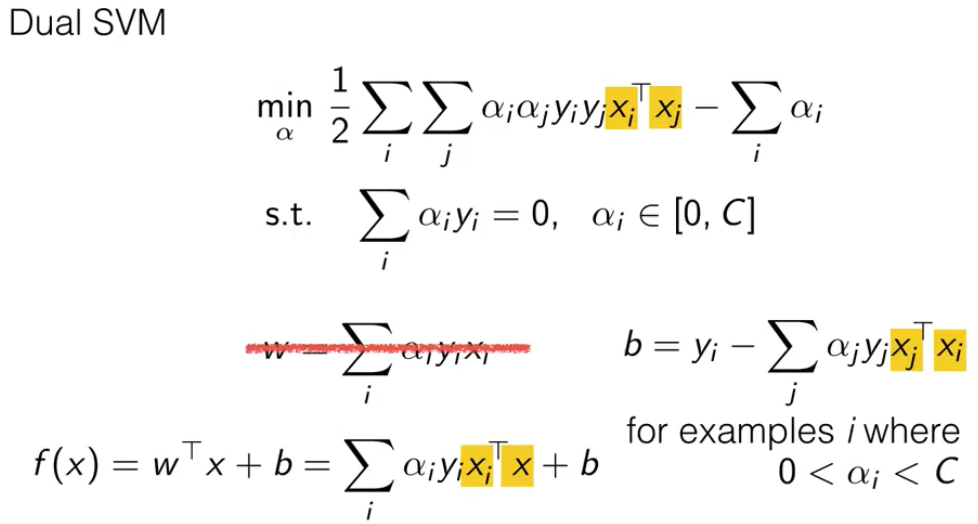
这使得对偶SVM在对非线性决策边界的数据进行学习时，可以使用一些技巧。就是将xiT xj 这个内积替换成核函数。
接下来说明什么是核函数。核函数是内积的一个一般化形式，也可以理解为空间的另一个内积。
核函数是做什么的。假设我们想分开下图红色和蓝色星星，用一条直线是肯定不行的。
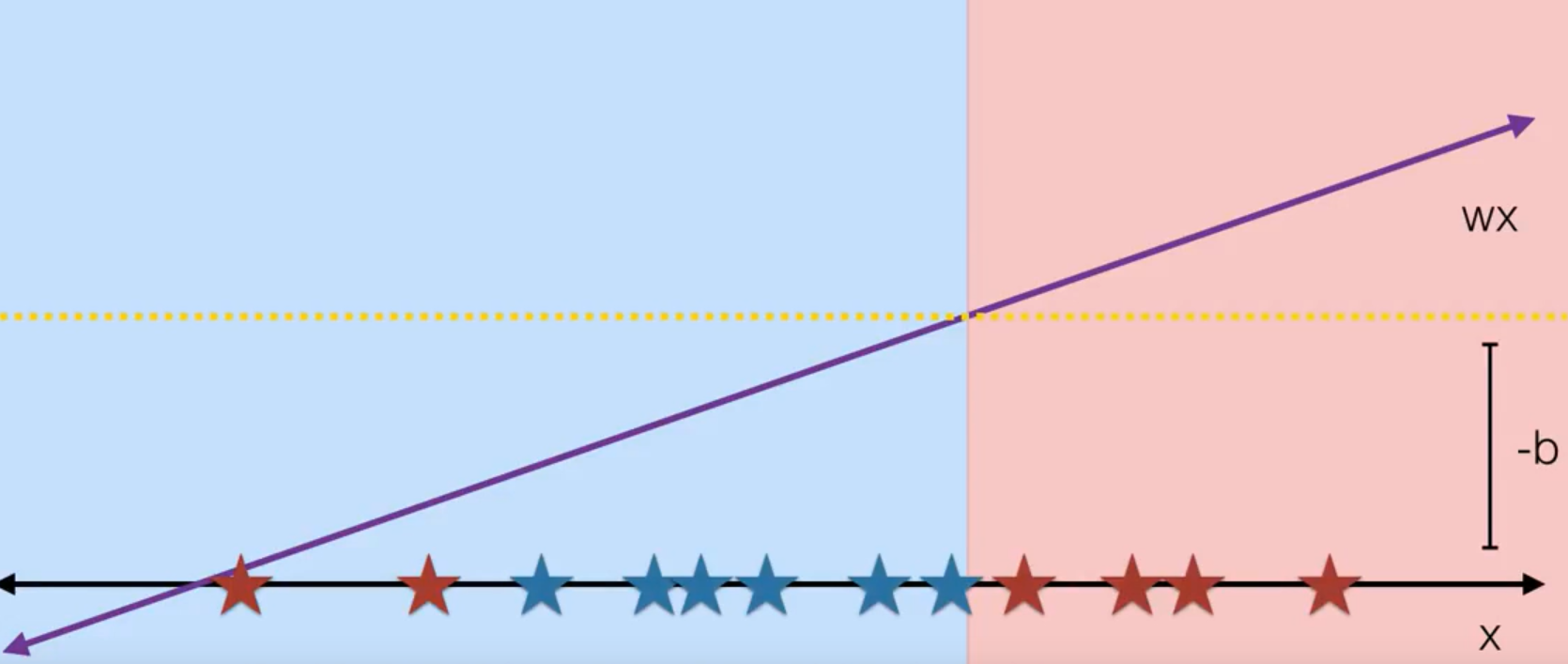
这时候考虑把 x 映射到另一个空间，把 x 映射为 x 的平方，这样决策边界就是抛物线形状。
这就是后面要说的多项式特征映射。把输入的维度（特征）组合相乘在一起，这样把原始的一阶输入扩展到更高阶。
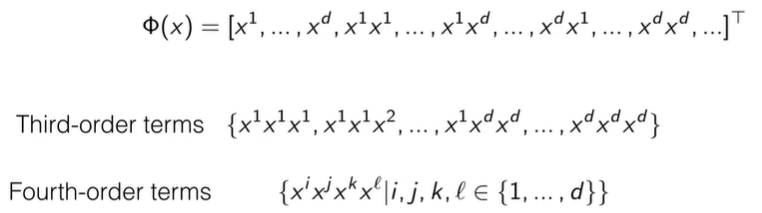
这样做会导致特征非常多，需要一些方法进行计算，就是核技巧。
对于核函数的内积，就是下图的每一项对应相乘，再加起来。
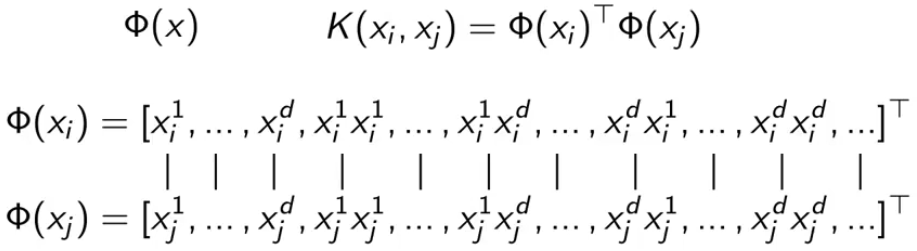
有一个技巧，就是把上图的乘积写成下面的形式，而不用展开每一项。（计算机中矩阵相乘比起计算数据向量快）
比如 M = 2 时，上式展开就是下面的。也就是二次多项式核。
RBF（径向基函数）
和高斯函数非常像。
那么已知上方的内积计算方式，它的特征映射是什么样？
对 exp 做泰勒展开：
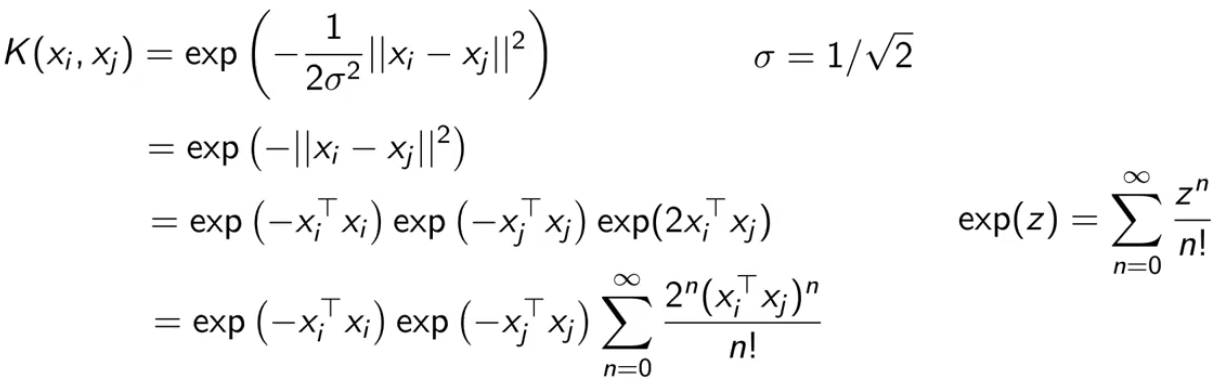
特征映射为：
综合常见的核函数来讲：
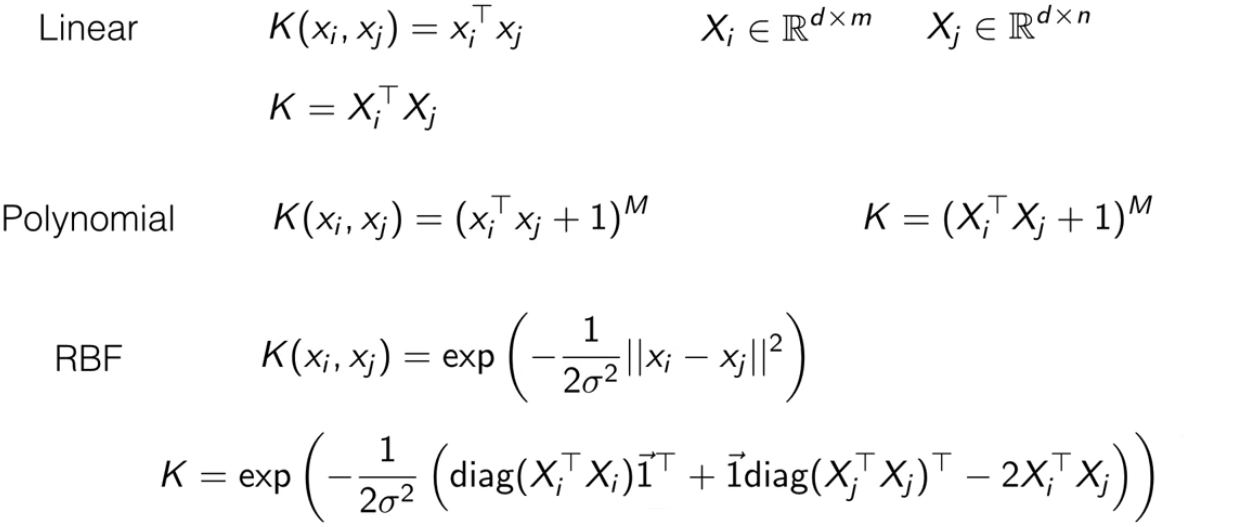
都可以计算出 gram 矩阵（所有(i, j)组合的核函数值组成的矩阵），就是图片里的每个核函数的第二个公式。这样计算量相对轻量。
只要一种算法使用了内积，都可以使用核函数代替，而没有实际计算向量的内积。
四、SVM的优化方法
主要有两个让SVM更快的解决方法：
1、SMO（序列最小优化）
2、梯度下降
都是启发于同样的思想，每次只考虑一个或两个样本
我们对原问题或对偶问题进行优化，都是在解一个二次规划问题。
前面说过 SVM 对偶问题不会出现 w 和 b，针对这个目标函数建立的优化方法就是SMO，使用的思想是一次只优化两个变量，而不是一次优化所有。专注于优化那些并非处在最优点的样本对应的变量值。
比如我们要优化 αa 和 αb，目标函数可拆成下式，其他常数与最小化无关就忽略了。
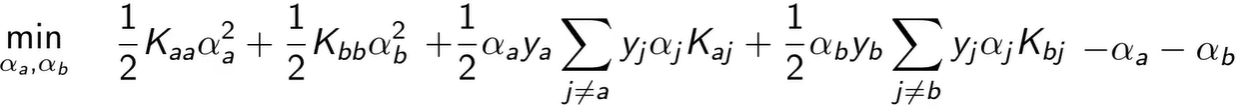
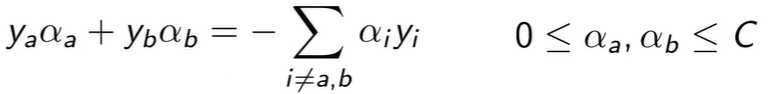
这个是二维的，它存在一个等式约束和一个不等式约束，求解会很快，而且它存在解析解（就是把 α 设为某个公式的值就好）。
所以 SMO 的主要思想是可以求解二维的最小化优化问题的解析解，可以遍历所有两个变量的组合或使用其他更好的办法，最后收敛到全局解。
下面是使用hinge loss进行梯度下降，这是从另一个角度看SVM原问题的目标函数。
之前使用了松弛变量，这里使用另一个完全等价的方式 hinge loss 来替代。
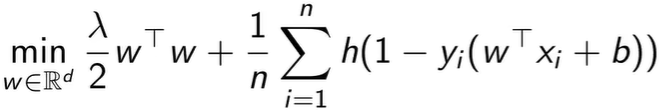
hinge 函数如果输入是负得到 0，输入是正就是原值。hinge 函数的输入是间隔约束被破坏的程度。除以 n 是用来缩放正则函数。
这种方法移除了松弛变量的约束，使之可以对目标函数求梯度
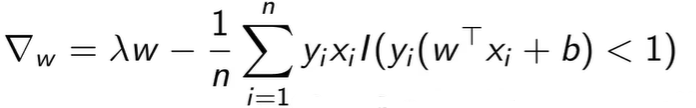
其中
这个函数表示样本是否分类错误，其值等于 0 或 1，如果正确就没有梯度，因为没有loss。
可以得到随机 SVM 的更新公式
