题目背景:
在这个(Canman)界的人都知道,世界上最伟大的修道者 —— (Felling),曾经结束了(Canman)的无垠盏之灾,守护了(Canman)的和平。在无垠盏之灾的最后,近神的(Felling)正在和堕入魔道的修道者,无垠灾的始作俑者(Neyii)进行最后的对峙。掌握着轮回之力的他,可以逆向流逝轮回,造成外爆内敛的奇点爆炸,比一般的爆炸要强悍数倍。
题目描述:
已知当前(Neyii)张开魔疆,把(Felling)包围了进去。(Felling)在魔疆中实力受到大幅的限制,甚至连时间和空间之力都被禁止了。但是魔疆是一把双面刃,包围了(Felling)的同时,(Neyii)也将自己的经络暴露在了(Felling)的面前。(Felling)知道这样下去自己终将陨落,所以打算孤注一掷,利用自己的轮回之力,引爆(Neyii)的经络!
已知当前(Neyii)的经络图由成百上千的穴位和经脉链接而成,经脉负责联通各个穴位。习武之人皆知,经脉内运气的流动是单向的,否则将会导致运气冲突,经脉爆裂的严重后果。如果引爆一个穴位,那么以这个穴位为起点的经脉都会报废。而如果一个穴位没有任何经脉流入供应,那么这个穴位就会进入闭脉状态,使(Felling)无法对其催动奇点爆炸。而(Felling)所引爆的穴位所蕴含的能量都将返还(Felling)。现在(Felling)所能释放奇点爆炸的次数已经不多了,他想在至多(K)次爆炸内,获得尽量多的能量。当然不一定要用完(K)次爆炸。题目不保证没有环, 但保证没有重边。保证权值不为负数,没有自环。
输入格式:
第一行,三个正整数(N, M, K)表示穴位数和经脉数和最多的爆炸次数。
第二行,(N)个整数(Data[i]),分别表示第(i)号穴位的能量。
下面(M)行,每行三个正整数,(X, Y)表示从(X)到(Y)有一条单向流动的经脉。
输出格式:
一行,一个整数,表示最多能获得的能量数。
输入样例 :
7 7 3
10 2 8 4 9 5 7
1 2
1 3
1 4
2 5
3 6
3 7
4 7
输出样例:
24
数据大小:
对于(10)%的数据,(1 leq N leq 10, 1 leq M leq 20)。
对于另外(30)%的数据,经络图无环。
对于另外(10)%的数据,有且只有一个点的入度为(0)。
对于(100)%的数据:(1 leq N leq 10000), (1 leq M leq 500003), (1 leq K leq 100003)
所有边权(leq 1000)
首先简化一下题面:
你现在有一张(N)个点(M)条边的一般有向图,你可以造成至多(K)次点上的爆炸,每次爆炸都可以获得这个点的点权。爆炸之后所有以这个点为起点的出边都会报废。如果一个点没有入边,那么不可以实施爆炸。请求最大化点权和。
首先我们考虑一张有向无环图。
你可以发现,假如你现在想要引爆(Now_1)和(Now_2),如果(Now_2)是从(Now_1)来的,那么我们一定是先引爆(Now_2),然后引爆(Now_1)获得的价值更大。
比如上图的(3和)(6)节点,如果我想要引爆这两个节点,那么我一定先引爆(6),因为如果我先引爆(3),那么会导致(6)不能被引爆。
而如果(Now_1)和(Now_2)是类似于一种“并列关系”的话,就不用彼此考虑。就比如(3)和(4)。
所以我们可以发现这个(DAG)上除了入度为(0)的那些点以外,其它的点我们都可以选。因为总有一种合法顺序可以让我们选完所有的点。因此(DAG)上我们只要删去所有入度为(0)的点,然后排序(For)到(K)即可。(30)分到手。
那么我们来考虑下图这种情况。
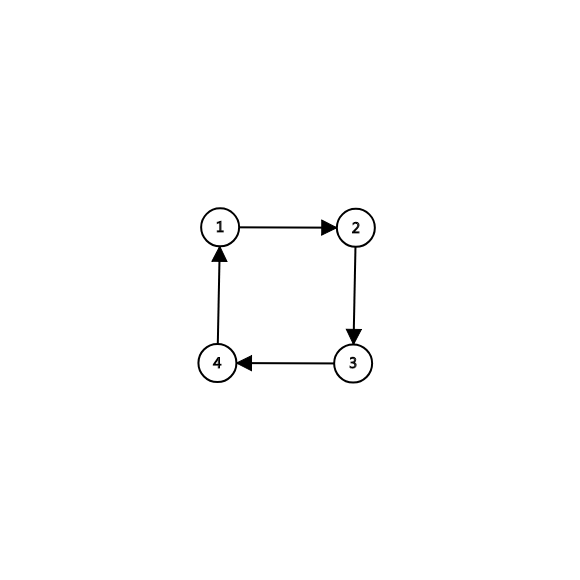
我们可以发现,如果我们从(4)开始引爆,那么(4)后引爆(3),(3)后引爆(2),(2)之后只剩了一个(1)没有引爆。当然换一个起点也是一样的。所以说,我们只需要舍弃一个点,那么其它的点都是可以被选中的。那么我们当然删去最小的点。
那么转而来看一般有向图。
我们发现这个情况下,原来的({1, 2, 3, 4})环都可以选了,因为多了一个入边({5 - > 1}),那么我们发现({1, 2, 3, 4})就可以看做是一个点。
那么得出算法:对于每一个强连通分量:
如果该强联通分量有入度,那么这个强联通分量里面的所有的点都可以选择。
如果该强联通分量没有入度,那么去掉一个点之后,其余的所有的点都可以选择。
所以算法流程如下:
- 缩点
- 对于每一条边,如果从(SCC_1)跑到了(SCC_2),那么认为(SCC_2)有入度,标记(Flag[SCC_2] = 1)
- (for)所有的(SCC_i),若(Flag[SCC_i] == 1)那么将该(SCC)里面的所有点加入数组。否则去掉里面点权最小的点,然后将其余的点加入数组。
- 对于上面说的那个数组,用(nth\_element)排序前(K)大,然后计算点权和。
算法实际上是一个比较奇妙的贪心。
标程:
#include <algorithm>
#include <iostream>
#include <algorithm>
#include <cstdlib>
#include <cstdio>
#include <cstring>
#include <vector>
#include <queue>
#include <cmath>
#include <map>
#define For1(i, A, B) for(register int i = (A), i##_end_ = (B); i <= i##_end_; ++ i)
#define For2(i, A, B) for(register int i = (A), i##_end_ = (B); i >= i##_end_; -- i)
#define MEM(Now, K) memset(Now, K, sizeof(Now))
#define CPY(Now, K) memcpy(Now, K, sizeof(Now))
#define Debug(Now) (cerr << Now << endl)
#define Min(A, B) (A < B ? A : B)
#define Max(A, B) (A < B ? B : A)
#define SCPY(A, B) strcpy(A, B)
#define Inf 0x7fffffff
#define RE register
#define IL inline
#define MAXN 100010
#define MAXM 500010
#define _X first
#define _Y second
using namespace std ;
typedef unsigned long long ULL ;
typedef pair<long long, int> PLI;
typedef pair<int, int> PII;
typedef unsigned int UINT;
typedef long double LDB;
typedef long long LL ;
typedef double DB ;
IL int Read(){
LL X = 0, F = 1 ; char ch = getchar() ;
while(ch < '0' || ch > '9'){ if(ch == '-') F = - 1 ; ch = getchar() ; }
while(ch <= '9' && ch >= '0') X = (X << 1) + (X << 3) + (ch ^ 48), ch = getchar() ;
return X * F ;
}
IL double DBRead(){
double X = 0, Y = 1.0 ; LL W = 0 ; char ch = 0 ;
while(! isdigit(ch)) { W |= ch == '-' ; ch = getchar() ; }
while(isdigit(ch)) X = X * 10 + (ch ^ 48), ch = getchar() ;
ch = getchar();
while(isdigit(ch)) X += (Y /= 10) * (ch ^ 48), ch = getchar() ;
return W ? - X : X ;
}
IL void Print(/*LL*/ LL X){
if(X < 0) putchar('-'), X = - X ;
if(X > 9) Print(X / 10) ; putchar(X % 10 + '0') ;
//cout << endl ;
//cout << " " ;
}
//----------------------------------以上是精致小巧的缺省源......
LL N, M, K, Data[MAXN], Ans ;
struct Node{
LL From, To, Next ;
}Edge[MAXM] ;
LL Head[MAXN], Total ;
void Add(LL F, LL T){
Total ++ ;
Edge[Total].From = F ;
Edge[Total].To = T ;
Edge[Total].Next = Head[F] ;
Head[F] = Total ;
}
LL Dfn[MAXN], Low[MAXN], Deep, Cnt, Flag[MAXN] ;
LL Stack[MAXN], Insta[MAXN], Top ;
LL Belong[MAXN], Est[MAXN], MIN[MAXN] ;
LL Finally[MAXN], All ;
//Finally表示最终的答案数组
//All表示“预选”答案一共有多少个。
void Tarjan(LL Now){ //缩点自然不用说
Dfn[Now] = Low[Now] = ++ Deep ;
Stack[++ Top] = Now ; Insta[Now] = 1 ;
for(LL i = Head[Now]; i; i = Edge[i].Next){
if(! Dfn[Edge[i].To]){
Tarjan(Edge[i].To) ;
Low[Now] = min(Low[Now], Low[Edge[i].To]) ;
} else if(Insta[Edge[i].To])
Low[Now] = min(Low[Now], Dfn[Edge[i].To]) ;
}
if(Low[Now] == Dfn[Now]){
Cnt ++ ; LL Pass ;
do{
Pass = Stack[Top --] ;
if(Est[Cnt] > Data[Pass])
MIN[Cnt] = Pass, Est[Cnt] = Data[Pass] ;
//MIN[]和EST[]求的是每一个SCC里面最小的点
//其中MIN[]是表示点,EST[]表示点权
Belong[Pass] = Cnt ;
Insta[Pass] = 0 ;
}while(Now != Pass) ;
}
}
bool CMP(LL X, LL Y){
return X > Y ;
}
int main() {
N = Read(), M = Read(), K = Read() ;
memset(Est, 127, sizeof(Est)) ;
for(LL i = 1; i <= N; i ++)
Data[i] = Read() ;
for(LL i = 1; i <= M; i ++){
LL F = Read(), T = Read() ;
Add(F, T) ;
}
for(LL i = 1; i <= N; i ++)
if(! Dfn[i]) Tarjan(i) ;// 缩点
//下面这一行是一个判断。如果存在一条边使得这条边从SCC1到SCC2
//那么SCC2就属于我们说的又入度的强联通分量。
for(LL i = 1; i <= M; i ++){
if(Belong[Edge[i].From] != Belong[Edge[i].To])
Flag[Belong[Edge[i].To]] = 1 ;
//Flag[]记录这个SCC有没有入度。
}
for(LL i = 1; i <= Cnt; i ++)
if(! Flag[i])
Data[MIN[i]] = - 1 ;
for(LL i = 1; i <= N; i ++){
if(Data[i] == -1) continue ;
Finally[++ All] = - Data[i] ;
}
nth_element(Finally + 1, Finally + K + 1, Finally + All + 1) ;
/*由于我们只需要知道前K个数而并不需要知道具体顺序,所以可以直接使用
STL里面的nth_element而不用sort*/
for(LL i = 1; i <= K; i ++)
Ans += - Finally[i] ;
//点权是存的相反数,好用nth_element
printf("%lld", Ans) ;
return 0 ;
}