“tarjan陪伴强联通分量
生成树完成后思路才闪光
欧拉跑过的七桥古塘
让你 心驰神往”----《膜你抄》
自从听完这首歌,我就对tarjan开始心驰神往了,不过由于之前水平不足,一直没有时间学习。这两天好不容易学会了,写篇博客,也算记录一下。
一、tarjan求强连通分量
1、什么是强连通分量?
引用来自度娘的一句话:
“有向图强连通分量:在有向图G中,如果两个顶点vi,vj间(vi>vj)有一条从vi到vj的有向路径,同时还有一条从vj到vi的有向路径,则称两个顶点强连通(strongly connected)。如果有向图G的每两个顶点都强连通,称G是一个强连通图。有向图的极大强连通子图,称为强连通分量(strongly connected components)。”
一脸懵逼......不过倒也不难理解。
反正就是在图中找到一个最大的图,使这个图中每个两点都能够互相到达。这个最大的图称为强连通分量,同时一个点也属于强连通分量。
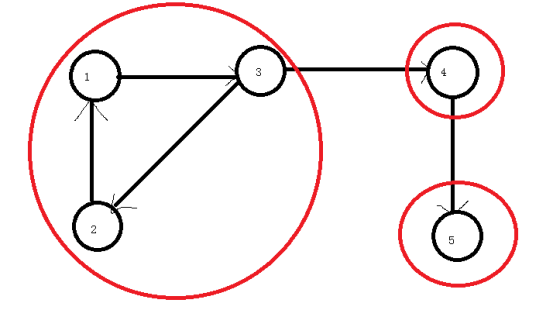
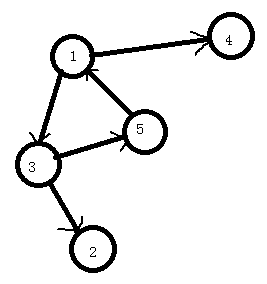
如图中强连通分量有三个:1-2-3,4,5
2、强连通分量怎么找?
噫......当然,通过肉眼可以很直观地看出1-2-3是一组强连通分量,但很遗憾,机器并没有眼睛,所以该怎么判断强连通分量呢?
如果仍是上面那张图,我们对它进行dfs遍历。
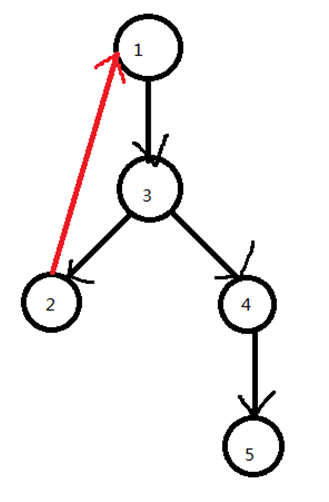
可以注意到红边非常特别,因为如果按照遍历时间来分类的话,其他边都指向在自己之后被遍历到的点,而红边指向的则是比自己先被遍历到的点。
如果存在这么一条边,那么我们可以yy一下,emmmm.......
从一个点出发,一直向下遍历,然后忽得找到一个点,那个点竟然有条指回这一个点的边!
那么想必这个点能够从自身出发再回到自身
想必这个点和其他向下遍历的该路径上的所有点构成了一个环,
想必这个环上的所有点都是强联通的。
但只是强联通啊,我们需要求的可是强连通分量啊......
那怎么办呢?
我们还是yy出那棵dfs树
不妨想一下,什么时候一个点和他的所有子孙节点中的一部分构成强连通分量?
他的子孙再也没有指向他的祖先的边,却有指向他自己的边
因为只要他的子孙节点有指向祖先的边,显然可以构成一个更大的强联通图。
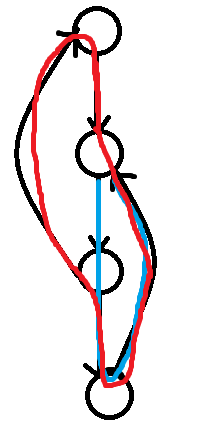
比如说图中红色为强连通分量,而蓝色只是强联通图
那么我们只需要知道这个点u下面的所有子节点有没有连着这个点的祖先就行了。
但似乎还有一个问题啊......
我们怎么知道这个点u它下面的所有子节点一定是都与他强联通的呢?
这似乎是不对的,这个点u之下的所有点不一定都强联通
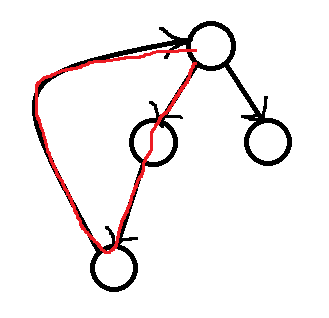
那么怎么在退回到这个点的时候,知道所有和这个点u构成强连通分量的点呢?
开个栈记录就行了
什么?!这么简单?
没错~就是这么简单~
如果在这个点之后被遍历到的点已经能与其下面的一部分点(也可能就只有他一个点)已经构成强连通分量,即它已经是最大的。
那么把它们一起从栈里弹出来就行了。
所以最后处理到点u时如果u的子孙没有指向其祖先的边,那么它之后的点肯定都已经处理好了,一个常见的思想,可以理解一下。
所以就可以保证栈里留下来u后的点都是能与它构成强连通分量的。
似乎做法已经明了了,用程序应该怎么实现呢?
所以为了实现上面的操作,我们需要一些辅助数组
(1)、dfn[ ],表示这个点在dfs时是第几个被搜到的。
(2)、low[ ],表示这个点以及其子孙节点连的所有点中dfn最小的值
(3)、stack[ ],表示当前所有可能能构成是强连通分量的点。
(4)、vis[ ],表示一个点是否在stack[ ]数组中。
那么按照之上的思路,我们来考虑这几个数组的用处以及tarjan的过程。
假设现在开始遍历点u:
(1)、首先初始化dfn[u]=low[u]=第几个被dfs到
dfn可以理解,但为什么low也要这么做呢?
因为low的定义如上,也就是说如果没有子孙与u的祖先相连的话,dfn[u]一定是它和它的所有子孙中dfn最小的(因为它的所有子孙一定比他后搜到)。
(2)、将u存入stack[ ]中,并将vis[u]设为true
stack[ ]有什么用?
如果u在stack中,u之后的所有点在u被回溯到时u和栈中所有在它之后的点都构成强连通分量。
(3)、遍历u的每一个能到的点,如果这个点dfn[ ]为0,即仍未访问过,那么就对点v进行dfs,然后low[u]=min{low[u],low[v]}
low[ ]有什么用?
应该能看出来吧,就是记录一个点它最大能连通到哪个祖先节点(当然包括自己)
如果遍历到的这个点已经被遍历到了,那么看它当前有没有在stack[ ]里,如果有那么low[u]=min{low[u],low[v]}
如果已经被弹掉了,说明无论如何这个点也不能与u构成强连通分量,因为它不能到达u
如果还在栈里,说明这个点肯定能到达u,同样u能到达他,他俩强联通。
(4)、假设我们已经dfs完了u的所有的子树那么之后无论我们再怎么dfs,u点的low值已经不会再变了。
那么如果dfn[u]=low[u]这说明了什么呢?
再结合一下dfn和low的定义来看看吧
dfn表示u点被dfs到的时间,low表示u和u所有的子树所能到达的点中dfn最小的。
这说明了u点及u点之下的所有子节点没有边是指向u的祖先的了,即我们之前说的u点与它的子孙节点构成了一个最大的强连通图即强连通分量
此时我们得到了一个强连通分量,把所有的u点以后压入栈中的点和u点一并弹出,将它们的vis[ ]置为false,如有需要也可以给它们打上相同标记(同一个数字)
tarjan到此结束
至于手模?tan90°!网上有不少大佬已经手摸了不少样例了,想必不需要本蒟蒻再补充了。
结合上面四步代码已经可以写出了:

对了,tarjan一遍不能搜完所有的点,因为存在孤立点或者其他
所以我们要对一趟跑下来还没有被访问到的点继续跑tarjan
怎么知道这个点有没有被访问呢?
看看它的dfn是否为0!

这看起来似乎是o(n^2)的复杂度,但其实均摊下来每个点只会被遍历一遍
所以tarjan的复杂度为o(n)。
来一道例题吧,这是模板题,应该做到提交框AC
[USACO06JAN]牛的舞会The Cow Prom
给你n个点,m条边,求图中所有大小大于1的强连通分量的个数
5 4
2 4
3 5
1 2
4 1
1
显然是tarjan水题,数出强连通分量的个数,给每个强连通分量的点染色,统计出每个强连通分量中点的个数,如果大于一,则答案加一。
代码:
#include<queue> #include<cstdio> #include<vector> #include<cstring> #include<iostream> #include<algorithm> using namespace std; #define inf 0x3f3f3f3f vector<int> g[10010]; int color[10010],dfn[20020],low[20020],stack[20020],vis[10010],cnt[10010]; int deep,top,n,m,sum,ans; void tarjan(int u) { dfn[u]=++deep; low[u]=deep; vis[u]=1; stack[++top]=u; int sz=g[u].size(); for(int i=0;i<sz;i++) { int v=g[u][i]; if(!dfn[v]) { tarjan(v); low[u]=min(low[u],low[v]); } else { if(vis[v]) { low[u]=min(low[u],low[v]); } } } if(dfn[u]==low[u]) { color[u]=++sum; vis[u]=0; while(stack[top]!=u) { color[stack[top]]=sum; vis[stack[top--]]=0; } top--; } } int main() { scanf("%d%d",&n,&m); for(int i=1;i<=m;i++) { int from,to; scanf("%d%d",&from,&to); g[from].push_back(to); } for(int i=1;i<=n;i++) { if(!dfn[i]) { tarjan(i); } } for(int i=1;i<=n;i++) { cnt[color[i]]++; } for(int i=1;i<=sum;i++) { if(cnt[i]>1) { ans++; } } printf("%d ",ans); }
二、tarjan缩点
其实这也是利用了tarjan求强连通分量的方法,对于一些贡献具有传导性,比如友情啊、路径上的权值啊等等。
思想就是因为强连通分量中的每两个点都是强连通的,可以将一个强连通分量当做一个超级点,而点权按题意来定。
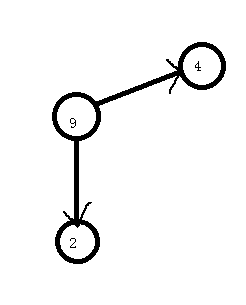
来看一道题吧。
poj2186 Popular Cows
告诉你有n头牛,m个崇拜关系,并且崇拜具有传递性,如果a崇拜b,b崇拜c,则a崇拜c,求最后有几头牛被所有牛崇拜。
Sample Input
3 3
1 2
2 1
2 3
Sample Output
1
显然一个强联通分量内的所有点都是满足条件的,我们可以对整张图进行缩点,然后就简单了。
剩下的所有点都不是强连通的,现在整张图就是一个DAG(有向无环图)
那么就变成一道水题了,因为这是一个有向无环图,不存在所有点的出度都不为零的情况。
所以必然有1个及以上的点出度为零,如果有两个点出度为零,那么这两个点肯定是不相连的,即这两圈牛不是互相崇拜的,于是此时答案为零,如果有1个点出度为0,那么这个点就是被全体牛崇拜的,
这个点可能是一个强联通分量缩成的超级点,所以应该输出整个强联通分量中点的个数。
代码:
#include<cmath> #include<cstdio> #include<vector> #include<cstring> #include<iostream> #include<algorithm> using namespace std; int dfn[10010],low[10010],vis[10010],stack[10010],color[10010],du[10010],cnt[10010]; int n,m,top,sum,deep,tmp,ans; vector<int> g[10010]; void tarjan(int u) { dfn[u]=low[u]=++deep; vis[u]=1; stack[++top]=u; int sz=g[u].size(); for(int i=0; i<sz; i++) { int v=g[u][i]; if(!dfn[v]) { tarjan(v); low[u]=min(low[u],low[v]); } else { if(vis[v]) { low[u]=min(low[u],low[v]); } } } if(dfn[u]==low[u]) { color[u]=++sum; vis[u]=0; while(stack[top]!=u) { color[stack[top]]=sum; vis[stack[top--]]=0; } top--; } } int main() { while(scanf("%d%d",&n,&m)!=EOF) { memset(vis,0,sizeof(du)); memset(vis,0,sizeof(low)); memset(dfn,0,sizeof(dfn)); memset(vis,0,sizeof(vis)); memset(vis,0,sizeof(cnt)); memset(vis,0,sizeof(color)); memset(vis,0,sizeof(stack)); for(int i=1; i<=n; i++) { g[i].clear(); } for(int i=1; i<=m; i++) { int from,to; scanf("%d%d",&from,&to); g[from].push_back(to); } for(int i=1; i<=n; i++) { if(!dfn[i]) { tarjan(i); } } for(int i=1; i<=n; i++) { int sz=g[i].size(); for(int j=0; j<sz; j++) { int v=g[i][j]; if(color[v]!=color[i]) { du[color[i]]++; } } cnt[color[i]]++; } for(int i=1; i<=sum; i++) { if(du[i]==0) { tmp++; ans=cnt[i]; } } if(tmp==0) { printf("0 "); } else { if(tmp>1) { printf("0 "); } else { printf("%d ",ans); } } } }
三、tarjan求割点、桥
1、什么是割点、桥
再来引用一遍度娘:
在一个无向图中,如果有一个顶点集合,删除这个顶点集合以及这个集合中所有顶点相关联的边以后,图的连通分量增多,就称这个点集为割点集合。
又是一脸懵逼。。。。
总而言之,就是这个点维持着双联通的继续,去掉这个点,这个连通分量就无法在维持下去,分成好几个连通分量。
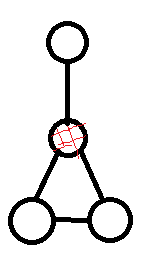
比如说上图红色的即为一个割点。
桥:
如果一个无向连通图的边连通度大于1,则称该图是边双连通的 (edge biconnected),简 称双连通或重连通。一个图有桥,当且仅当这个图的边连通度为 1,则割边集合的唯一元素 被称为桥(bridge),又叫关节边(articulationedge)。一个图可能有多个桥。(该资料同样来自百度)
对于连通图有两种双联通,边双和点双,桥之于边双如同割点之于点双

如图则是一个桥。
2、割点和桥怎么求?
与之前强连通分量中的tarjan差不多。但要加一个特判,根节点如果有两个及以上的儿子,那么他也是割点。

模板题:洛谷3388
求割点的个数和数量
代码:
#include<cstdio> #include<vector> #include<cstring> #include<iostream> #include<algorithm> #define hi printf("hi!"); using namespace std; vector<int> g[10010]; int dfn[10010],low[10010],iscut[10010],son[10010]; int deep,root,n,m,ans; int tarjan(int u,int fa) { int child=0,lowu; lowu=dfn[u]=++deep; int sz=g[u].size(); for(int i=0;i<sz;i++) { int v=g[u][i]; if(!dfn[v]) { child++; int lowv=tarjan(v,u); lowu=min(lowu,lowv); if(lowv>dfn[u]) { iscut[u]=1; } } else { if(v!=fa&&dfn[v]<dfn[u]) { lowu=min(lowu,dfn[v]); } } } if(fa<0&&child==1) { iscut[u]=false; } low[u]=lowu; return lowu; } int main() { scanf("%d%d",&n,&m); for(int i=1;i<=m;i++) { int from,to; scanf("%d%d",&from,&to); g[from].push_back(to); g[to].push_back(from); } for(int i=1;i<=n;i++) { if(!dfn[i]) { root=i; tarjan(i,-1); } } for(int i=1;i<=n;i++) { if(iscut[i]) { ans++; } } printf("%d ",ans); for(int i=1;i<=n;i++) { if(iscut[i]) { printf("%d ",i); } } }
桥的求法也差不多
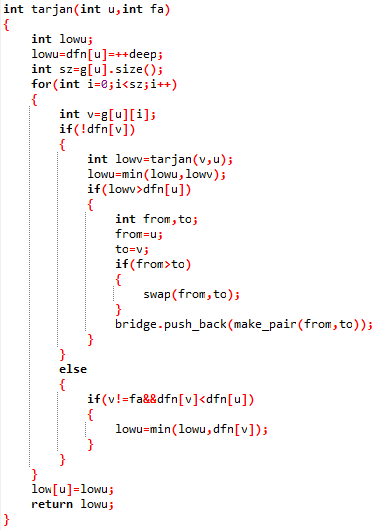
并没有找到模板题目,所以只好把没检验过的代码放着了......如有错误还请留言指正
#include<cstdio> #include<vector> #include<cstring> #include<iostream> #include<algorithm> #define hi printf("hi!"); using namespace std; vector<pair<int,int> >bridge; vector<int> g[10010]; int dfn[10010],low[10010]; int deep,root,n,m,ans; int tarjan(int u,int fa) { int lowu; lowu=dfn[u]=++deep; int sz=g[u].size(); for(int i=0;i<sz;i++) { int v=g[u][i]; if(!dfn[v]) { int lowv=tarjan(v,u); lowu=min(lowu,lowv); if(lowv>dfn[u]) { int from,to; from=u; to=v; if(from>to) { swap(from,to); } bridge.push_back(make_pair(from,to)); } } else { if(v!=fa&&dfn[v]<dfn[u]) { lowu=min(lowu,dfn[v]); } } } low[u]=lowu; return lowu; } int main() { scanf("%d%d",&n,&m); for(int i=1;i<=m;i++) { int from,to; scanf("%d%d",&from,&to); g[from].push_back(to); g[to].push_back(from); } for(int i=1;i<=n;i++) { if(!dfn[i]) { root=i; tarjan(i,-1); } } for(int i=0;i<bridge.size();i++) { printf("%d %d ",bridge[i].first,bridge[i].second); } }
おわり