从一道动态规划到卡特兰数
LeetCode 96
题目链接:https://leetcode-cn.com/problems/unique-binary-search-trees/
题意:给定一个整数 n,求以 1 ... n 为节点组成的二叉搜索树有多少种?
n = 3 时:

动态规划
思路:从 1 开始到 n ,每次以这个数为根,左子树存放比它小的数,右子树存放比它大的数。每个根不重复,因此每个树也必定不重复。
左子树和右子树,又可以按照这个规则去生成新的树。

例如:n = 3的时候
1为根: 比 1 小的数只有 0,不用管。比 1 大的数有 2 和 3。
拿 2 和 3 来生成一棵树和拿 1 和 2 来生成一棵树的种数是不是相同的?那么 1 和 2 能生成多少种树呢?
2为根: 比 2 小的是 1,比 2 大的是 3。这里只有 1 种。
3为根: 比 3 小的是 1 和 2,1 和 2 能生成多少种树呢?
我们先暂停思维,来到一个新的问题。 n = 2 的时候,结果应该是多少?

n = 2 的时候,按照我们之前的方法。
1 为根:比 1 大的数只有 2, 这里有 1 种。
2 为根:比 2 小的数只有 1, 这里有 1 种。
那答案就应该是 2 种。
解决了 n = 2 的问题,那 n = 3 的问题就也解决了。 ans = 2 + 1 + 2 = 5。
我们来看一般情况。输入一个 n 。
定义一个 F(i) 表示以 i 为根,生成的树的种数。
定义一个 G(n) 表示输入 n 的时候,输出的结果。此处一定要注意 F 与 G 的区别。
以 i 为根的时候,能生成多少种树?
比 i 小的有 i - 1 个,比 i 大的有 n - i 个。因此左子树有 i - 1 个, 右子树有 n - i 个数。那么,F(i) = G(i - 1) * G(n - i)。
而我们求的 G(n) = F(1) + F(2) + …… + F(n)。
把两个公式综合 :
G(n) = $displaystyle sum^{n}_{i = 1}{G(i-1)}*G(n-i)$
d[0] = 1; // 0 的时候特殊处理
for (int i = 1; i <= n; i++)
for (int j = 1; j <= i; j++)
d[i] += d[j-1] * d[i-j];
以上是利用动态规划求解的思路。
时间复杂度:O(n^2)
空间复杂度:O(n)
Catalan公式
这个题目还有一种很强的解法,卡特兰公式。卡特兰公式和排列组合有很大关系,不属于偏难怪解法,有很多算法和数据结构的问题本质上就是卡特兰公式的应用。比如二叉树的形态数,出栈序列数,括号匹配问题等。公式不要紧,没必要去硬背。主要是理解卡特兰问题应用的特征,把问题抽象到已有模型中来。
Catalan 递推项满足:
C(n) = C(0) * C(n-1) + C(1) * C(n-2) + … + C(n-2) * C(1) + C(n-1) * C(0)
Catalan 通项公式:$C_{n} = $ $ {1} over {n+1}$ $C_{2n}^{n}$
Catalan 递推公式1:$C_{n+1} = $ $ {4n + 2} over {n + 2}$ $C_{n}$
Catalan 性质:$C_{n} = $ $C_{2n}^{n}$ - $ C_{2n}^{n-1}$
这个题目里面,由我们上面的 G(n) 很容易可以看出是一个卡特兰的应用。
我们用它的递推公式来求解。
求$C_{n}$的值,$C_{n} = $ $ {4n + 2} over {n + 2}$ $C_{n-1}$。公式顺推即可得到答案。类比斐波那契最简解法。
long ans = 1;
for(int i = 0; i < n; i++)
ans = ans * 2 * (2 * i + 1) / (i + 2);
return (int) ans;
时间复杂度: O(n)
空间复杂度: O(1)
Catalan应用
例题1:括号序列
给 n 对括号,可以合成的合法序列有多少种?

-
首先计算一共的序列种数。n 对括号, 一共有 2n 个位置。我们选出其中 n 个位置放放置左括号,剩下的位置肯定就是右括号了。因此一共的种数为: $C_{2n} ^ {n} $ 。
-
接下来找出非法的括号序列数。每个非法的序列,在它的奇数位置,一定存在右括号数量大于左括号的数量。
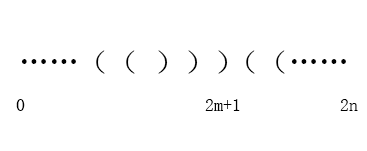
在上图中:第 2m + 1 的时候,右括号大于左括号,因此该序列非法。
在 2m + 1 前:
右括号数量为: m + 1
左括号数量为: m
在 2m + 1后:
总的数量: n - 2m - 1
左括号有: n - 2m - 1 - (m + 1) = n - m
右括号有: n - 2m - 1 - m = n - m - 1
这个时候我们将右边的左括号和右括号位置置换(总的组合数量不会受到影响)。那么在整个序列 2n 个位置中:
右括号的数量为: m + 1 + n - m = n + 1
左括号的数量为: m + n - m - 1 = n - 1
在长度为 2n 里面有 n + 1 个右括号,数量为:$ C_{2n} ^ { n+1} $ 。你也可以理解从左括号的角度去看:$C_{2n} ^ {n-1} $ 。
在上面两个步骤以后,我们得到的合法序列数:$C_{2n} ^ {n} $ - $C_{2n} ^ {n-1} $ 。这就是 Catalan 公式的性质公式。知道是 Catalan,我们就可以用刚刚的方法求解问题的答案。
例题2 :一个栈(无穷大)的进栈序列为1,2,3,…,n,有多少个不同的出栈序列?
例题3 :给出一个n,要求一个长度为2n的01序列,使得序列的任意前缀中1的个数不少于0的个数, 有多少个不同的01序列?
例题4 :2n个人要买票价为五元的电影票,每人只买一张,但是售票员没有钱找零。其中,n个人持有五元,另外n个人持有十元,问在不发生找零困难的情况下,有多少种排队方法?(阿里有个笔试题根据这个变化的)