本节主要说明当前主流的VIO算法流程。课程来源于B站。
高斯牛顿法
误差项:
$$
e(x+Delta x)=e(x)+J(x)Delta x
$$
- 一次观测
- 多次观测
- 逆深度 + VIO
EKF滤波和优化
- EKF铝箔相当于之迭代一次的优化,区别是滤波仅考虑上一帧的影响,而优化则考虑所有帧的影响
- 多次优化精度比滤波高,但效率低于滤波,因优化可以迭代多次,不断优化线性化点,是误差最小
IMU预积分
- 积分下一个时刻的PVQ作为视觉初始值
- 预计分相邻帧的PVQ变化量,作为IMU的约束
- 计算IMU误差的协方差和jacobian

VIO分类
将视觉约束就加到联合优化是紧耦合
将视觉约束后的位姿加入到联合优化是松耦合

MSCKF
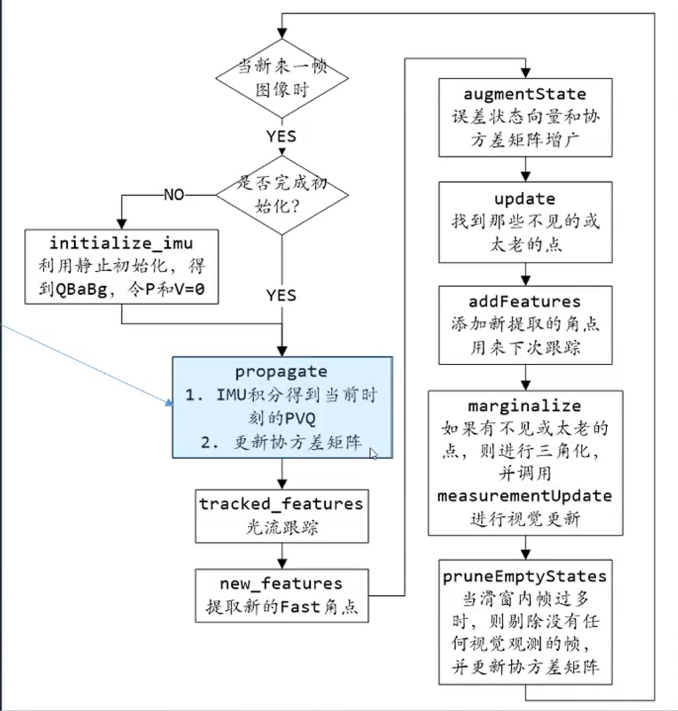
具体流程如下所示:
- 初始化
- IMU预测
- 视觉跟踪
- 视觉增广
- 视觉更新—选老点或者看不见的点
- 视觉更新—边缘化
- 剔除老帧
误差状态向量
$$
hat{X_k}^{(15+6N) imes1} = [hat{X_{IMU_k}} delta heta_{C_1} ce{G}hat{p}{C_1} …ce{^{G}hat{p}{c_N} ce{G}hat{p}_{C_N}}]
$$
$$
hat{X}_{IMU}_k^{15 imes1}=[delta heta_I hat{b_g}spacece{G}hat{v}_Ihat{b}_aspace ce{G}hat{p}_I ]^T
$$
每得到一个新图像以后需要对协方差矩阵做一个增广

成熟的路标点 表示窗口内各帧都看得到的点
因子图
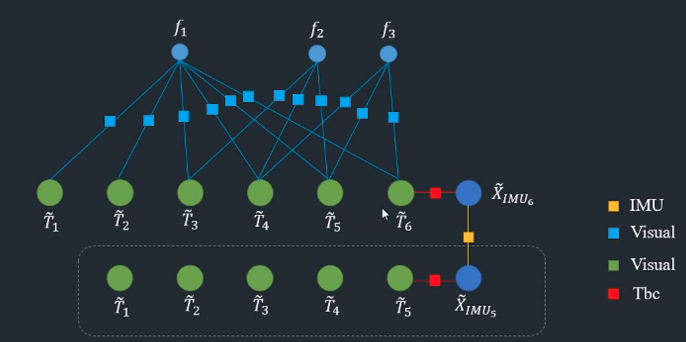
Tbc表示IMU与相机间的转换矩阵
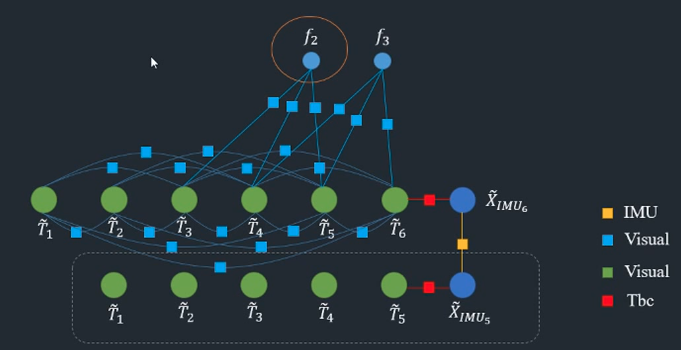
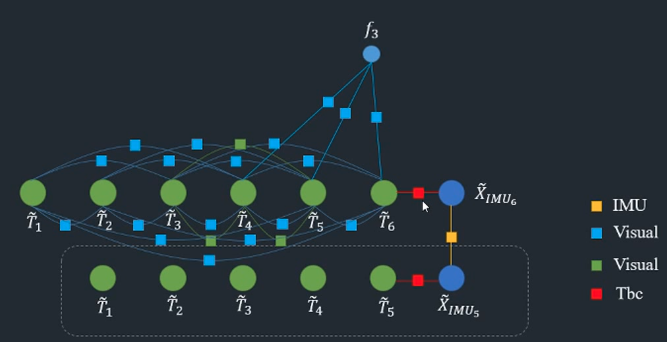
路标点边缘化完后就可以了
第j个路标点的所有视觉误差为
$$
r^{2M imes1}cong H_x^{2M imes(15+6N) ilde{X}^{(15+N) imes1}}+H_f^{2M imes3}ce{G}hat{p}_{f_j}^{3 imes1}+n^{2M imes1}
$$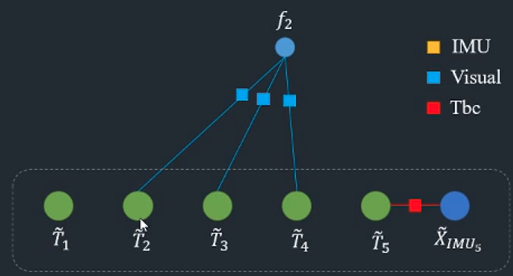
将r投影到Hf的左零空间,想党羽对路标点进行边缘化,将边缘化约束来优化共视帧。
$$
r_0^(2M-3M_L) imes1=A^Tr^2M imes1cong A^TH_{x}^{2M imes(15+6N)} ilde{X}^{(15+6N) imes1}+A^Tn^(2M imes1)
$$
ROVIO
复杂 不常用
流程
- IMU预测
- 视觉更新
- IEKF
- 相机模型
- 像素坐标校正
- 光度误差
- QR分解
- Paych提取及Warp计算
- 路标点质量评价及维护
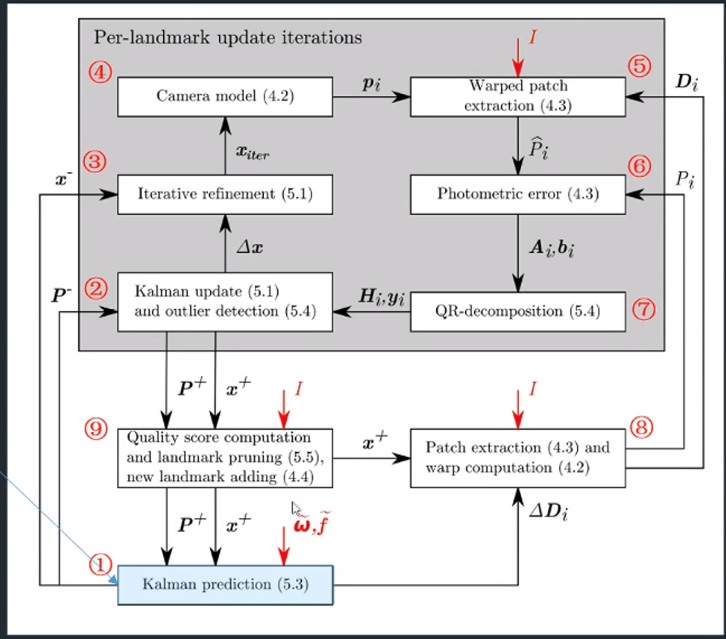
ROVIO使用光度误差
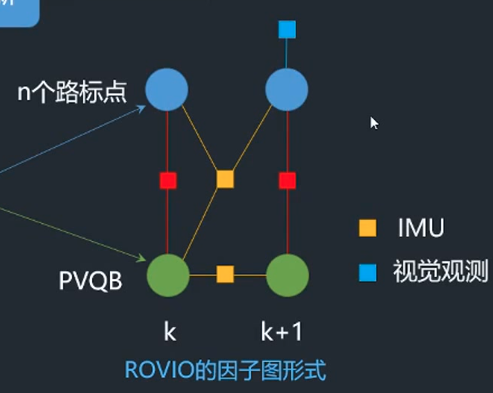
ROVIO将路标点包含到状态向量中。有因将路标点表征在当前帧的坐标系下,有范围限制,因此对其进行归一化得到无约束的状态量—方向向量Bearing Vector
ROVIO的创新点如下所示:
ROVIO中,路标点使用当前帧下的归一化相机系坐标Pc和你深度表示,并作为状态向量进行预测和更新。参数化不同导致预测和更新的细节不同,但总体还是EKF五大公式。又因Pc有边界约束,因此引入了Bearing Vector老了使得Pc平滑可导
状态向量:当前帧的PVQB和路标点( mu,p)
因子图如下
VINS
优化向量
包括滑动窗口内的n个相机状态PVQB、Camera到IMU的外参、m个3D点的逆深度:
$$
X=[x_0,x_1,…x_n,x_c^b,lambda_0,lambda_1,…lambda_m]
$$
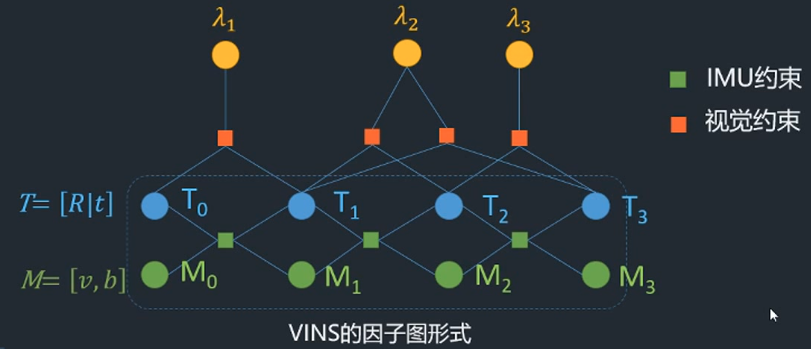
框表示滑动窗口,T中的R、t表示P、Q ;M中的是v和b;lambda表示路标的逆深度;(外参没有考虑)
VI-ORB
流程图
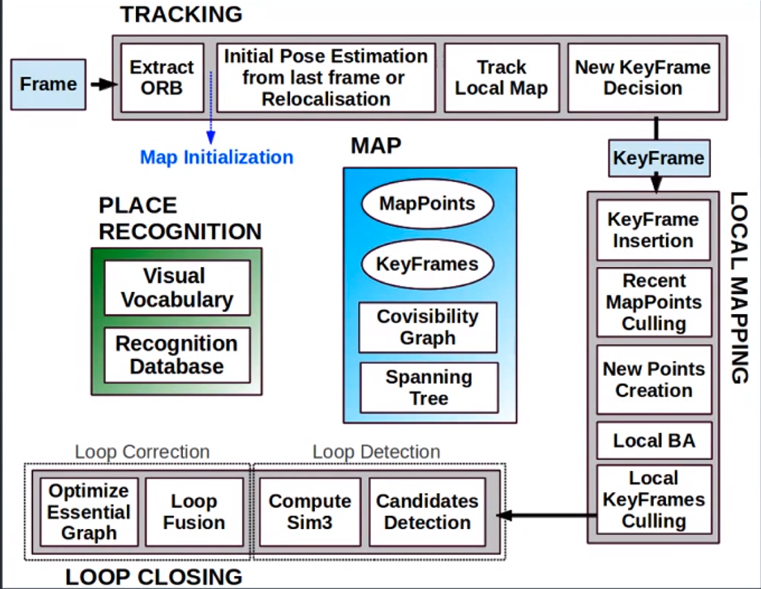
Tracklocal map:仅优化当前帧
Local Map:优化华创内的所有帧的PVQB和路标点
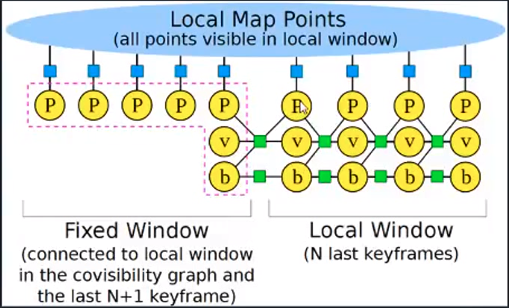
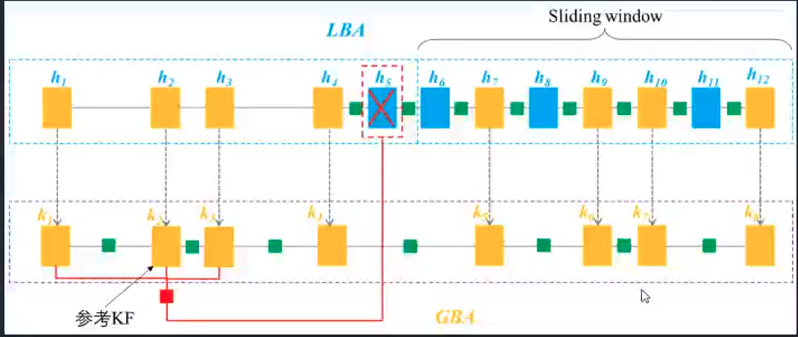
ICE-BA
增量式BA,误差为IMU和视觉,LBA为滑窗优化,GBA为所有KF优化,速度很快。

ICE-BA认为在建立增量方程时,对之前已经算过的且不变的那些状态向量没必要重新线性化(线性化及计算Jacobian),因为即使重新计算Jacobian也没什么变化。另外,也没必要对整体[H|b]矩阵进行消元,而是只对变化的进行更新。最后只计算变化的路标点即可。对于没有变化的状态向量的临时值则一直保存下来,避免重新计算。
总结而言,在ICE-BA中更新Factor有三种情况:
- 该Factor在本次迭代中没有变化,则不更新;
- 该Factor是新Factor,则在原来基础上+=新Factor。如新观察到一个新的路标点,则对此新路标点的观测约束就是一个新的Factor;
- 该Factor已存在但需要更新,则先减去旧Factor,再架上新Factor。