堆及其应用学习小结

堆及其应用

堆结构是一种数组对象，它可以被视为一棵完全二叉树。（如果一棵深度为K二叉树，1至k-1层的结点都是满的，即满足2i-1，只有最下面的一层的结点数小于2i-1，并且最下面一层的结点都集中在该层最左边的若干位置，则此二叉树称为完全二叉树。）
树中每个结点与数组中存放该结点中值的那个元素相对应：

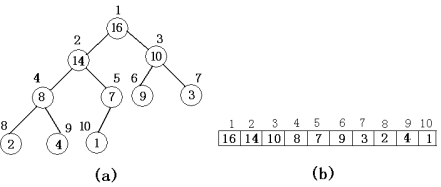
大根堆：除根节点外，父节点大，子节点依次减小；小根堆：除根节点外，父节点小，子节点依次增大。
堆的操作：用堆的关键部分是两个操作：put操作，即往堆中加入一个元素；get操作，即从堆中取出并删除一个元素。
Put:
在堆尾加入一个元素，并把这个结点置为当前结点,比较当前结点和它父结点的大小,如果当前结点小于父结点，则交换它们的值，并把父结点置为当前结点。重复这个过程直至单调结束。
若当前结点大于等于父结点，则不用调整。
Get:
（1）取出堆的根结点的值。
（2）把堆的最后一个结点（len）放到根的位置上，把根覆盖掉。把堆的长度减一。
（3）把根结点置为当前父结点pa。
（4）如果pa无儿子（pa>len/2），则转（6）；否则，把pa的两（或一） 个儿子中值最小的那个置为当前的子结点son。
（5）比较pa与son的值，如果fa的值小于或等于son，则转（6）；否则，交换这两个结点的值，把pa指向son，转（4）。
（6）结束。

int get() //heap[1]为堆顶
{
	int now=1, next, res= heap[1];
	heap[1] = heap[heap_size--];
	while(now * 2 <= heap_size)
	{
		next = now * 2;
		if (next < heap_size && heap[next + 1] < heap[next]) next++;
		if (heap[now] <= heap[next]) break;
		swap(heap[now], heap[next]);
		now = next;
	}
	return res;
}

使用C++标准模板库STL:

int get()
{
	//pop_heap(heap + 1, heap + heap_size + 1);               //大根堆
	pop_heap(heap + 1, heap + heap_size + 1, greater<int>());    //小根堆
	return heap[heap_size--];
}