[Swift]复数的表示和四则运算

★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★
➤微信公众号：山青咏芝（shanqingyongzhi）
➤博客园地址：山青咏芝（https://www.cnblogs.com/strengthen/ ）
➤GitHub地址：https://github.com/strengthen/LeetCode
➤原文地址：https://www.cnblogs.com/strengthen/p/9836010.html 
➤如果链接不是山青咏芝的博客园地址，则可能是爬取作者的文章。
➤原文已修改更新！强烈建议点击原文地址阅读！支持作者！支持原创！
★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★

我们把形如z=a+bi（a,b均为实数）的数称为复数，其中a称为实部，b称为虚部，i称为虚数单位。

当虚部等于零时，这个复数可以视为实数；当z的虚部不等于零时，实部等于零时，常称z为纯虚数。

复数域是实数域的代数闭包，也即任何复系数多项式在复数域中总有根。

复数是由意大利米兰学者卡当在十六世纪首次引入，

经过达朗贝尔、棣莫弗、欧拉、高斯等人的工作，此概念逐渐为数学家所接受。

用结构体来描述复数，复数由实部（real）和虚部（image）构成。

加法： (a+bi)+(c+di)=(a+c)+(b+d)i

减法： (a+bi)-(c+di)=(a-c)+(b-d)i

乘法：设z1=a+bi，z2=c+di(a、b、c、d∈R)是任意两个复数，那么它们的积(a+bi)(c+di)=(ac-bd)+(bc+ad)i

除法：满足(c+di)(x+yi)=(a+bi)的复数x+yi(x,y∈R)叫复数a+bi除以复数c+di的商。

          (a+bi)/(c+di)=(ac+bd)/(c2+d2) +((bc-ad)/(c2+d2))i

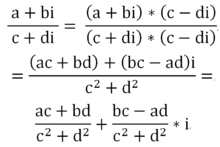
复数作为幂和对数的底数、指数、真数时，其运算规则可由欧拉公式e^iθ=cos θ+i sin θ（弧度制）推导而得

/*复数结构*/
struct Complex {
    //实部
    var real: Double    
    //虚部
    var img: Double  
    
    //将复数转换成字符串。
    var toString: String {
        //判断虚部是否大于0
        if img < 0
        {
            return "(real) - (-img)i"       
        }
        else if img > 0
        {
            return "(real) + (img)i"
        }
        else
        {
            return "(real)"
        }      
    }
    /*重载复数的四则运算符*/
    //重载加法运算符：(a+bi)+(c+di)=(a+c)+(b+d)i
    static func +(_ x: Complex,_ y: Complex) -> Complex {
        return Complex(real: (x.real + y.real), img: (x.img + y.img))
    }
    //重载减法运算符： (a+bi)-(c+di)=(a-c)+(b-d)i
    static func -(_ x: Complex,_ y: Complex) -> Complex {
        return Complex(real: (x.real - y.real), img: (x.img - y.img))
    }
    //重载乘法运算符
    //设z1=a+bi，z2=c+di(a、b、c、d∈R)是任意两个复数，那么它们的积(a+bi)(c+di)=(ac-bd)+(bc+ad)i
    static func *(_ x: Complex,_ y: Complex) -> Complex {
        return Complex(real: (x.real * y.real - x.img * y.img), img: (x.img * y.real + x.real * y.img))
    }
    //重载除法运算符
    //满足(c+di)(x+yi)=(a+bi)的复数x+yi(x,y∈R)叫复数a+bi除以复数c+di的商。
    //(a+bi)/(c+di)=(ac+bd)/(c2+d2) +((bc-ad)/(c2+d2))i
    static func /(_ x: Complex,_ y: Complex) -> Complex {
        var squares = pow(y.real,2) + pow(y.img,2)
        return Complex(real: (x.real * y.real - x.img * y.img) / squares, img: (x.img * y.real - x.real * y.img) / squares)
    }
    //复数的模：将复数的实部与虚部的平方和的正的平方根的值称为该复数的模。
    static func cbs(_ a: Complex) ->Double{
        return sqrt(pow(a.real,2) + pow(a.img,2))
    }
}

示例代码：

var c1 = Complex(real: 4, img: -8)
var c2 = Complex(real: 2, img: -2)

var sum = c1 + c2
print("(sum.toString)")
//Print 6.0 - 10.0i

var subtract = c1 - c2
print("(subtract.toString)")
//Print 2.0 - 6.0i

var product = c1 * c2
print("(product.toString)")
//Print -8.0 - 24.0i

var quotient = c1 / c2
print("(quotient.toString)")
//Print -1.0 - 1.0i

var mould = Complex.cbs(c1)
print("(mould) ")
//Print 8.94427190999916