（基础）--- 约数

试除法求约数

循环到n/i,存入i与n/i，若i == n/i，则只存一个

#include<iostream>
#include<algorithm>
#include<vector>

using namespace std;

int n;

vector<int > get_divisors(int n){
	vector<int> res;
	
	for(int i = 1; i <= n/i; i ++ ){
		if( n % i == 0){
			res.push_back(i);
			if( i != n/i) res.push_back(n/i);
		}
	}
	sort(res.begin(),res.end());
	return res;
}
int main() {
	cin>>n;
	
	while(n -- ){
		int x; cin >> x;
		auto res = get_divisors(x);
		for(auto t : res) cout<<t<<" ";
		puts("");
	}
	return 0;
}

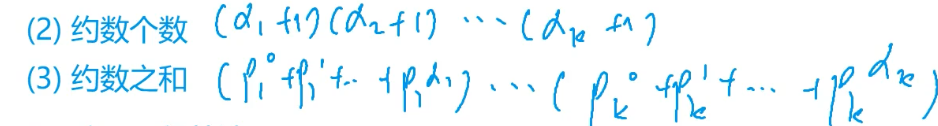
约数个数

#include<iostream>
#include<algorithm>
#include<unordered_map>

using namespace std;

typedef long long LL;

const int mod = 1e9+7;
int main(){
	int n;
	cin >> n;
	
	unordered_map<int,int> primes;
	while(n --){
		int x; cin >> x;
		
		for(int i = 2; i <= x/i; i ++ ){
			while( x % i == 0){
				x /= i;
				primes[i] ++;
			}
		}
		if(x > 1) primes[x] ++;
	}
	LL res = 1;
	for(auto prime : primes) res = res * (prime.second + 1) % mod;
	
	cout<<res<<endl;
	
	return 0;
} 

约数之和

#include<iostream>
#include<algorithm>
#include<unordered_map>

using namespace std;

typedef long long LL;

const int mod = 1e9+7;
int main(){
	int n;
	cin >> n;
	
	unordered_map<int,int> primes;
	while(n --){
		int x; cin >> x;
		
		for(int i = 2; i <= x/i; i ++ ){
			while( x % i == 0){
				x /= i;
				primes[i] ++;
			}
		}
		if(x > 1) primes[x] ++;
	}
	LL res = 1;
	for(auto prime : primes){
		int p = prime.first, a = prime.second;
		LL t = 1;
		while(a -- ) t = (t * p + 1) % mod;
		res = res * t % mod;
	}	
	
	cout<<res<<endl;
	
	return 0;
} 

最大公约数

欧几里得原理：辗转相除法

int gcd(int a,int b){
            
	return b?gcd(b,a%b):a;
}
or
int gcd(int a,int b){
	if(b==0)
	return a;
	else 
	return gcd(b,a%b);
	
}