【线段树+扫描线】P5490 【模板】扫描线

P5490 【模板】扫描线

首先有这么一张图，要求它的面积并。

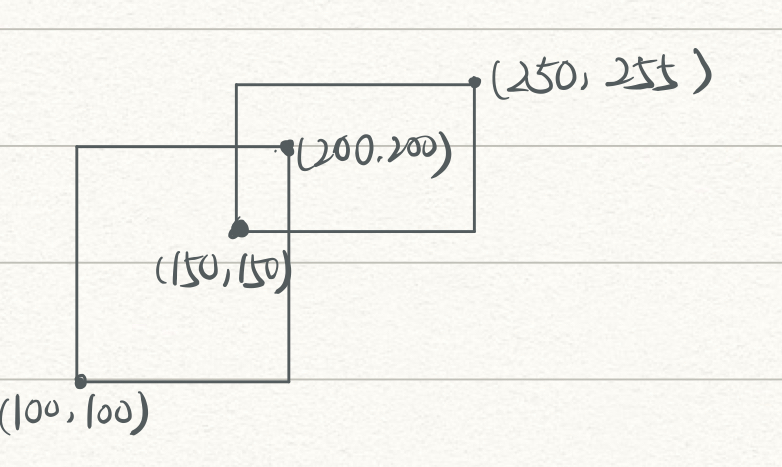
我们想，如果可以有一条扫描线从下往上扫，记录它所扫到的边的长度（并）(len)，再求出这条边与即将扫到的下一条边的距离(h)，那么我们就可以求出第一块面积（紫色）(S_1=len imes h)

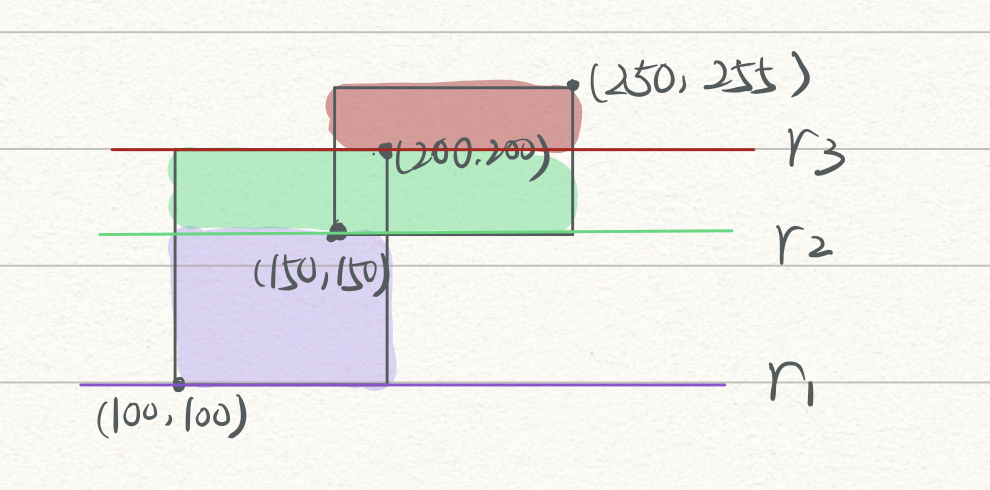
然而如何求出这个(len)？

显然只用当前边的长度是不行的，如：当扫到边(r_2)的时候，(len)应该是(250-100=150)这么长

什么情况下应该把之前扫过的边的长度也考虑进去？

我们注意到，当一个矩形只有下边被扫过的时候，对这个矩形的面积计算仍未结束，那么这个矩形的下边长度应该被算进(len)中。当这个矩形的上边被扫过之后，它的下边长度不需要再考虑到(len)中了。

因此我们需要对矩形的上下边进行区分：将下边标记为1，上边标记为-1。

当扫到边(r_2)时，(r_2)与(r_1)有重叠部分。新的问题又来了：如何不重不漏地计算这个(len)？

我们将所有矩形的端点投影到x轴上，结果如下图：

当扫到边(r_1)时，区间[x1,x2]与[x2,x3]被覆盖了。我们记录下区间的被覆盖次数。

当扫到边(r_2)时，区间[x2,x3]与[x3,x4]被覆盖了。这时区间的被覆盖次数：

(cnt_{[x1,x2]}=1)，(cnt_{[x2,x3]}=2)，(cnt_{[x3,x4]}=1)。

那么我们只需要统计(cnt)是正数的区间，然后将这些区间的长度相加即可得到(len)。

此时(len=L_{[x1,x2]}+L_{[x2,x3]}+L_{[x3,x4]}=150)。

(r_2)与下一条边的距离(h=50)，则第二块面积​（绿色）(S_2=len imes h)

当扫到边(r_3)时，我们知道这是左边那个矩形的上边，它的标记是-1。

被它覆盖的区间有[x1,x2]和[x2,x3]。

遇到(r_3)意味着我们不再需要考虑(r_1)的长度了，如何在计算中体现这个“不再考虑”？很简单，因为我们之前统计过区间的被覆盖次数，“不再考虑”时将对应区间的覆盖次数扣除（-1）即可。

更新之后，区间的被覆盖次数如下：

(cnt_{[x1,x2]}=0)，(cnt_{[x2,x3]}=1)，(cnt_{[x3,x4]}=1)。

同样，我们再一次统计(cnt)是正数的区间，然后将这些区间的长度相加即可得到(len)。

此时(len=L_{[x2,x3]}+L_{[x3,x4]}=100)。

(r_3)与下一条边的距离(h=55)，则第三块面积（红色）(S_3=len imes h)

我们知道(r_4)是整个图里剩下的最后一条与x轴平行的边，所以当扫描线扫过(r_3)时，面积计算就结束了，不需要再扫过(r_4)。

那么最后的面积并(ans=S_1+S_2+S_3)

过程捋清楚了，那么落实到代码上，又应该用什么数据结构来储存最关键的、由所有矩形的端点在x轴上的投影所划分出的区间呢？

在上述过程中，我们的计算都是具体到如[x1,x2]、[x2,x3]这样的最小区间。这显然是可优化的：例如，在扫描到r_3时，可以只在[x1,x3]这个更大区间上作统计，而不必进一步细分。

这样的性质可以联想到线段树。

在模板线段树中，一个结点代表的是区间([l,r])上的若干个点。特别地，在叶子结点中(l=r)，此时([l, r ])代表的是1个点。

本题要求我们线段树存的是线段，不能是点。所以我们改变结点的定义：结点([l,r])代表的是线段([l,r+1])。如此，线段树的叶子节点([l,r](l=r))代表的就是最小的区间，如([x_1,x_2])、([x_4,x_5])这样的区间。

还有一个问题：离散化。考虑题目中的数据范围：1e9，显然这要求我们对所有矩形的端点的x值进行离散化（也就是重新编号）。再将实际x值储存到离散化后对应下标即可，如X[1]=100,X[2]=150.

struct Tree{
	int l,r,cnt,len;
}tree[maxn*4];

建树过程和模板线段树区别不大：

void build(int i,int l,int r){
	tree[i].l=l;
	tree[i].r=r;
	if(l==r) return;
	int mid=(l+r)>>1;
	build(i*2,l,mid);
	build(i*2+1,mid+1,r);
}

扫描到新的一条与x轴平行的边后的对len的更新操作（最后的更新结果是tree[1].len）：

void update(int i){
	int l=tree[i].l,r=tree[i].r;
	if(tree[i].cnt) tree[i].len=X[r+1]-X[l];
  //如果tree[i]所代表的区间被矩形完全覆盖，直接计算该区间的长度
	else{
		tree[i].len=tree[i*2].len+tree[i*2+1].len;
    //不完全覆盖/没有覆盖，用其子结点的长度并
	}
}

void change(int i,LL L,LL R,int c){
  //L、R是真实区间
  //l,r仅为端点下标
	int l=tree[i].l,r=tree[i].r;
	if(X[r+1]<=L||X[l]>=R) return;
  //如果下标所代表的区间完全不在[L,R]范围内，就返回
  if(X[l]>=L&&X[r+1]<=R){
    //如果下标所代表的区间被[L,R]完全覆盖
    tree[i].cnt+=c;
    //更新被覆盖次数
    update(i);
    //计算新的len
    return;
  }
  //如果下标代表的区间被[L,R]部分覆盖，找子结点，再计算新的len
  change(i*2,L,R,c);
  change(i*2+1,L,R,c);
  update(i);
}

struct ScanLine{
	LL l,r,h;
	//保存线的左右端点（下标），及其高度(y值)
	int mark;
	//保存线的权值
	bool operator < (const ScanLine &t) const{
		return h<t.h;
		//按y值从小到大排序
	}
}line[maxn*2];
//line数组保存所有与x轴平行的线的信息

完整代码如下：

typedef long long LL;
const int maxn = 1000000 + 10;
LL n, x, y, xx, yy;
LL X[maxn * 2];

struct ScanLine {
    LL l, r, h;
    int mark;
    bool operator < (const ScanLine& t)const {
        return h < t.h;
    }
}line[maxn*2];

struct Tree {
    int l, r, cnt;
    LL len;
}tree[maxn*4];

void build(int i, int l, int r) {
    tree[i].l = l;
    tree[i].r = r;
    if (l == r) return;
    int mid = (l + r) >> 1;
    build(i * 2, l, mid);
    build(i * 2 + 1, mid + 1, r);
}

void update(int i) {
    int l = tree[i].l;
    int r = tree[i].r;
    if (tree[i].cnt) tree[i].len = X[r + 1] - X[l];
    else {
        tree[i].len = tree[i * 2].len + tree[i * 2 + 1].len;
    }
}

void change(int i, LL L, LL R, int m) {
    int l = tree[i].l;
    int r = tree[i].r;
    if (X[l] >= R || X[r + 1] <= L) return;
    if (X[l] >= L && X[r + 1] <= R) {
        tree[i].cnt += m;
        update(i);
        return;
    }
    change(i * 2, L, R, m);
    change(i * 2 + 1, L, R, m);
    update(i);
}

int main()
{
    //ios::sync_with_stdio(false);
    //while (scanf("%d%d",&n,&m)!=EOF){
    cin >> n;
    for (int i = 1; i <= n; i++) {
        cin >> x >> y >> xx >> yy;
        X[2 * i - 1] = x;
        X[2 * i] = xx;
      //注意这里已经完成了离散化的第一步：重编号
        ScanLine t;
        t.l = x; t.r = xx; t.h = y; t.mark = 1;
        line[2 * i - 1] = t;
        t.h = yy; t.mark = -1;
        line[2 * i] = t;
    }
  //显然我们读入了2*n条边
    n *= 2;
    sort(line + 1, line + n + 1);
  //将所有线从低到高排序
    sort(X + 1, X + n + 1);
    int tail = unique(X + 1, X + n + 1) - (X + 1);
  //离散化第二步：去重（unique函数要求数组有序）
    build(1, 1, tail - 1);
  //考虑线段树结点的定义，就知道最右边那个端点不应该包含在内
  //故范围是1到tail-1
    LL ans = 0;
    //从下往上扫
    for (int i = 1; i < n; i++) {
        change(1, line[i].l, line[i].r, line[i].mark);
        ans += tree[1].len * (line[i + 1].h - line[i].h);
        //len的最终更新结果在tree[1]中
    }
    cout << ans;
    return 0;
}