【CF1491G】Switch and Flip

题目

题目链接：https://codeforces.com/contest/1491/problem/G
桌面上有 (n) 枚硬币。初始时，第 (c_i) 号硬币位于位置 (i)，正面朝上（(c_1, c_2, cdots, c_n) 是一个 (1 sim n) 的排列）。你可以对这些硬币做一些操作。每次操作，你可以如下进行：

• 选择两个不同的 (i) 和 (j)。
• 交换位于 (i) 和 (j) 的两枚硬币。
• 把位于 (i) 和 (j) 的两枚硬币分别翻转。

你可以进行不超过 (n + 1) 次操作，使得第 (i) 号硬币位于位置 (i)，且都是正面朝上。
你不需要最小化操作的次数，输出任意一种方案即可。
(nleq 2 imes 10^5)。

思路

根据位置 (i) 要去的位置 ( ext{nxt}[i])，我们可以建出一张图，第 (i) 条有向边是 ((i, ext{nxt}[i]))。
显然图构成了若干个环，为了让操作次数 (leq n+1)，一个大小为 (k) 的环肯定是要在 (k) 步内搞定。
考虑任意两个环，我们分别取两个环上的点 (a,b)，交换 (a,b) 后两个环就会合并成一个环。
抠一张 CF 题解的图，其中红色是未翻转，蓝色是已翻转：

之后我们一直交换蓝点和它的下一个点，直到它的下一个点是另一个蓝点。
那么最后一定是两个蓝点形成一个大小为 (2) 的环，以及若干个红点单独成环。再交换一次两个蓝点即可。
操作次数恰好是两个环的大小之和。
那么如果环的总数是奇数个应该如何处理剩下的一个环呢？
如果环的数量大于 (1)，可以直接把剩下一个环和之前任意一个已经形成大小为 (1) 的环进行操作，会额外产生 (1) 的贡献，总操作次数是 (n+1)。
如果环的数量等于 (1)，那么环的大小 (geq 3)。可以手玩出环大小为 (3) 的情况：

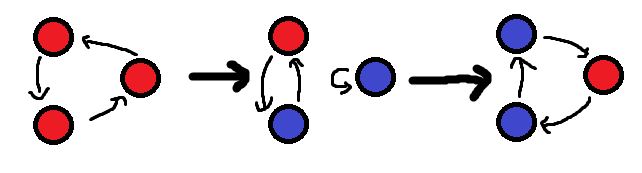
如果环的大小大于 (3)，那么我们就可以从任意一个点 (i) 开始，不断交换 (i) 和 ( ext{nxt}[i])，直到环的大小为 (3)。此时这个环上的点一定是上图中第二种情况再加上若干个单独成环的红点。那么用大小等于 (3) 的方法解决即可。操作次数依然是 (n+1)。

代码

#include <bits/stdc++.h>
#define mp make_pair
#define ST first
#define ND second
using namespace std;

const int N=200010;
int n,last,nxt[N];
bool vis[N];
queue<pair<int,int> > q;

void change(int i,int j)
{
	q.push(mp(i,j));
	swap(nxt[i],nxt[j]);
}

void solve(int i,int j)
{
	change(i,j);
	while (nxt[i]!=j) change(i,nxt[i]);
	while (nxt[j]!=i) change(j,nxt[j]);
	change(i,j);
}

int main()
{
	scanf("%d",&n);
	for (int i=1;i<=n;i++)
		scanf("%d",&nxt[i]);
	for (int i=1;i<=n;i++)
		if (!vis[i])
		{
			for (int j=i;!vis[j];j=nxt[j]) vis[j]=1;
			if (!last) last=i;
				else solve(last,i),last=0;
		}
	if (last==1)
	{
		int i=last,j=nxt[last];
		while (nxt[nxt[i]]!=i) change(i,nxt[i]);
		int k=nxt[i];
		change(j,k); change(i,k); change(i,j);
	}
	if (last>1) solve(1,last);
	cout<<q.size()<<"
";
	for (;q.size();q.pop())
		cout<<q.front().ST<<' '<<q.front().ND<<"
";
	return 0;
}