hdu 6069 Counting Divisors（求因子的个数）

Counting Divisors

Time Limit: 10000/5000 MS (Java/Others)    Memory Limit: 524288/524288 K (Java/Others)
Total Submission(s): 3170    Accepted Submission(s): 1184

Problem Description

In mathematics, the function d(n) denotes the number of divisors of positive integer n.

For example, d(12)=6 because 1,2,3,4,6,12 are all 12's divisors.

In this problem, given l,r and k, your task is to calculate the following thing :

(∑i=lrd(ik))mod998244353

Input

The first line of the input contains an integer T(1≤T≤15), denoting the number of test cases.

In each test case, there are 3 integers l,r,k(1≤l≤r≤1012,r−l≤106,1≤k≤107).

Output

For each test case, print a single line containing an integer, denoting the answer.

 

Sample Input

3

1 5 1

1 10 2

1 100 3

 

Sample Output

10

48

2302

 

Source

2017 Multi-University Training Contest - Team 4

Recommend

liuyiding   |   We have carefully selected several similar problems for you:  6119 6118 6117 6116 6115 

 

题目大意：

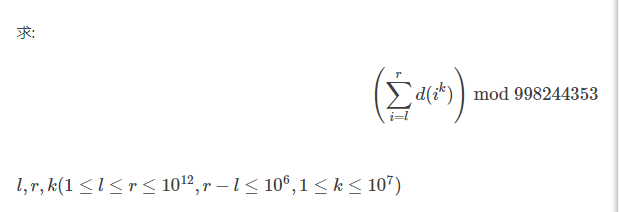
求   l<= t <=r,  求   对多有满足条件的t 的   d(t^k)=t^k的所有因子的个数    的总和

 

题解：

根据约数个数定理：n=p1^a1×p2^a2×p3^a3*…*pk^ak,n的约数的个数就是(a1+1)(a2+1)(a3+1)…(ak+1).

只要求1～1e6之间的素数，如果当某个数除完前面的素数的时候还！=1，那么那个数字就是>1e6的素数。

 

#include <iostream>
#include<cstdio>
#include<algorithm>
#include<queue>
#include<map>
#include<vector>
#include<cmath>
#include<cstring>
#include<bits/stdc++.h>

using namespace std;
const long long mod=998244353;
long long ans,l,r,k,len;
int T;
long long f[100000],num[1000005],a[1000005];
void pre()
{
    bool flag;
    len=0;
    f[++len]=2;
    for(int i=3;i<=1e6;i++)
    {
        flag=1;
        for(int j=2;j<=sqrt(i);j++)
        if (i%j==0) {flag=0; break;}
        if (flag) f[++len]=i;
    }
    return;
}

int main()
{
    pre(); //预处理出1～1e6之间的素数
    scanf("%d",&T);
    for(;T>0;T--)
    {
        scanf("%lld%lld%lld",&l,&r,&k);
        for(int i=0;i<=r-l;i++) {num[i]=1; a[i]=i+l;}  //num【i】表示 i 这个数的因子个数
        ans=0;
        for(int i=1;i<=len;i++)
        {
            long long s=(l/f[i])*f[i];
            if (s<l) s+=f[i];
            for(long long j=s;j<=r;j+=f[i])
            {
                long long w=0;
                while(a[j-l]%f[i]==0)
                {
                    a[j-l]/=f[i];
                    w++;
                }
                num[j-l]=num[j-l]*(w*k+1)%mod;
            }
        }
        for(int i=0;i<=r-l;i++)
            if (a[i]>1) num[i]=num[i]*(k+1)%mod;  //特殊判断还剩下的数字！=1的情况，也就是还有一个大素数

        for(int i=0;i<=r-l;i++) ans=(ans+num[i])%mod;
        printf("%lld
",ans);
    }
    return 0;
}