本文塞得很满(!),如有错误欢迎指出~
Upd 2020-07-29:(KM)还以为是板子错了,后来才发现是HDU2853题目里两个集合的数量不同,而之前写的题目两个集合都是相同的就没改动板子。现已把该题目加入本文中!
二分图及其经典匹配问题
简介
二分图又称作二部图,是图论中的一种特殊模型。 设(G=(V,E))是一个无向图,如果顶点(V)可分割为两个互不相交的子集((A,B)),并且图中的每条边((i,j))所关联的两个顶点(i)和(j)分别属于这两个不同的顶点集((i in A,j in B)),则称图(G)为一个二分图。 ——百度百科 - 《二分图》
简单来说就是这张图中共有两个集合(U、V),图上的点属于两集合其一。相同集合中的点之间没有互相关系,不同集合的点可能会有关系(连线)。故这种图经常被视为夫妻匹配图(emm某些特殊关系在这就当作没有吧)。如下图所示
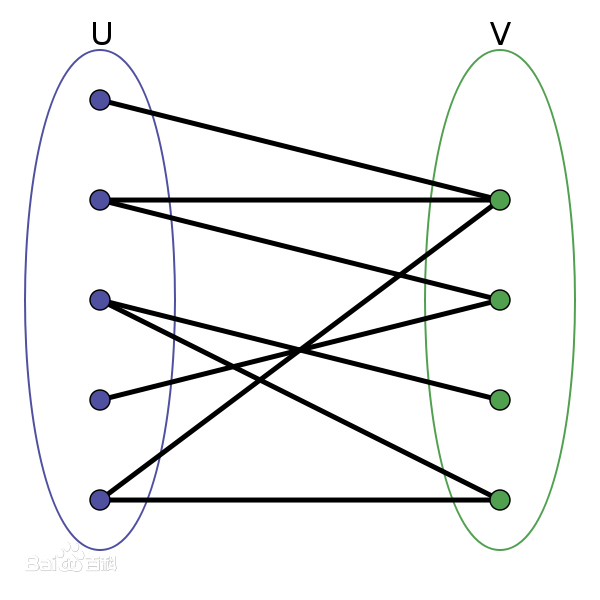
二分图最大匹配
二分图最大匹配,顾名思义就是一个点最多只能有与其有关系的一条边被选中,问最多能选择多少条边
换作夫妻匹配问题,就是问在一夫一妻制下最多能找到多少对海王夫妻
著名的解决二分图最大匹配问题的算法为匈牙利算法,也可以借助最大流/最小割模型解决这类问题
二分图最大权完美匹配
二分图最大权完美匹配,表示此时的二分图的边是带有边权的
与二分图最大匹配不同的是,最大权完美匹配侧重于最大权值,要求在保证一个点最多只能有与其有关系的一条边被选中的前提下,选出的边的边权总和最大
换做夫妻匹配问题,同样以一夫一妻制为背景,但此时男女生之间存在一种叫好感度的数值,要求好感度总和最大
著名的解决二分图最大权完美匹配问题的算法为KM算法
匈牙利(Hungary)算法
引入
匈牙利算法是基于深度优先搜索一遍一遍搜索增广路的存在性来增加匹配对数的
我们将问题看作相亲现场,每个(U)集合的人排队寻找(V)集合里的对象
假设是男生排队找女生,基于这个"时间"顺序,假设前面的男生已经匹配了一些
下一个男生(a)进来匹配,算法便会遍历一遍他认识的女生(与他有关系的(V)集内的点)
如果发现当前遍历到的女生还没有被其他男生匹配,那非常好,就直接把这个女生匹配给男生(a)
如果发现已经被其他男生(b)给绿匹配了,那算法会尝试去和那个男生(b)沟通,询问能否让他换一个(?)
算法便会来到那个男生(b)那里,重新遍历一遍他认识的女生,看看能否找到其他能够匹配的女生(寻找增广路/套娃)
如果可以,那么男生(b)便会与新找到的女生匹配,顺利成章的,原来与男生(b)匹配的女生就可以和男生(a)匹配啦
如果不行,那么男生(a)就没这个机会了QAQ,尝试下一个吧(继续遍历),实在不行(遍历完了)单着挺好的
就以这样的方法一直搜索,直到所有男生((U)集)该匹配的都匹配完了,就能得到最大匹配数了
(但是这样找女朋友真的好吗qwq,好的话给我也整一个)
代码实现
下面使用(vector G)来储存每个男生认识的女生
使用(int match)来储存每个女生当前匹配的男生的编号(没匹配则为(0))
如上面所说,我们需要遍历每个(U)集的男生去尝试匹配
对于每个男生(p),要遍历一遍他认识的女生
for(int i:G[p])
此时女生的编号便以(i)来表示
如果当前的女生没被匹配到,自然可以直接让她与当前的男生(p)进行匹配
但如果已经被匹配过,则尝试让匹配她的那个男生去再找找看其他女生(开始套娃),如果返回(true)也可以正常匹配
for(int i:G[p])
{
if(!match[i]||hungary(match[i]))
{
match[i]=p;
return true;
}
}
那么对于这个套娃应该如何处理呢
每次搜索时都假设自己没匹配到,那么上面的代码可以满足搜索的功能
但是可以发现一个问题,从第二层寻找增广的搜索开始,(match)数组的值是没有变的(也就是说在寻找到新的女生之前,第一层遍历到的那个女生的(match)依旧是第二层的这个男生)
第二层这个男生一定还会再找到这个女生,于是便会开始无限套娃死循环(Runtime Error)
所以我们需要新开一个数组(vis)来储存当前这一遍搜索是否已经让某个男生找过增广路了(找过了就不用再找了反正也找不到,正在找的话就直接退出防止套娃)
至此这个搜索函数算是完整了
bool hungary(int p)
{
if(vis[p]) //防止套娃
return false;
vis[p]=true; //访问标记
for(int i:G[p])
{
if(!match[i]||hungary(match[i]))
{
match[i]=p;
return true; //海王在世
}
}
return false; //单身贵族
}
但是先这样使用(bool vis)的话有个弊端,也就是每次搜索某个男生时都要清空一次,时间耗费总和挺大的
所以我们可以在传值的时候再加个趟数(op),表示这是第几趟匹配了(或者表示这一趟主要是为了让哪个男生找女生),这样使用(int vis)便可以做到不清空解决问题
bool hungary(int p,int op) //新增传值
{
if(vis[p]==op) //依据趟数防止套娃
return false;
vis[p]=op; //标记这一趟是否访问过
for(int i:G[p])
{
if(!match[i]||hungary(match[i],op))
{
match[i]=p;
return true;
}
}
return false;
}
完整程序
时间复杂度为(O(nm))
#include<bits/stdc++.h>
using namespace std;
const int N=555;
vector<int> G[N];
int match[N],vis[N];
bool used[N][N];
bool hungary(int p,int op)
{
if(vis[p]==op)
return false;
vis[p]=op;
for(int i:G[p])
{
if(!match[i]||hungary(match[i],op))
{
match[i]=p;
return true;
}
}
return false;
}
int main()
{
int n,m,e,a,b;
scanf("%d%d%d",&n,&m,&e);
while(e--)
{
scanf("%d%d",&a,&b);
if(used[a][b]) //判重边
continue;
used[a][b]=true;
G[a].push_back(b);
}
int ans=0;
for(int i=1;i<=n;i++)
if(hungary(i,i))
ans++;
printf("%d
",ans);
return 0;
}
Dinic最小割 / 最大流
建图法
由于一个点最多只能匹配到一条边
每条边又表示着两点间存在关系
所以可以建立一个超级源点(S)以及超级汇点(T)
将(U)集与(V)集分散在两列(也就是上面的二分图图示)
(S)与(U)集合每个点建立一条边,流量为(1),表示每个人最多只能被(1)条边匹配到
同样的,(V)集合每个点与(T)建立一条边,流量为(1)
最后,如果(U)集中点(a)与(V)集中点(b)之间存在关系(可匹配性)
就建立一条(a)至(b)的边,流量也为(1)
这样就相当于增广路的条数就是二分图的最大匹配
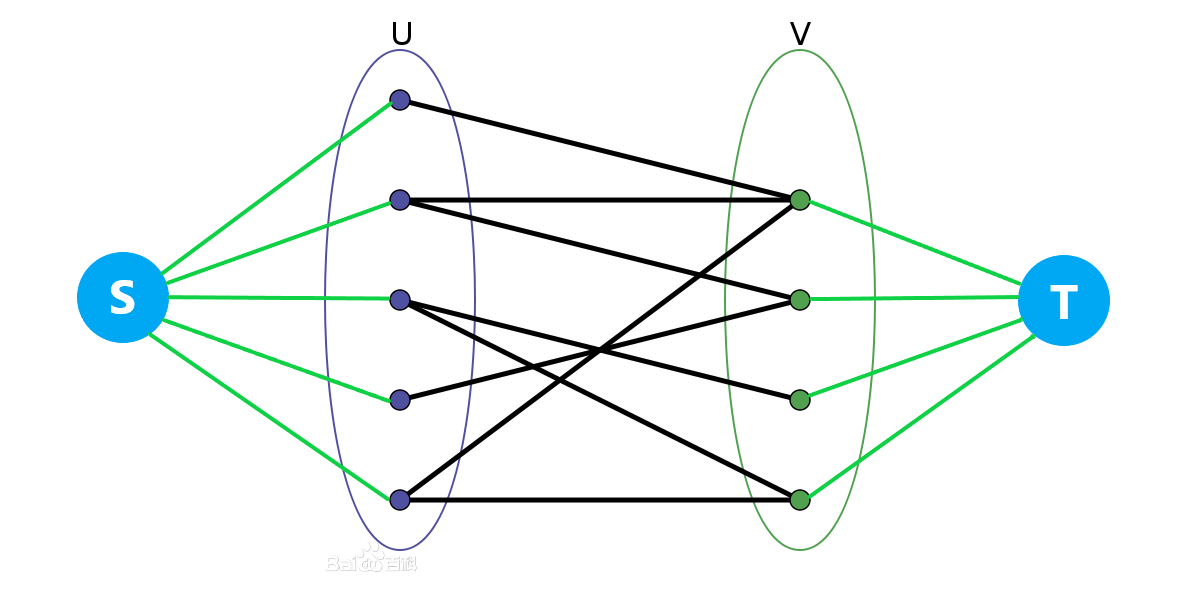
完整程序
时间复杂度应该为(O(nm^2))
#include<bits/stdc++.h>
using namespace std;
const int INF=0x3f3f3f3f;
const int maxn=510;
const int maxm=50050;
struct edge{
int u,v,cap,flow;
edge(){}
edge(int u,int v,int cap,int flow):u(u),v(v),cap(cap),flow(flow){}
}eg[maxm<<1];
int tot,s,t,dis[maxn<<1],cur[maxn<<1];
vector<int> tab[maxn<<1];
void addedge(int u,int v,int cap)
{
tab[u].push_back(tot);
eg[tot++]=edge(u,v,cap,0);
tab[v].push_back(tot);
eg[tot++]=edge(v,u,0,0);
}
int bfs()
{
queue<int> q;
q.push(s);
memset(dis,INF,sizeof dis);
dis[s]=0;
while(!q.empty())
{
int h=q.front(),i;
q.pop();
for(i=0;i<tab[h].size();i++)
{
edge &e=eg[tab[h][i]];
if(e.cap>e.flow&&dis[e.v]==INF)
{
dis[e.v]=dis[h]+1;
q.push(e.v);
}
}
}
return dis[t]<INF;
}
int dfs(int x,int maxflow)
{
if(x==t||maxflow==0)
return maxflow;
int flow=0,i,f;
for(i=cur[x];i<tab[x].size();i++)
{
cur[x]=i;
edge &e=eg[tab[x][i]];
if(dis[e.v]==dis[x]+1&&(f=dfs(e.v,min(maxflow,e.cap-e.flow)))>0)
{
e.flow+=f;
eg[tab[x][i]^1].flow-=f;
flow+=f;
maxflow-=f;
if(maxflow==0)
break;
}
}
return flow;
}
int dinic()
{
int flow=0;
while(bfs())
{
memset(cur,0,sizeof(cur));
flow+=dfs(s,INF);
}
return flow;
}
bool vis[555][555];
int main()
{
int n,m,e,a,b;
scanf("%d%d%d",&n,&m,&e);
tot=0,s=1001,t=1002;
for(int i=1;i<=n;i++)
addedge(s,i,1);
for(int i=501;i<=500+m;i++)
addedge(i,t,1);
while(e--)
{
scanf("%d%d",&a,&b);
if(vis[a][b])
continue;
vis[a][b]=true;
addedge(a,b+500,1);
}
printf("%d
",dinic());
return 0;
}
KM算法
引入
KM算法解决的“二分图最大权完美匹配”问题是“二分图最大匹配”进阶而来,但所求存在共通点
所以KM算法是套在匈牙利算法之上的一个算法,它也需要匈牙利算法那样一遍一遍寻找增广路从而求出最优解
在“二分图最大权完美匹配”问题中,每条边存在一个边权(favor[i][j])
同时我们还需要一些数组——
(val1[N]/val2[N])分别记录(U)集与(V)集点的点权(匹配期望值)
(vis1[N]/vis2[N])分别记录每次寻找增广路过程中(U)集与(V)集点的访问情况
(match[N])记录最终(U)集内点匹配到的在(V)集内点的编号
(slack[N])记录匹配过程中,(U)集内任意点能够选择(V)集内任意点作为匹配对象所需要降低(val)(期望值)的最小值
一些参考书即其它博客的较为规范的名称定义为:
(val1[N]/val2[N])为顶标,且满足(val1[i]+val2[j]≥w[i][j])
满足(val1[i]+val2[j]=favor[i][j])的边((i,j))称为相等边
由上述相等边构成的子图为相等子图
由增广路径构成的树为交错树
故KM算法的结论为:若由二分图中所有满足(A[i]+B[j]=w[i,j])的边((i,j))构成的子图(称做相等子图)有完备匹配,那么这个完备匹配就是二分图的最大权匹配。
理论很绕且难懂,所以下面就继续相亲(?
将此时的(val1/val2)看作是与该点进行匹配的期望值
初始化(val1[i])为(i)相邻边权的最大值(即每次匹配女生都是从权值最大的开始)
如果匹配可以直接成功,就将(match[i])的指向确定下来
如果不能,说明需要降低(val1)的期望继续寻找匹配
KM算法的关键点在于,如果在匹配男生(p)时,遍历(V)集寻找女生,发现女生(i)与其无法匹配((val1[p]+val2[i]≠favor[p][i])),可能是不存在连边(能够排除),也可能是某一方期望值曾发生过改变,则会将“如果让这个男生与这个女生匹配还需要的期望值”取小存在(slack[i])中
当本次匹配失败时,将会在所有(tmp)中再取小,让所有访问过的男生期望值降低,让所有访问过的女生期望值增加
正是最后这个“全部再取小”再去改变期望值,才能保证在某次匹配成功时,期望值理论变化最低,使得二分图此时的权和是最大的
总而言之,算法是遍历(U)集内所有点,循环进行如下操作
- 设置最大期望值
- 利用匈牙利算法找增广路
- 找到增广路,匹配成功,退出
- 找不到,最小程度降低男生期望,提升女生期望
- 继续回到(2)开始重复
另外,需要保证每次进行匈牙利算法时,每个女生只访问一次
完整程序(DFS)
该算法最坏情况时间复杂度为(O(n^4))
所以下面的代码在该题(6-10)测试点将会TLE
但在平时的题目中一般不会卡复杂度
两集合数量相同情况
以Luogu P6577 - 【模板】二分图最大权完美匹配为例
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int INF=0x3f3f3f3f;
const int N=510;
int n,m,match[N];
bool vis1[N],vis2[N];
ll favor[N][N],val1[N],val2[N],slack[N];
bool dfs(int p)
{
vis1[p]=true; //标记本次匹配涉及多少男生尝试进行换女生
for(int i=1;i<=n;i++)
if(!vis2[i]) //保证每次寻找增广路在V集中的点只访问一次
{
if(val1[p]+val2[i]==favor[p][i]) //男生与女生存在着连线(即这两人可以进行匹配)
{
vis2[i]=true;
if(!match[i]||dfs(match[i])) //匈牙利算法,寻找增广路
{
match[i]=p;
return true;
}
}
else
slack[i]=min(slack[i],val1[p]+val2[i]-favor[p][i]); //否则将男生与女生匹配还需要的期望值取小存入slack中
}
return false;
}
ll KM()
{
for(int i=1;i<=n;i++)
{
val1[i]=-INF;
for(int j=1;j<=n;j++)
val1[i]=max(val1[i],favor[i][j]); //初始val1的值为与其相邻边权的最大值
}
for(int i=1;i<=n;i++)
{
while(true) //只要没找到匹配,就降低期望值一直找下去
{
memset(vis1,false,sizeof vis1);
memset(vis2,false,sizeof vis2);
memset(slack,INF,sizeof slack);
if(dfs(i))
break; //如果能找到匹配就退出
ll d=INF; //找不到就减少期望值继续找
for(int j=1;j<=n;j++)
if(!vis2[j])
d=min(d,slack[j]); //在所有未访问过的女生匹配所需期望值再取小(最大程度减少换人匹配的期望损耗)
for(int j=1;j<=n;j++)
{
if(vis1[j])
val1[j]-=d; //如果是上一趟匹配访问过的男生,就降低他的期望值
if(vis2[j])
val2[j]+=d; //如果是上一趟匹配访问过的女生,就增加她的期望值
}
}
}
ll res=0;
for(int i=1;i<=n;i++)
res+=favor[match[i]][i]; //最后将对应匹配的边权求和输出
return res;
}
int main()
{
int u,v;
ll w;
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
favor[i][j]=-INF;
for(int i=1;i<=m;i++)
{
scanf("%d%d%lld",&u,&v,&w);
favor[u][v]=max(favor[u][v],w);
}
printf("%lld
",KM());
for(int i=1;i<=n;i++)
printf("%d ",match[i]);
return 0;
}
两集合数量不同情况
以HDU 2853为例,要注意每个循环是以(U)集为底还是以(V)集为底
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int INF=0x3f3f3f3f;
const int N=55;
int n,m,match[N]; //n为男生数量,m为女生数量
bool vis1[N],vis2[N];
ll favor[N][N],val1[N],val2[N],slack[N];
bool dfs(int p)
{
vis1[p]=true; //标记本次匹配涉及多少男生尝试进行换女生
for(int i=1;i<=m;i++)
if(!vis2[i]) //保证每次寻找增广路在V集中的点只访问一次
{
if(val1[p]+val2[i]==favor[p][i]) //男生与女生存在着连线(即这两人可以进行匹配)
{
vis2[i]=true;
if(!match[i]||dfs(match[i])) //匈牙利算法,寻找增广路
{
match[i]=p;
return true;
}
}
else
slack[i]=min(slack[i],val1[p]+val2[i]-favor[p][i]); //否则将男生与女生匹配还需要的期望值取小存入slack中
}
return false;
}
ll KM()
{
for(int i=1;i<=n;i++)
{
val1[i]=-INF;
for(int j=1;j<=m;j++)
val1[i]=max(val1[i],favor[i][j]); //初始val1的值为与其相邻边权的最大值
}
for(int i=1;i<=m;i++)
{
match[i]=0; //注意match数组记录的是第i个女生匹配到的男生编号
val2[i]=0;
}
for(int i=1;i<=n;i++)
{
memset(slack,INF,sizeof slack);
while(true) //只要没找到匹配,就降低期望值一直找下去
{
memset(vis1,false,sizeof vis1);
memset(vis2,false,sizeof vis2);
if(dfs(i))
break; //如果能找到匹配就退出
ll d=INF; //找不到就减少期望值继续找
for(int j=1;j<=m;j++)
if(!vis2[j])
d=min(d,slack[j]); //在所有未访问过的女生匹配所需期望值再取小(最大程度减少换人匹配的期望损耗)
for(int j=1;j<=n;j++)
if(vis1[j])
val1[j]-=d; //如果是上一趟匹配访问过的男生,就降低他的期望值
for(int j=1;j<=m;j++)
if(vis2[j])
val2[j]+=d; //如果是上一趟匹配访问过的女生,就增加她的期望值
}
}
ll res=0;
for(int i=1;i<=m;i++)
if(match[i])
res+=favor[match[i]][i];
return res;
}
int main()
{
ios::sync_with_stdio(0);
cin.tie(0);cout.tie(0);
while(cin>>n>>m)
{
int k=n+1;
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{
cin>>favor[i][j];
favor[i][j]*=k;
}
}
int sum=0,dd;
for(int i=1;i<=n;i++)
{
cin>>dd;
sum+=favor[i][dd]/k;
favor[i][dd]++;
}
int res=KM();
cout<<n-res%k<<' '<<res/k-sum<<'
';
}
return 0;
}
完整程序(BFS)
DFS理论上可以被卡到(O(n^4)),这题的数据范围完全经不起这样折腾
可以发现的是,每次寻找增广路实际上只是更改一条边
而在这条边之前尝试寻找的增广路(寻找失败的)是无效的
所以每次DFS会重新寻找那些已经已知是无效的边,耗费时间
所以换成BFS,记录下每次寻找的状态,让下一次匹配跟在上一次的状态之后
这样即可将最坏情况的时间复杂度降到(O(n^3))
两集合数量相同情况
以Luogu P6577 - 【模板】二分图最大权完美匹配为例
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int INF=0x3f3f3f3f;
const int N=55;
int n,m,match[N],pre[N];
bool vis2[N];
ll favor[N][N],val1[N],val2[N],slack[N];
void bfs(int p)
{
int x,y=0,yy=0;
memset(pre,0,sizeof pre);
memset(slack,INF,sizeof slack);
match[0]=p;
do{
ll d=INF;
x=match[y];
vis2[y]=true;
for(int i=1;i<=n;i++)
{
if(vis2[i])
continue;
if(slack[i]>val1[x]+val2[i]-favor[x][i])
{
slack[i]=val1[x]+val2[i]-favor[x][i];
pre[i]=y;
}
if(slack[i]<d)
{
d=slack[i]; //d取最小可能
yy=i; //记录最小可能存在的点
}
}
for(int i=0;i<=n;i++)
{
if(vis2[i])
val1[match[i]]-=d,val2[i]+=d;
else
slack[i]-=d;
}
y=yy;
}while(match[y]);
while(y)
{
match[y]=match[pre[y]]; //bfs对访问路径进行记录,并在最后一并改变match
y=pre[y];
}
}
ll KM()
{
memset(match,0,sizeof match);
memset(val1,0,sizeof val1);
memset(val2,0,sizeof val2);
for(int i=1;i<=n;i++)
{
memset(vis2,false,sizeof vis2);
bfs(i);
}
ll res=0;
for(int i=1;i<=n;i++)
res+=favor[match[i]][i]; //最后将对应匹配的边权求和输出
return res;
}
int main()
{
int u,v;
ll w;
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
favor[i][j]=-INF;
for(int i=1;i<=m;i++)
{
scanf("%d%d%lld",&u,&v,&w);
favor[u][v]=max(favor[u][v],w);
}
printf("%lld
",KM());
for(int i=1;i<=n;i++)
printf("%d ",match[i]);
return 0;
}
两集合数量不同情况
以HDU 2853为例,要注意每个循环是以(U)集为底还是以(V)集为底
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int INF=0x3f3f3f3f;
const int N=55;
int n,m,match[N],pre[N];
bool vis2[N];
ll favor[N][N],val1[N],val2[N],slack[N];
void bfs(int p)
{
int x,y=0,yy=0;
memset(pre,0,sizeof pre);
memset(slack,INF,sizeof slack);
match[0]=p;
do{
ll d=INF;
x=match[y];
vis2[y]=true;
for(int i=1;i<=m;i++)
{
if(vis2[i])
continue;
if(slack[i]>val1[x]+val2[i]-favor[x][i])
{
slack[i]=val1[x]+val2[i]-favor[x][i];
pre[i]=y;
}
if(slack[i]<d)
{
d=slack[i]; //d取最小可能
yy=i; //记录最小可能存在的点
}
}
for(int i=0;i<=m;i++)
{
if(vis2[i])
val1[match[i]]-=d,val2[i]+=d;
else
slack[i]-=d;
}
y=yy;
}while(match[y]);
while(y)
{
match[y]=match[pre[y]]; //bfs对访问路径进行记录,并在最后一并改变match
y=pre[y];
}
}
ll KM()
{
memset(match,0,sizeof match);
memset(val1,0,sizeof val1);
memset(val2,0,sizeof val2);
for(int i=1;i<=n;i++)
{
memset(vis2,false,sizeof vis2);
bfs(i);
}
ll res=0;
for(int i=1;i<=m;i++)
res+=favor[match[i]][i]; //最后将对应匹配的边权求和输出
return res;
}
int main()
{
ios::sync_with_stdio(0);
cin.tie(0);cout.tie(0);
while(cin>>n>>m)
{
int k=n+1;
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{
cin>>favor[i][j];
favor[i][j]*=k;
}
}
int sum=0,dd;
for(int i=1;i<=n;i++)
{
cin>>dd;
sum+=favor[i][dd]/k;
favor[i][dd]++;
}
int res=KM();
cout<<n-res%k<<' '<<res/k-sum<<'
';
}
return 0;
}
本文参考的博客/文章如下(我就是个缝合怪qwq):
Luogu P6577 题解 (Writer: George1123)
Luogu P6577 题解 (Writer: Rainy7)
cnblogs 《KM算法详解+模板》 (Writer: wenr)
CSDN 《KM算法》 (Writer: Enjoy_process)
缝合完毕,感谢阅读!
