1 折半查找法
了解二叉查找树之前,先来看看折半查找法,也叫二分查找法
在一个有序的整数数组中(假如是从小到大排序的),如果查找某个元素,返回元素的索引。
如下:
int[] arr = new int[]{1,3,4,6,8,9};
在 arr 数组中查找6这个元素,查到返回对应的索引,没有找到就返回-1
思想很简单:
1 先找到数组中间元素target与6比较
2 如果target比6大,就在数组的左边查找
3 如果target比6小,就在数组的右边查找
java实现代码如下:
private static int binarySearch(int[] data, int target) {
int l = 0;
int r = data.length - 1;
while (l <= r) {
//int mid = (l + r) / 2;
//这句代码理论上是没有问题的,但是是有bug的
//如果因为 l + r 会超过整数的最大值,就会溢出
//所以换成下面的写法,最小边界,加上差的一半,就是中间索引
//最小边界,加上差的一半,就是中间值
int mid = l + (r - l) / 2;
if (data[mid] > target) { //如果中间的值比target大,r向右移动。
r = mid - 1;
} else if (data[mid] < target) { //如果中间的值比target小,l向左移动
l = mid + 1;
} else {
return mid; //如果中间的值与target相等,就返回下标
}
}
//没有找到就返回-1
return -1;
}
测试代码如下:
public static void main(String[] args) {
int[] data = new int[]{1,3,4,6,8,9};
System.out.println(binarySearch(data, 6));
}
输出
3
折半查找的关键是数组必须有序,一次过滤掉一半的数据,时间复杂度为O(logN)。
上面是以2为底的,N为数组的元素个数.
折半查找和下面的要讲的二分搜索树是有一样的思想
2 二分搜索树定义
二分搜索树定义双叫二分查找树,其定义如下
1 若它的左子树不为空,则左子树上所有的节点的值均小于根结点的值
2 若它的右子树不为空,则右子树上所有的节点的值均大于根结点的值
3 它的左右子树也分别为二分搜索树
由二叉搜索树的定义可知,它前提是二叉树,并且采用了递归的定义方式
。再得,它的节点满足一定的关系,左子树的节点一定比父节点的小,
右子树的节点一定比父节点的大。
构造一棵二叉搜索树的目的,其实目的不是为了排序,是为了提高查找,删除,插入关键字的速度。
下面我们用图和代码来解释二叉树的查找,插入,和删除。比如下图就是一个二叉搜索树
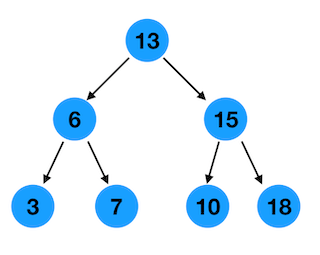
2.0 二叉搜索树的定义和节点的定义
二叉搜索树中存放的都是key。先看下二叉树的定义
//key必须继承Comparable,可以比较大小的
public class QBST<K extends Comparable<K>, V> {
...
}
二叉树中节点的定义
//QNode是作为QBST的内部类的。后面会有完整的源码
class QNode {
//key,也相当于上图中的数字,只不过不一定是数字
//只要能比较大小就行了。这里的key,是继承Comparable的
K key;
//节点中的value
V value;
//左子树
QNode left;
//右子树
QNode right;
//根据key,value构造一个节点
QNode(K key, V value) {
this.key = key;
this.value = value;
this.left = null;
this.right = null;
}
//根据一个节点,构造另一个新节点
QNode(QNode node){
this.key = node.key;
this.value = node.value;
this.left = node.left;
this.right = node.right;
}
}
类的定义和类中节点的定义都有了。
二分搜索树的定义如下:
/**
* 二分搜索树,也叫二分查找树
*/
public class QBST<K extends Comparable<K>, V> {
class QNode {
K key;
V value;
QNode left;
QNode right;
QNode(K key, V value) {
this.key = key;
this.value = value;
this.left = null;
this.right = null;
}
QNode(QNode node){
this.key = node.key;
this.value = node.value;
this.left = node.left;
this.right = node.right;
}
}
//树的根
private QNode root;
//树中节点的个数
private int count;
//构造一棵空的二分搜索树
public QBST() {
root = null;
count = 0;
}
//返回二分搜索树中的个数
public int size() {
return count;
}
//树是否为空
public boolean isEmpty() {
return count == 0;
}
}
2.1 二叉搜索树的插入
1 如果这棵树为空,新建一个节点,作为根
2 如果要插入的key比根节点大,就插入到右子树中
3 如果要插入的key比根节点小,就插入到左子树中
4 如果要插入的key和根节点相等,就更新当前节点的value
代码如下:
public void insert(K key, V value) {
root = insert(root, key, value);
}
// 向以node为根的二叉搜索树中,插入节点(key,value)
// 返回插入新节点后的二叉搜索树的根
private QNode insert(QNode node, K key, V value) {
//查检条件
checkNotNull(key,"key is null");
//如果node为空,直接new一个节点返回
if (node == null) {
count++;
return new QNode(key, value);
}
//如果key比根节点大,插入到node的右子树中
if (key.compareTo(node.key) == 1) {
node.right = insert(node.right, key, value);
//如果key比根节点小,插入到node的左子树中
} else if (key.compareTo(node.key) == -1) {
node.left = insert(node.left, key, value);
//如果key和根节点相等,更新根节点的value
} else {
node.value = value;
}
//返回根
return node;
}
2.2 二叉搜索树的查找
和上面向一棵二叉搜索树插入一个节点一样。
向一棵二叉搜索树中查找一个节点也是类似
1 如果根节点为空,不用查找了,返回null
2 如果key比根节点的key要大,在右子树中查找
3 如果key比根节点的key要小,在左子树中查找
4 如果key和根节点的key相等,返回根节点
代码实现如下:
//搜索key结果的value
public V search(K key){
return search(root,key);
}
// 向以node为根的二叉搜索树中,以key为键,返回V
private V search(QNode node,K key){
checkNotNull(key,"key is null");
//如果当前节点为null,返回null
if(node == null){
return null;
}
//如果key比根节点的key大,在右子树中查找
if(key.compareTo(node.key) == 1){
return search(node.right,key);
//如果key比根节点的key小,在左子树中查找
}else if(key.compareTo(node.key) == -1){
return search(node.left,key);
//如果key与根节点的key值相等,就返回节点的value值
}else {
return node.value;
}
}
2.3 二叉搜索树的遍历
二叉树的遍历有前序遍历,中序遍历,后序遍历,层序遍历(也叫做广度优先遍历)
如下图的二叉搜索树。

根据根节点的访问顺序,可以把遍历分为前序遍历,中序遍历,后序遍历
前序遍历:先访问根节点,再前序遍历左右子树
中序遍历:先中序遍历左子树,再访问根节点,后中序遍历右子树
后序遍历:先后序遍历左子树,再后序遍历右子树,再访问根节点
代码实现分别如下:
// 前序遍历 O(n)
public void preOrder(){
//后序遍历以root为根的二叉搜索树
preOrder(root);
}
private void preOrder(QNode node){
if(node != null){
//先遍历根节点
System.out.println(node.key);//这里的访问只是打印
//前序遍历左子树
preOrder(node.left);
//后序遍历右子树
preOrder(node.right);
}
}
// 中序遍历 O(n)
public void middleOrder(){
middleOrder(root);
}
private void middleOrder(QNode node){
if(node != null){
middleOrder(node.left);
System.out.println(node.key);
middleOrder(node.right);
}
}
// 后序遍历 O(n)
public void postOrder(){
postOrder(root);
}
private void postOrder(QNode node){
if(node != null){
postOrder(node.left);
postOrder(node.right);
System.out.println(node.key);
}
}
其中层序遍历就是一层一层的从左到右遍历
上图中层序遍历的结果是 13 6 15 3 7 10 18
代码实现需要借助队列,代码实现如下:
// 层序遍历,也叫做广度优先遍历
public void levelOrder(){
if(root == null){
return;
}
LinkedList<QNode> queue = new LinkedList<>();
queue.addLast(root);
while (!queue.isEmpty()){
QNode node = queue.removeLast();
//这里我们只打印
System.out.println(node.key);
queue.addLast(node.left);
queue.addLast(node.right);
}
}
2.4 二叉搜索树的删除
二叉搜索树最麻烦的就是删除节点,删除任意二叉树中的节点之前,我们来先删除特殊的节点。
- 删除二叉搜索树中最小的节点
- 删除二叉搜索树中最大的节点
- 查找二叉搜索树中最小的节点
- 查找二叉搜索树中最大的节点
我们先来实现这些操作。
如下图
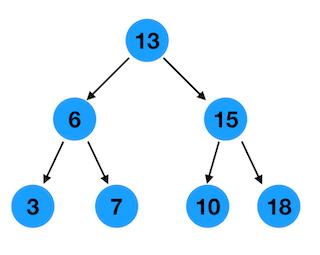
根据二叉搜索树的定义,可以得出以下结论
- 在一个二叉搜索树中,最小的节点一定是最左边的节点,也就是图中的节点 3
- 在一个二叉搜索树中,最大的节点一定是最右边的节点,也就是图中的节点 18
总之:
最小节点去左子树中找,直到节点的左孩子为空,则当前节点就是最小节点
最大节点去右子树中找,直到节点的右孩子为空,则当前节点就是最大节点
1 先来实现查找二叉搜索树中最小的节点
如下代码
//查找一棵树中最小的节点,返回 K
public K minimum(){
checkNotNull(root,"the tree is empty");
//在以根为root的二叉搜索树中返回最小节点的键值
QNode minNode = minimum(root);
//返回最小节点的键值
return minNode.key;
}
// 在以node为根的二叉搜索树中,返回最小键值的节点
private QNode minimum(QNode node){
//如果node.left == null,说明当前node节点就是最小的节点
//返回当前节点node
if(node.left == null){
return node;
}
//如果当前节点不是最小的节点
//继承往左子树中查找
return minimum(node.left);
}
同理,查找最大节点也是一样
2 实现查找二叉搜索树中最大的节点
代码如下:
public K maximum(){
checkNotNull(root,"the tree is empty");
QNode maxNode = maximum(root);
return maxNode.key;
}
// 在以node为根的二叉搜索树中,返回最大键值的节点
private QNode maximum(QNode node){
if(node.right == null){
return node;
}
return maximum(node.right);
}
上面实现了查找最小节点和最大节点,下面我们再来实现删除最小节点和删除最大节点
3 实现删除二叉搜索树中最小的节点
一直往左孩子中删除,当某一个节点node没有左孩子时,说明当前节点就是最小节点
这时候分两种情况
- 当前节点有右孩子
如果是这种情况,直接把右孩子返回,作为当前节点 - 当前节点没有右孩子
如果是这种情况,直接返回null。此时返回右孩子也行,因为右孩子也是null
代码实现如下
// 删除二叉搜索树中最小的节点
public void removeMin(){
if(root != null){
root = removeMin(root);
}
}
// 删除掉以node为根的二分搜索树中的最小的节点
// 返回删除节点后新的二分搜索树的根
private QNode removeMin(QNode node){
//如果当前当前没有左孩子,则当前节点就是最小节点
if(node.left == null){
//保存当前节点的右孩子,这句代码把上面两种情况都包含了
QNode rightNode = node.right;
node = null; //释放当前节点
count--; //记得数量要减1
return rightNode;//返回右孩子,有可能为空或者不为空
}
//递归调用删除以当前节点的左孩子为根的二叉搜索中最小的节点
node.left = removeMin(node.left);
//别忘了返回当前节点
return node;
}
同理,删除二叉搜索树中最大的节点的代码如下:
// 删除二叉搜索树中最大的节点
public void removeMax(){
if(root != null){
root = removeMax(root);
}
}
// 删除掉以node为根的二分搜索树中的最大的节点
// 返回删除节点后新的二分搜索树的根
private QNode removeMax(QNode node){
if(node.right == null){
QNode leftNode = node.left;
count--;
node = null;
return leftNode;
}
node.right = removeMax(node.right);
return node;
}
下面来分析一下删除任意一个节点。
删除任意一个节点node,那么可以分为以下几种情况
- node 没有孩子
- node 只有一个孩子
- node 有两个孩子
如下图一棵二叉搜索树,我们来分析
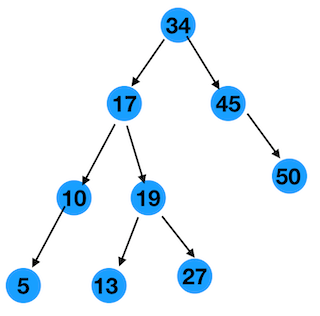
第一种情况:node没有孩子
这种情况最简单,直接删除就行了,剩下的还是一棵二叉搜索树
比如图中的 节点5,节点13,节点27,节点50,删除任意一个节点之后
剩下的还是满足一棵二叉搜索树
第二种情况:node只有一个孩子
这种情况又分两种
- node节点有一个左孩子
- node节点有一个右孩子
上面两种情况其实不影响,比如图中的节点10,节点45,分别有一个左孩子和一个右孩子。
也好办,节点10删除后,它的左孩子节点5,放在节点10的位置
同理知,节点45删除后,它的右孩子节点50,放在节点45的位置
这样一来,剩下的节点还是一棵二叉搜索树
第三种情况:node有两个孩子
还是上图为准,以节点17为例,节点17有左右两个孩子,分别是10,19
要删除节点17,怎么办呢?
或者说节点17删除 后,哪个节点应该放在节点17的位置上呢?
我们节点17满足两个性质 :
- 17大于它的左孩子10
- 17小于它的右孩子19
那么我们找到一个这样的节点,只要满足上面这两条性质,不就是可以了吗。
so easey
我们就来先找一个大于10而且小于19的节点
- 大于 10 的节点,只要在 17 的右子树
也就是以 19 为根节点的树中找不就行了吗
因为17的右子树中所有的节点都比 17 大 - 小于 19 的节点,只要在以 19 为根的树中找左孩子不就得了吗
经过上面的分析,这样的节点就是 13 啊,将17删除 ,把13放到17的位置 ,如图
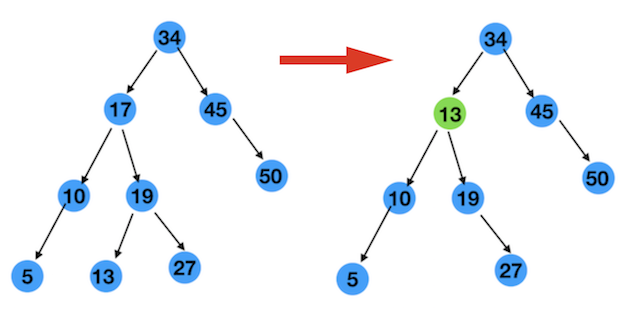
其实,把10放到17的位置也是可以的。如下图
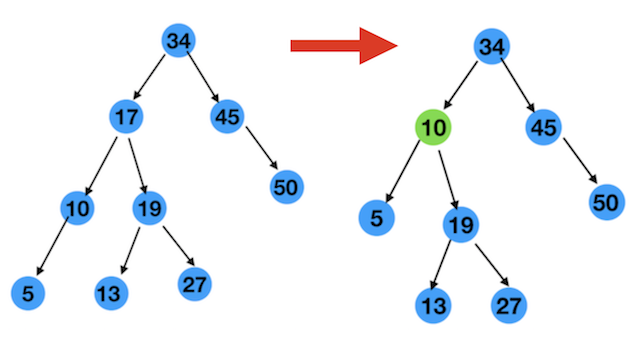
10和13两个节点都满足条件,所以我们可以得出结论
删除一个有两个孩子节点,可以找这个节点左子树中的最大节点,或者右子树中的最小节点来放到当前位置
伪代码:
删除左右都 有孩子的节点 d
找到 s = min(d.right)
s 可以叫作 d 的后继
s.right = deledeMin(d->right)
s.left = d.left;
删除 d, s 是新的子树的根
翻译成代码如下:
public void remove(K key) {
root = remove(root, key);
}
// 删除掉以node为根的二分搜索树中键值为key的节点
// 返回删除节点后新的二分搜索树的根
// O(logN)
private QNode remove(QNode node, K key) {
//如果树为null,返回null
if (node == null) {
return null;
}
//想要删除某个节点,必须先要找到这个节点
//所以下面的代码包含了查找
if (key.compareTo(node.key) == -1) {//如果key小于根节点的key
//到node的左子树查找并删除键值为key的节点
node.left = remove(node.left, key);
//返回删除节点后新的二分搜索树的根
return node;
} else if (key.compareTo(node.key) == 1) {//如果key大于根节点的key
//到node的右子树查找并删除键值为key的节点
node.right = remove(node.right, key);
//返回删除节点后新的二分搜索树的根
return node;
} else { //key == node.key,也就是找到了这个节点
//当前节点的左孩子为null
if (node.left == null) {
//保存右孩子节点
QNode rightNode = node.right;
//个数减1
count--;
//删除
node = null;
//右节点作为新的根
return rightNode;
}
//当前节点的右孩子为null
if (node.right == null) {
//保存左孩子的节点
QNode leftNode = node.left;
//个数减1
count--;
//删除
node = null;
//左节点作为新的根
return leftNode;
}
//上面的情况也包括了左右两个孩子都是null
//这样的情况就走第一种,node.left==null的条件中。也满足
//下面是 node.left != null && node.right != null的情况
//找到右子树中最小节点
QNode min = minimum(node.right);
//用最小节点新建一个节点,因为等会要删除最小的节点,所以这里我们要新建一个最小节点
QNode s = new QNode(min);
//s的右孩子,就是删除node右子树中最小节点返回的根
s.right = removeMin(node.right);
//s的左孩子,就是删除节点的左孩子
s.left = node.left;
//返回新的根
return s;
}
}
同过上面的分析,我们了解了二叉搜索树的性质,以及插入,查找,查找最大节点,查找最小节点,删除最大节点,删除最小节点,以及最后分析出来删除一个任意节点。
下面我们粘出完整代码 。如下
/**
* 二分搜索树,也叫二分查找树
*/
public class QBST<K extends Comparable<K>, V> {
class QNode {
K key;
V value;
QNode left;
QNode right;
QNode(K key, V value) {
this.key = key;
this.value = value;
this.left = null;
this.right = null;
}
QNode(QNode node) {
this.key = node.key;
this.value = node.value;
this.left = node.left;
this.right = node.right;
}
}
private QNode root;
private int count;
public QBST() {
root = null;
count = 0;
}
public int size() {
return count;
}
public boolean isEmpty() {
return count == 0;
}
public void insert(K key, V value) {
root = insert(root, key, value);
}
// 向以node为根的二叉搜索树中,插入节点(key,value)
// 返回插入新节点后的二叉搜索树的根
private QNode insert(QNode node, K key, V value) {
checkNotNull(key, "key is null");
if (node == null) {
count++;
return new QNode(key, value);
}
if (key.compareTo(node.key) == 1) {
node.right = insert(node.right, key, value);
} else if (key.compareTo(node.key) == -1) {
node.left = insert(node.left, key, value);
} else {
node.value = value;
}
return node;
}
public boolean contain(K key) {
return contain(root, key);
}
// 向以node为根的二叉搜索树中,查找是否包含key的节点
private boolean contain(QNode node, K key) {
checkNotNull(key, "key is null");
if (node == null) {
return false;
}
if (key.compareTo(node.key) == 1) {
return contain(node.right, key);
} else if (key.compareTo(node.key) == -1) {
return contain(node.left.key);
} else {
return true;
}
}
public V search(K key) {
return search(root, key);
}
// 向以node为根的二叉搜索树中,
private V search(QNode node, K key) {
checkNotNull(key, "key is null");
if (node == null) {
return null;
}
if (key.compareTo(node.key) == 1) {
return search(node.right, key);
} else if (key.compareTo(node.key) == -1) {
return search(node.left, key);
} else {
return node.value;
}
}
// 前序遍历 O(n)
public void preOrder() {
preOrder(root);
}
private void preOrder(QNode node) {
if (node != null) {
System.out.println(node.key);
preOrder(node.left);
preOrder(node.right);
}
}
// 中序遍历 O(n)
public void middleOrder() {
middleOrder(root);
}
private void middleOrder(QNode node) {
if (node != null) {
middleOrder(node.left);
System.out.println(node.key);
middleOrder(node.right);
}
}
// 后序遍历 O(n)
public void postOrder() {
postOrder(root);
}
private void postOrder(QNode node) {
if (node != null) {
postOrder(node.left);
postOrder(node.right);
System.out.println(node.key);
}
}
// 层序遍历,也叫做广度优先遍历
public void levelOrder() {
if (root == null) {
return;
}
LinkedList<QNode> queue = new LinkedList<>();
queue.addLast(root);
while (!queue.isEmpty()) {
QNode node = queue.removeLast();
System.out.println(node.key);
queue.addLast(node.left);
queue.addLast(node.right);
}
}
public void destroy() {
destroy(root);
}
// 销毁操作就是后序遍历的一次应用
private void destroy(QNode node) {
if (node != null) {
destroy(node.left);
destroy(node.right);
node = null;
count--;
}
}
public K minimum() {
checkNotNull(root, "the tree is empty");
QNode minNode = minimum(root);
return minNode.key;
}
// 在以node为根的二叉搜索树中,返回最小键值的节点
private QNode minimum(QNode node) {
if (node.left == null) {
return node;
}
return minimum(node.left);
}
public K maximum() {
checkNotNull(root, "the tree is empty");
QNode maxNode = maximum(root);
return maxNode.key;
}
// 在以node为根的二叉搜索树中,返回最大键值的节点
private QNode maximum(QNode node) {
if (node.right == null) {
return node;
}
return maximum(node.right);
}
// 删除二叉搜索树中最小的节点
public void removeMin() {
if (root != null) {
root = removeMin(root);
}
}
// 删除掉以node为根的二分搜索树中的最小的节点
// 返回删除节点后新的二分搜索树的根
private QNode removeMin(QNode node) {
if (node.left == null) {
QNode rightNode = node.right;
node = null;
count--;
return rightNode;
}
node.left = removeMin(node.left);
return node;
}
// 删除二叉搜索树中最大的节点
public void removeMax() {
if (root != null) {
root = removeMax(root);
}
}
// 删除掉以node为根的二分搜索树中的最大的节点
// 返回删除节点后新的二分搜索树的根
private QNode removeMax(QNode node) {
if (node.right == null) {
QNode leftNode = node.left;
count--;
node = null;
return leftNode;
}
node.right = removeMax(node.right);
return node;
}
public void remove(K key) {
root = remove(root, key);
}
// 删除掉以node为根的二分搜索树中键值为key的节点
// 返回删除节点后新的二分搜索树的根
// O(logN)
private QNode remove(QNode node, K key) {
//如果树为null,返回null
if (node == null) {
return null;
}
//想要删除某个节点,必须先要找到这个节点
//所以下面的代码包含了查找
if (key.compareTo(node.key) == -1) {//如果key小于根节点的key
//到node的左子树查找并删除键值为key的节点
node.left = remove(node.left, key);
//返回删除节点后新的二分搜索树的根
return node;
} else if (key.compareTo(node.key) == 1) {//如果key大于根节点的key
//到node的右子树查找并删除键值为key的节点
node.right = remove(node.right, key);
//返回删除节点后新的二分搜索树的根
return node;
} else { //key == node.key,也就是找到了这个节点
//当前节点的左孩子为null
if (node.left == null) {
//保存右孩子节点
QNode rightNode = node.right;
//个数减1
count--;
//删除
node = null;
//右节点作为新的根
return rightNode;
}
//当前节点的右孩子为null
if (node.right == null) {
//保存左孩子的节点
QNode leftNode = node.left;
//个数减1
count--;
//删除
node = null;
//左节点作为新的根
return leftNode;
}
//上面的情况也包括了左右两个孩子都是null
//这样的情况就走第一种,node.left==null的条件中。也满足
//下面是 node.left != null && node.right != null的情况
//找到右子树中最小节点
QNode min = minimum(node.right);
//用最小节点新建一个节点,因为等会要删除最小的节点,所以这里我们要新建一个最小节点
QNode s = new QNode(min);
//s的右孩子,就是删除node右子树中最小节点返回的根
s.right = removeMin(node.right);
//s的左孩子,就是删除节点的左孩子
s.left = node.left;
//返回新的根
return s;
}
}
private <E> void checkNotNull(E e, String message) {
if (e == null) {
throw new IllegalArgumentException(message);
}
}
}
欢迎访问作者的helloworld的个人博客:
https://www.helloworld.net/jiulu
同时也可以加作者的微信:daitukeji
也可以扫下面的二维码添加
