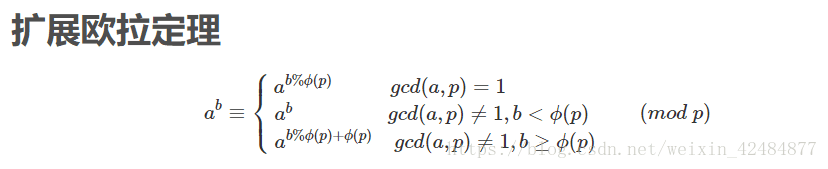【BZOJ5394】【Ynoi2016】—炸脖龙（树状数组+广义欧拉定理）

传送门

---

考虑广义欧拉定理

直接暴力从左到右扫
这样最多$log$次模数就变成1了
然后就没了
注意快速幂的时候记一下取没取模
每层不要乱取模，因为每次模数不一样

复杂度$O(nlog^2n+p)$
有点小卡空间

#include<bits/stdc++.h>
using namespace std;
const int RLEN=1<<21|1;
#define ll long long
inline char gc(){
	static char ibuf[RLEN],*ib,*ob;
	(ob==ib)&&(ob=(ib=ibuf)+fread(ibuf,1,RLEN,stdin));
	return (ib==ob)?EOF:*ib++;
}
inline int read(){
	char ch=gc();int res=0,f=1;
	while(!isdigit(ch))f^=ch=='-',ch=gc();
	while(isdigit(ch))res=(res+(res<<2)<<1)+(ch^48),ch=gc();
	return f?res:-res;
}
const int N=500005;
const int M=20000007;
int phi[M],pr[M],n,m,tot,vis[M],a[N];
ll tr[N];
#define lowbit(x) (x&(-x))
inline void update(int p,ll k){
	for(;p<=n;p+=lowbit(p))tr[p]+=k;
}
inline ll query(int p,ll res=0){
	for(;p;p-=lowbit(p))res+=tr[p];return res;
}
inline void init(){
	for(int i=2;i<=M-7;i++){
		if(!vis[i]){pr[++tot]=i,phi[i]=i-1;}
		for(int j=1;j<=tot&&1ll*pr[j]*i<=M-7;j++){
			vis[i*pr[j]]=1;
			if(i%pr[j]==0){phi[i*pr[j]]=phi[i]*pr[j];break;}
			phi[i*pr[j]]=phi[i]*(pr[j]-1);
		}
	}
}
inline int ksm(ll a,ll b,int mod,ll res=1){
	int f1=0,f2=0;
	if(a>=mod)a%=mod,f2=1;
	for(;b;b>>=1,a=a*a,(a>=mod)?(a%=mod,f2=1):0){
		if(b&1){
			res=res*a,f1=f2;
			if(res>=mod)res%=mod,f1=1;
		}
	}
	res=res+f1*mod;
	return res;
}
inline ll solve(int pos,int des,ll mod){
	if(mod==1||pos>des)return 1;
	ll x=query(pos)+a[pos],y=solve(pos+1,des,phi[mod]);
	return ksm(x,y,mod);
}
int main(){
	init();n=read(),m=read();
	for(int i=1;i<=n;i++)a[i]=read();
	for(int i=1;i<=m;i++){
		int op=read(),l=read(),r=read(),k=read();
		if(op==1){
			update(l,k),update(r+1,-k);
		}
		else{
			cout<<solve(l,r,k)%k<<'
';
		}
	}
}