可持续化权值线段树(主席树)各种变体
简单介绍
博客安利: https://oi-wiki.org/ds/persistent-seg/ , https://blog.csdn.net/bestFy/article/details/78650360
主席树其实是多颗线段树的效果+前缀和的思想,只不过在空间上有了很大的优化,具体优化思路在于每次更新(每次修改对应一颗新的线段树)只会改变二叉树某一条链上的节点,新的线段树可以继承前一颗线段树的没有改变的节点,只为有了更新的节点新建一个节点。
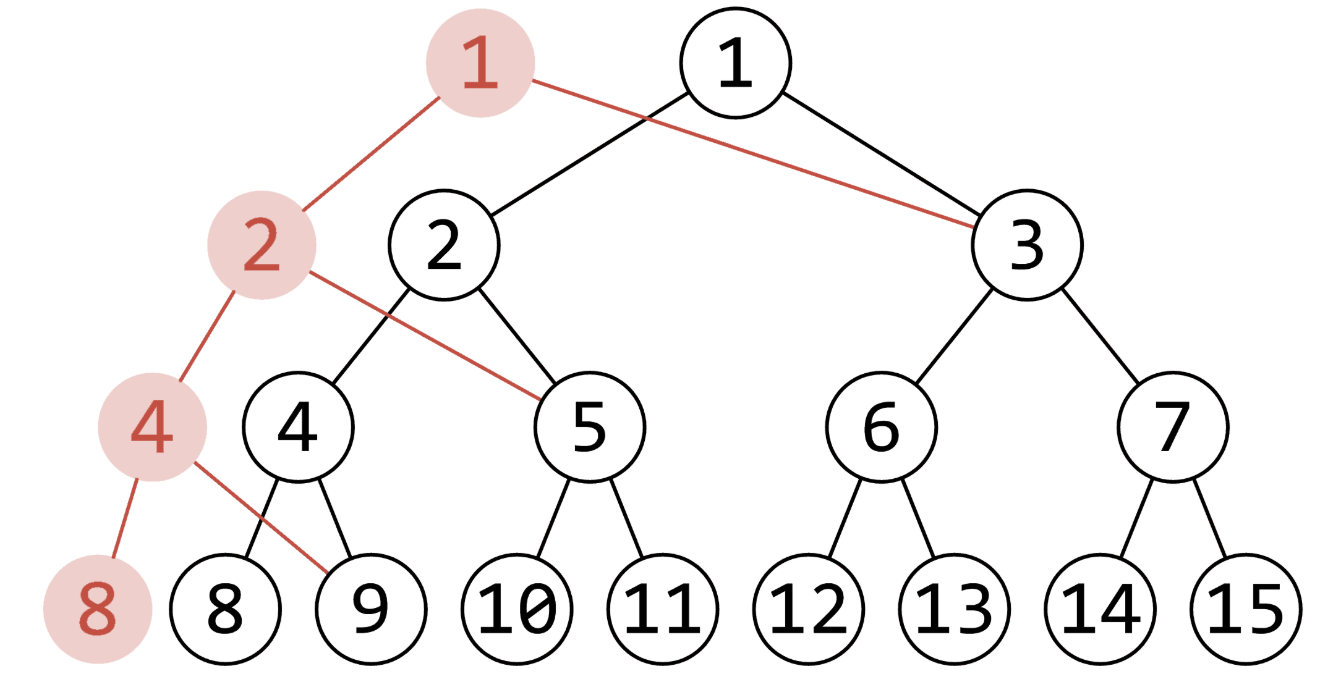
关于空间问题:由于是动态开点,一颗线段树最会出现2*n-1个结点,n次修改,每次最多影响一条链(log n个结点),最坏情况为2*n-1+nlog n,对于1e5的数据,这个值大概是19e5,oi.wiki上表示过于吝啬空间可能会被莫名其妙的卡掉,最好使用(n<<5),空间紧张的情况下至少开20倍空间。
静态区间第k小
#include <bits/stdc++.h>
using namespace std;
#define fre freopen("data.in","r",stdin);
#define frew freopen("sol.out","w",stdout);
#define ms(a) memset((a),0,sizeof(a))
#define rep(i, a, b) for(register int i=(a);(i)<(b);++(i))
#define rev(i, a, b) for(register int i=(a);(i)>(b);--(i))
#define erep(i, a, b) for(register int i=(a);(i)<=(b);++(i))
#define erev(i, a, b) for(register int i=(a);(i)>=(b);--(i))
#define all(x) (x).begin(),(x).end()
#define bug(x) cout<<x<<endl;
#define pb push_back
#define lson l,m,i<<1
#define rson m+1,r,i<<1|1
#define reg register
#define pc putchar('
')
typedef long long LL;
const int inf = (0x7f7f7f7f);
inline void sf(int &x) {
x = 0;
int w = 0;
char ch = 0;
while (!isdigit(ch)) {
w |= ch == '-';
ch = getchar();
}
while (isdigit(ch)) x = (x << 3) + (x << 1) + (ch ^ 48), ch = getchar();
x = (w ? -x : x);
}
inline void pf(int x) {
if (x < 0) putchar('-'), x = -x;
if (x > 9) pf(x / 10);
putchar(x % 10 + '0');
}
const int maxn =1e5 + 5;
int n,m,len;
int a[maxn],d[maxn];
//l,r记录该节点左右子树的根节点的下标编号,v记录该区间的值
struct node{int l,r,v;}t[maxn*22];
//T[i]记录第i颗线段树的根节点
int T[maxn];
inline void discretize(){
sort(d+1,d+1+n);
len=unique(d+1,d+n+1)-d-1;
erep(i,1,n) {
a[i] = lower_bound(d + 1, d + 1 + len, a[i]) - d - 1 + 1;//从1开始
//cout<<a[i]<<' ';
}
}
//cnt给每一个节点一个编号,便于通过下标直接访问
int cnt=0;
int build(int l,int r){//动态建树,一颗空树
//p为节点下标编号
int p=++cnt,mid=l+r >>1;
if(l<r){
t[p].l=build(l,mid);
t[p].r=build(mid+1,r);
}
t[p].v=0;
return p;
}
int update(int pre,int l,int r,int& x){
int p=++cnt,mid= l+r>>1;
//继承前一颗线段树的左右子树
t[p].l=t[pre].l,t[p].r=t[pre].r,t[p].v=t[pre].v+1;
if(l<r){
//根据更新点的位置决定修改左子树还是右子树
if(x<=mid)t[p].l=update(t[pre].l,l,mid,x);
else t[p].r=update(t[pre].r,mid+1,r,x);
}
return p;
}
int query(int x,int y,int k,int l,int r){
if(l==r)return l;
//sum使用前缀和思想,得到区间线段树
int sum=t[t[y].l].v-t[t[x].l].v,mid=l+r>>1;
if(k<=sum)return query(t[x].l,t[y].l,k,l,mid);
else return query(t[x].r,t[y].r,k-sum,mid+1,r);
}
int main() {
sf(n);sf(m);
erep(i,1,n)sf(a[i]),d[i]=a[i];
discretize();
T[0]=build(1,len);//新建一颗空树
erep(i,1,n)T[i]=update(T[i-1],1,len,a[i]);//每次修改对应一颗新的线段树
while(m--){
int l,r,k;
sf(l);sf(r);sf(k);
printf("%d
",d[query(T[l-1],T[r],k,1,len)]);//记得离散回原来的数
}
return 0;
}
动态区间第k小-树状数组+主席树
这份代码是离线做法
题目链接:
长度为N的序列,M次询问:
- 查询区间第k小
- 修改某个位置的值,单点修改
使用了树状数组的二进制思想对主席树进行优化
(T[i])这颗线段树代表([i−lowbit(x)+1,x])这段区间建成的线段树:
- 修改操作,最多修改logn颗线段树即可。
- 查询操作,用不超过(2∗log2n)颗线段树就能拼(前缀和)出([l_i,r_i])的线段树。
注意,在查询时的代码实现:
用XX数组存储拼出[1,x−1]的所有点。
用YY数组存储拼出[1,y]的所有点。
然后用普通主席树的方法,让所有的跟着跳,对位相减即可。
时间复杂度(O(nlog^2n)),空间复杂度(O(2n+(n+m)log^2n))
#include <cstdio>
#include <iostream>
#include <algorithm>
using namespace std;
//P为最多可能的线段树点数
const int N = 100005, P = N * 441, L = 20;
//操作序列
struct Ops{
int i, j, k;
}op[N];
//线段树
struct SegTree{
int l, r, v;
}t[P];
//d数组为离散化数组
int n, m, len = 0, a[N], d[N << 1];
//T[i] 以 [i - lowbit(x) + 1, x] 这段区间的线段树的根节点
//X[i]、Y[i]代表多个点跟着跳,类似于普通版的$x, y$。
int T[N], tot = 0, X[L], Y[L], cx, cy;
char s[2];
int build(int l, int r){
int p = ++tot, mid = (l + r) >> 1;
t[p].v = 0;
if(l < r){
t[p].l = build(l, mid);
t[p].r = build(mid + 1, r);
}
return p;
}
int update(int pre, int l, int r, int x, int v){
int p = ++tot, mid = (l + r) >> 1;
t[p].l = t[pre].l, t[p].r = t[pre].r, t[p].v = t[pre].v + v;
if(l < r){
if(x <= mid) t[p].l = update(t[pre].l, l, mid, x, v);
else t[p].r = update(t[pre].r, mid + 1, r, x, v);
}
return p;
}
//把 [1, i] (x <= i <= n) 的线段树中值域为 a[x] 的次数 += v
void inline add(int x, int v){
int val = lower_bound(d + 1, d + 1 + len, a[x]) - d;
for(; x <= n; x += x & -x)
T[x] = update(T[x], 1, len, val, v);
}
int query(int l, int r, int k){
if(l == r) return l;
int mid = (l + r) >> 1, sum = 0;
//前缀和
for(int i = 1; i <= cx; i++)
sum -= t[t[X[i]].l].v;
for(int i = 1; i <= cy; i++)
sum += t[t[Y[i]].l].v;
if(k <= sum){
//跟着跳
for(int i = 1; i <= cx; i++)
X[i] = t[X[i]].l;
for(int i = 1; i <= cy; i++)
Y[i] = t[Y[i]].l;
return query(l, mid, k);
}else{
//跟着跳
for(int i = 1; i <= cx; i++)
X[i] = t[X[i]].r;
for(int i = 1; i <= cy; i++)
Y[i] = t[Y[i]].r;
return query(mid + 1, r, k - sum);
}
}
int main(){
scanf("%d%d", &n, &m);
for(int i = 1; i <= n; i++)
scanf("%d", a + i), d[++len] = a[i];
for(int i = 1; i <= m; i++){
scanf("%s", s);
if(s[0] == 'Q') {
scanf("%d%d%d", &op[i].i, &op[i].j, &op[i].k);
}else{
scanf("%d%d", &op[i].i, &op[i].j);
d[++len] = op[i].j; op[i].k = 0;
}
}
//离散化
sort(d + 1, d + 1 + len);
len = unique(d + 1, d + 1 + len) - (d + 1);
//这里建树,将每一个根节点初始化成1。
T[0] = build(1, len);
for(int i = 1; i <= n; i++)
T[i] = 1;
//建立可持久化线段树
for(int i = 1; i <= n; i++)
add(i, 1);
//处理询问
for(int i = 1; i <= m; i++){
if(op[i].k){
//是查询操作
cx = 0; cy = 0;
//把需要跳的点扔进去
for(int j = op[i].i - 1; j; j -= j & -j)
X[++cx] = T[j];
for(int j = op[i].j; j; j -= j & -j)
Y[++cy] = T[j];
printf("%d
", d[query(1, len, op[i].k)]);
}else{
//修改操作
add(op[i].i, -1);
a[op[i].i] = op[i].j;
add(op[i].i, 1);
}
}
return 0;
}