什么是先序、中序、后序
- 先序遍历先访问根结点,再先序遍历左子树,再先序遍历右子树
- 中序先中序遍历左子树,再访问根节点,再遍历右子树
- 后序先遍历左子树,再遍历右子树,再访问根节点
各顺序的实质(窍门)
各顺序遍历走的路径相同,从根节点从左边开始绕着二叉树走,每个结点会遇到3次,先序就是第一次遇到结点就输出一次(或者其他操作),中序就是第二次碰到时输出,后序就是第三次碰到时输出。
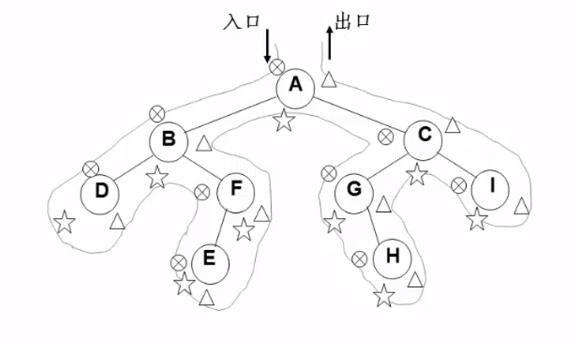
递归实现
先序遍历的递归遍历算法
void PreOrderTraversal(BinTree BT)
{
if(BT)
{
printf("%d",BT->Date);
PreOrderTraversal(BT->Left);
PreOrderTraversal(BT->Right);
}
}
中序遍历
void InOrderTraversal(Bintree BT)
{
if(BT){
InOrderTraversal(BT->Left);
printf("%d",BT->Date);
InorderTraversal(BT->Right);
}
}
后序遍历
void PostOrderTraversal(BinTree BT)
{
if(BT)
{
PreOrderTraversal(BT->Left);
PreOrderTraversal(BT->Right);
printf("%d",BT->Date);
}
}
堆栈循环实现
先序遍历的非递归循环算法
void PreOrderTraversal(BinTree BT)
{
BinTree T=BT;
Stack S=CreatStack(Maxsize);//创建并初始化堆栈
while(T || !IsEmpty(S)){
while(T){ //一直向左并将沿途结点压入堆栈
printf("%d",T->Date);//第一次遇到时就打印
push(S,T);
T=T->Left;
}
if(!IsEmpty(S)){
T=pop(S);//结点弹出堆栈
T=T->Right;//转向右结点
}
}
}
中序遍历的非递归循环算法
- 遇到一个节点把他压栈,并去遍历它的左子树
- 当左子树遍历完成,弹出栈顶节点,并访问它
- 然后根据其右指针中序遍历其右子树
void InOrdertraversal(BinTree BT)
{
BinTree T=BT;
Stack S=CreatStack(Maxsize);//创建并初始化栈
while(T || !IsEmpty(S)){
while(T){//中序遍历第二次碰到时再打印
push(S,T);
T=T->Left;
}
if(!IsEmpty(S)){
T=pop(S);
printf("%d",T->Date);
T=T->Right;
/*访问最左边的叶子结点时,打印了它本身,
再将它的右子树(NULL)赋值给T,经过判断,
就会弹出叶子结点的父元素。如果理解不了就记住。*/
}
}
}
后序遍历

从根节点开始,向左绕圈,第3次经过的节点并输出就是后序遍历。
如果逆着来看,从右边开始绕圈,第1次经过的结点刚好是从左边绕圈第3次经过的结点
只不过方向刚好相反,我们可以把前序遍历的Left与Right交换位置,然后再用另一个栈记录每次遇到的结点
最后依次取出来
void PostOrderTraversal(BinTree BT)
{
BinTree T=BT;
Stack S=CreatStack(Maxsize);//创建并初始化堆栈
Stack R=CreatStack(Maxsize);
while(T || !IsEmpty(S)){
while(T){ //一直向右并将沿途结点压入堆栈
push(R,T);
push(S,T);
T=T->Right;
}
if(!IsEmpty(S)){
T=pop(S);//结点弹出堆栈
T=T->Left;
}
}
while(!IsEmpty(R)){//R弹栈
T=pop(R);
printf("%d",T->Date);
}
}