题意描述:给你N个点和M条边,要求构造出两个(不必联通的)无向图,无重边和自环,使得独立的点(不与其他点连接的点)最少或最多。
题解:
首先考虑独立点最少的情况:对于M条边,效率最高的方法显然是让这些边没有公共点,也就是说连成由两个点和一个边组成的小单位
这样M条边可以消除最多2M个独立点。剩下的就是(N-2M)。要注意,如果(N-2M)<0,则要将答案设为0。
然后考虑独立点最多的情况:也就是说我们要考虑使每条边的利用效率最低。
等同于可以这样想:加入每个点,使这个点消耗的边最多,一直添加到没有变剩余为止。
我们可以在新的点加入时,将其连接到所有已经不是独立点的点上,这样就能最多的消耗边。
举个例子: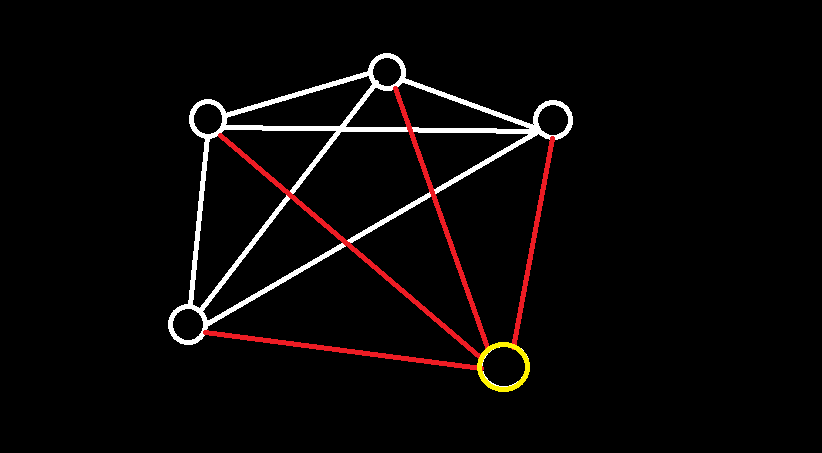
将黄色的点加入时,将其和所有已经不独立的点连一条边(红色)显然能够消耗最多的边,同时只消除一个独立点(黄色点)。
很明显,加入第 $ i $ 个点时,能够连的边有 $ i-1 $ 条。
一直这样加下去直到没有边了为止,此时剩下的点就都是独立点了。
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#define LL long long
using namespace std;
LL n,m,ans1,ans2;
int main(){
scanf("%lld%lld",&n,&m);
if(m==0){
ans1=ans2=n;
}
else{
ans1=n-(m*2);
if(ans1<0)ans1=0;
int i=1;
while(m>0){
m-=i;
i++;
}
ans2=n-i;
}
printf("%lld %lld",ans1,ans2);
return 0;
}