classification problems, Evaluation metrics:
Accuracy:
def accuracy(y_true, y_pred):
"""
Function to calculate accuracy
:param y_true: list of true values
:param y_pred: list of predicted values
:return: accuracy score
"""
# initialize a simple counter for correct predictions
correct_counter = 0
# loop over all elements of y_true
# and y_pred "together"
for yt, yp in zip(y_true, y_pred):
if yt == yp:
# if prediction is equal to truth, increase the counter
correct_counter += 1
# return accuracy
# which is correct predictions over the number of samples
return correct_counter / len(y_true)
True positive (TP): 正例 预测正确 正例预测为正例
True negative (TN): 负例 预测正确 负例预测为负例
False positive (FP): 负例 预测错误 负例预测为正例
False negative (FN):正例 预测错误 正例预测为负例
def true_positive(y_true, y_pred):
"""
Function to calculate True Positives
:param y_true: list of true values
:param y_pred: list of predicted values
:return: number of true positives
"""
# initialize
tp = 0
for yt, yp in zip(y_true, y_pred):
if yt == 1 and yp == 1:
tp += 1
return tp
def true_negative(y_true, y_pred):
"""
Function to calculate True Negatives
:param y_true: list of true values
:param y_pred: list of predicted values
:return: number of true negatives
"""
# initialize
tn = 0
for yt, yp in zip(y_true, y_pred):
if yt == 0 and yp == 0:
tn += 1
return tn
def false_positive(y_true, y_pred):
"""
Function to calculate False Positives
:param y_true: list of true values
:param y_pred: list of predicted values
:return: number of false positives
"""
# initialize
fp = 0
for yt, yp in zip(y_true, y_pred):
if yt == 0 and yp == 1:
fp += 1
return fp
def false_negative(y_true, y_pred):
"""
Function to calculate False Negatives
:param y_true: list of true values
:param y_pred: list of predicted values
:return: number of false negatives
"""
# initialize
fn = 0
for yt, yp in zip(y_true, y_pred):
if yt == 1 and yp == 0:
fn += 1
return fn
Accuracy Score = (TP + TN) / (TP + TN + FP + FN)
def accuracy_v2(y_true, y_pred):
"""
Function to calculate accuracy using tp/tn/fp/fn
:param y_true: list of true values
:param y_pred: list of predicted values
:return: accuracy score
"""
tp = true_positive(y_true, y_pred)
fp = false_positive(y_true, y_pred)
fn = false_negative(y_true, y_pred)
tn = true_negative(y_true, y_pred)
accuracy_score = (tp + tn) / (tp + tn + fp + fn)
return accuracy_score
Precision (P) :Precision = TP / (TP + FP)
def precision(y_true, y_pred):
"""
Function to calculate precision
:param y_true: list of true values
:param y_pred: list of predicted values
:return: precision score
"""
tp = true_positive(y_true, y_pred)
fp = false_positive(y_true, y_pred)
precision = tp / (tp + fp)
return precision
Recall (R) :Recall = TP / (TP + FN)
def recall(y_true, y_pred):
"""
Function to calculate recall
:param y_true: list of true values
:param y_pred: list of predicted values
:return: recall score
"""
tp = true_positive(y_true, y_pred)
fn = false_negative(y_true, y_pred)
recall = tp / (tp + fn)
return recall
F1 score (F1):F1 = 2PR / (P + R)
def f1(y_true, y_pred):
"""
Function to calculate f1 score
:param y_true: list of true values
:param y_pred: list of predicted values
:return: f1 score
"""
p = precision(y_true, y_pred)
r = recall(y_true, y_pred)
score = 2 * p * r / (p + r)
return score
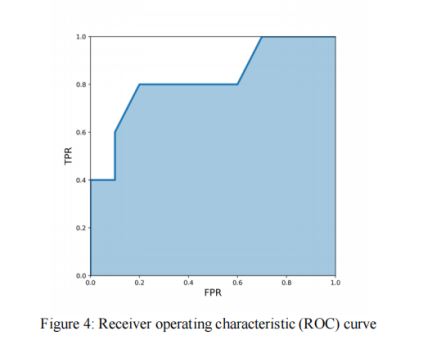
Area under the ROC (Receiver Operating Characteristic) curve or simply AUC (AUC)
AUC values range from 0 to 1,
TPR = TP / (TP + FN)
Even though it is same as recall, we will make a python function for it for further use with this name.
def tpr(y_true, y_pred):
"""
Function to calculate tpr
:param y_true: list of true values
:param y_pred: list of predicted values
:return: tpr/recall
"""
return recall(y_true, y_pred)
And FPR or False Positive Rate, which is defined as:FPR = FP / (TN + FP)
def fpr(y_true, y_pred):
"""
Function to calculate fpr
:param y_true: list of true values
:param y_pred: list of predicted values
:return: fpr
"""
fp = false_positive(y_true, y_pred)
tn = true_negative(y_true, y_pred)
return fp / (tn + fp)
FPR is known as specificity or True Negative Rate or TNR.
Log loss
Precision at k (P@k)
Average precision at k (AP@k)
Mean average precision at k (MAP@k)
regression problems, Evaluation metrics:
Mean absolute error (MAE)
import numpy as np
def mean_absolute_error(y_true,y_pred):
"""
this function calculates mae
:param y_true: list of real numbers,true values
:param y_pred: list of real numbers,predicted values
:return: mean absolute error
"""
error = 0
for yt, yp in zip(y_true,y_pred):
error = np.abs(yt - yp)
return error / len(y_true)
Mean squared error (MSE)
# squared error and mean squared error (MSE)
# Squared Error = ( True Value – Predicted Value )2
import numpy as np
def mean_squared_error(y_true,y_pred):
"""
This function calculates mse
:param y_true: list of real numbers,true values
:param y_pred: list of real numvers,predicted values
:return: mean squared error
"""
error = 0
for yt, yp in zip(y_true, y_pred):
error += (yt - yp) ** 2
return error / len(y_true)
Root mean squared error (RMSE)
# RMSE (root mean squared error)
# RMSE = SQRT ( MSE )
import numpy as np
def root_mean_squared_error(y_true,y_pred):
"""
This function calculates rmse
:param y_true: list of real numbers,true values
:param y_pred: list of real numvers,predicted values
:return: root mean squared error
"""
error = 0
for yt, yp in zip(y_true, y_pred):
error += (yt - yp) ** 2
return np.sqrt(error / len(y_true))
Root mean squared logarithmic error (RMSLE)
# MSLE (mean squared logarithmic error)
import numpy as np
def mean_squared_log_error(y_true,y_pred):
"""
This function calculates msle
:param y_true: list of real numbers, true_values
:param y_pred: list of real numbers, predicted values
:return: mean squared logarithmic error
"""
error = 0
for yt, yp in zip(y_true, y_pred):
error += (np.log(1 + yt) - np.log(1 + yp)) ** 2
return error / len(y_true)
# Root mean squared logarithmic error
import numpy as np
def root_mean_squared_log_error(y_true,y_pred):
"""
This function calculates msle
:param y_true: list of real numbers, true_values
:param y_pred: list of real numbers, predicted values
:return: mean squared logarithmic error
"""
error = 0
for yt, yp in zip(y_true, y_pred):
error += (np.log(1 + yt) - np.log(1 + yp)) ** 2
return np.sqrt(error / len(y_true))
Mean percentage error (MPE)
# the percentage error:
# Percentage Error = ( ( True Value – Predicted Value ) / True Value ) * 100
def mean_percentage_error(y_true, y_pred):
"""
This function calculates mpe
:param y_true: list of real numbers, true values
:param y_pred: list of real numbers, predicted values
:return: mean percentage error
"""
error = 0
for yt, yp in zip(y_true, y_pred):
error += (yt - yp) / yt
return error / len(y_true)
Mean absolute percentage error (MAPE)
# mean absolute percentage error or MAPE
import numpy as np
def mean_abs_percentage_error(y_true, y_pred):
"""
This function calculates MAPE
:param y_true: list of real number, true values
:param y_pred: list of real number, predicted values
:return: mean absolute percentage error
"""
error = 0
for yt, yp in zip(y_true, y_pred):
error += np.abs(yt - yp) / yt
return error / len(y_true)
R2
# R2 (R-squared), also known as the coefficient of determination.
import numpy as np
def r2(y_true, y_pred):
"""
This function calculates r-squared score
:param y_true: list of real numbers, true values
:param y_pred: list of real numbers, predicted values
:return: r2 score
"""
# calculate the mean value of true values
mean_true_value = np.mean(y_true)
# initialize numerator with 0
numerator = 0
# initialize denominator with 0
denominator = 0
# loop over all true and predicted values
for yt, yp in zip(y_true, y_pred):
# update numerator
numerator += (yt - yp) ** 2
# update denominator
denominator += (yt - mean_true_value) ** 2
# calculate the ratio
ratio = numerator / denominator
# return 1 - ratio
return 1 - ratio