一、状态和模型
在CNN网络中的训练样本的数据为IID数据(独立同分布数据),所解决的问题也是分类问题或者回归问题或者是特征表达问题。但更多的数据是不满足IID的,如语言翻译,自动文本生成。它们是一个序列问题,包括时间序列和空间序列。这时就要用到RNN网络,RNN的结构图如下所示:
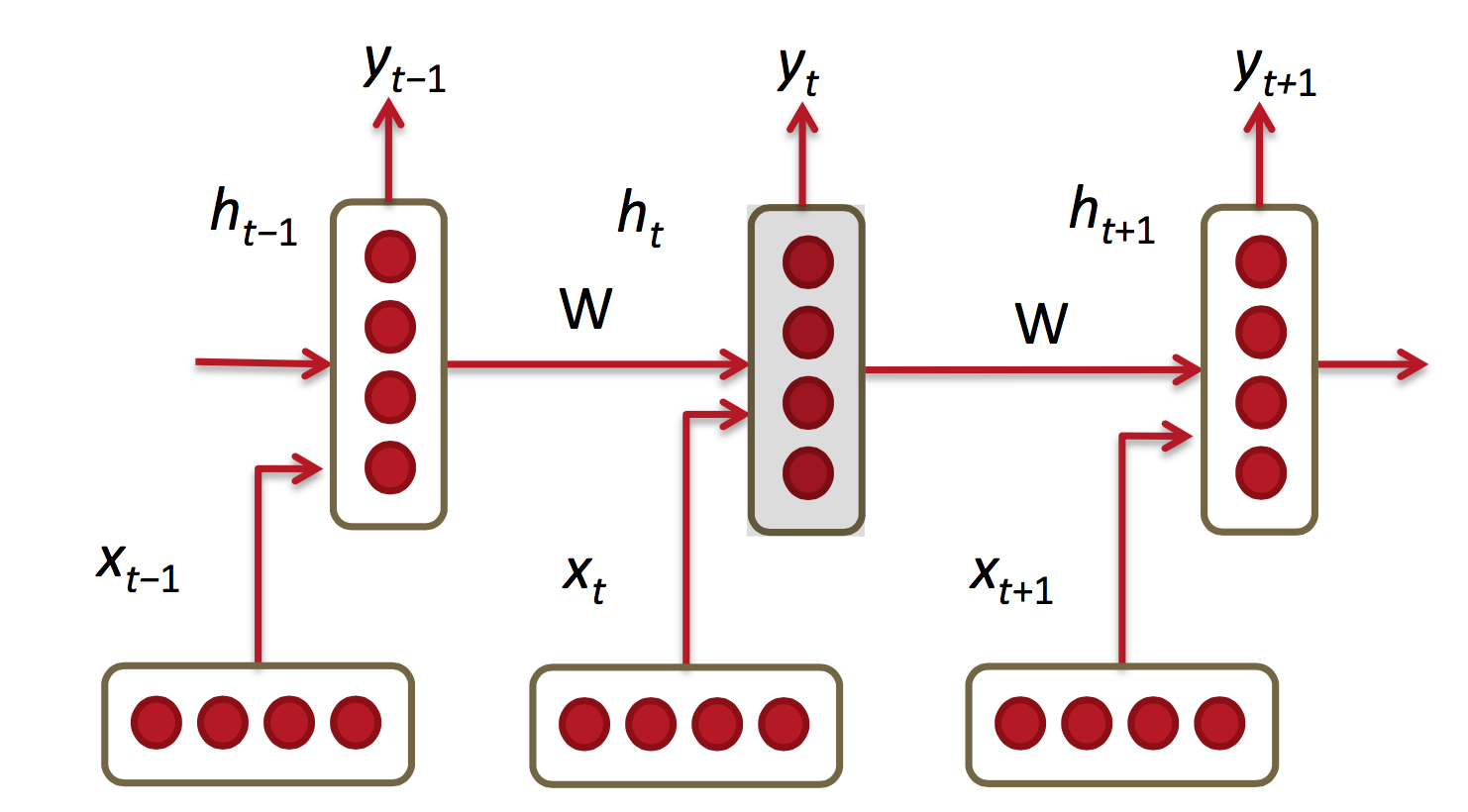
序列样本一般分为:一对多(生成图片描述),多对一(视频解说,文本归类),多对多(语言翻译)。RNN不仅能够处理序列输入,也能够得到序列输出,这里的序列指的是向量的序列。RNN学习来的是一个程序,也可以说是一个状态机,不是一个函数。
二、序列预测
1.下面以序列预测为例,介绍RNN网络。下面来描述这个问题。
(1)输入的是时间变化向量序列 x t-2 , x t-1 , x t , x t+1 , x t+2
(2)在t时刻通过模型来估计
![]()
(3)问题:对内部状态和长时间范围的场景难以建模和观察
(4)解决方案:引入内部隐含状态变量
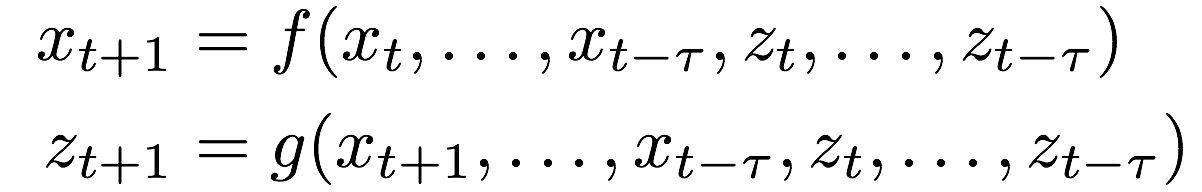
2.序列预测模型
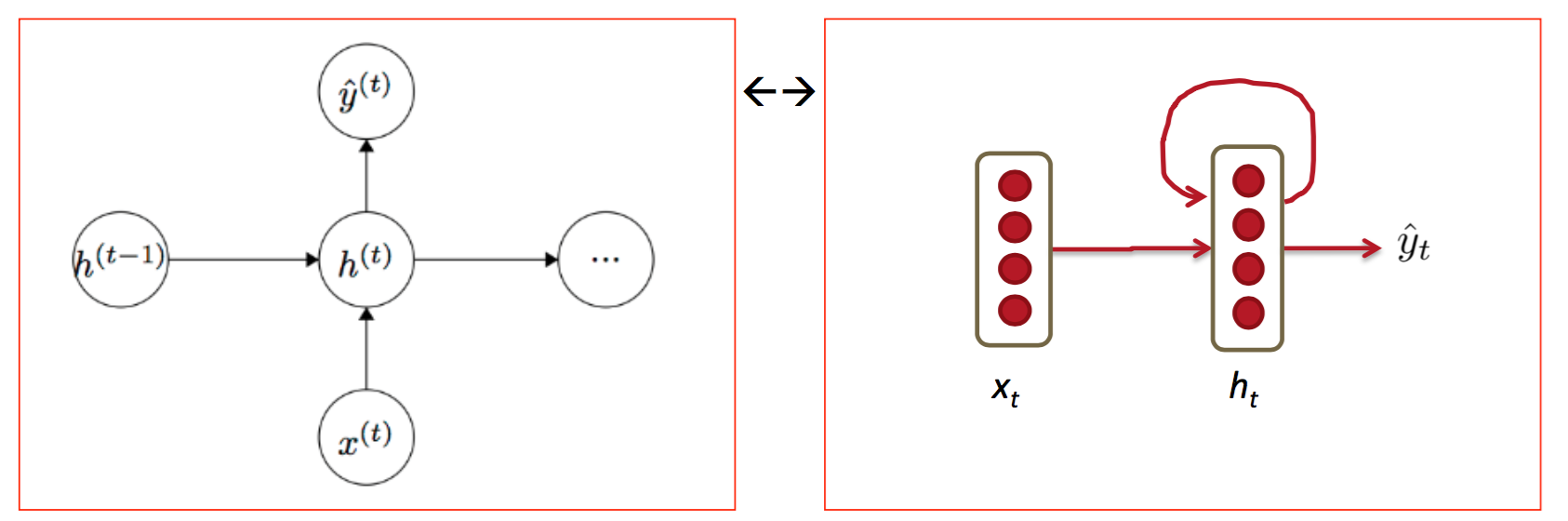
它与CNN网络的区别可以这样理解,它不仅需要本次的x最为输入,还要把前一次隐藏层作为输入,综合得出输出y
输入离散列序列: ![]()
在时间t的更新计算;

预测计算: ![]()
对于上图的各层参数说明如下:
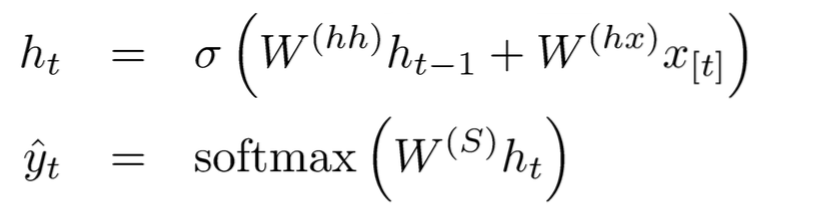
![]()
![]()
![]()
![]()
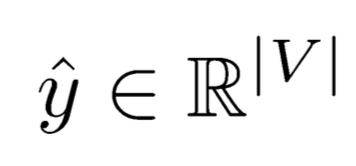
在整个计算过程中,W保持不变,h0在0 时刻初始化。当h0不同时,网络生成的东西也就不相同了,它就像一个种子。序列生成时,本次的输出yt会作为下一次的输入,这样源源不断的进行下去。
三、RNN的训练
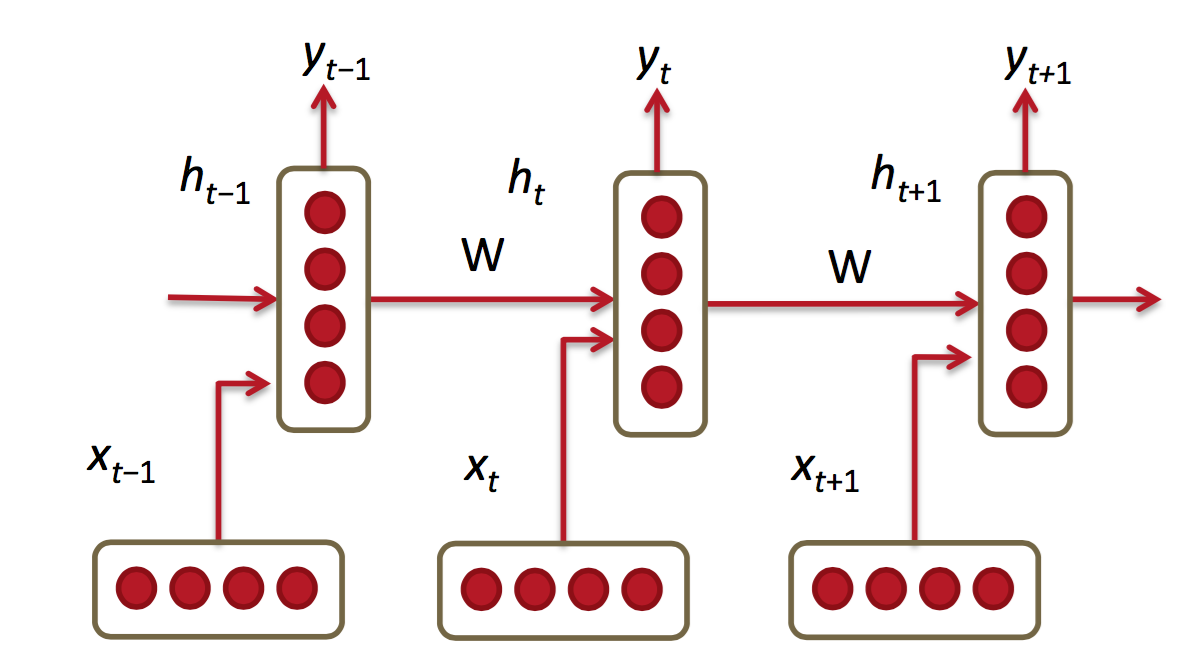

它做前向运算,相同的W要运算多次,多步之前的输入x会影响当前的输出,在后向运算过程中,同样W也不被乘多次。计算loss时,要把每一步的损失都加起来。
1.BPTT算法
(1)RNN前向运算
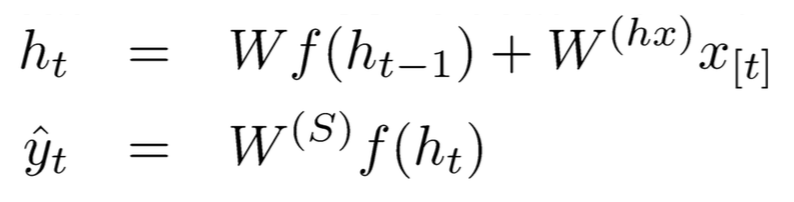
(2)计算w的偏导,需要把所有time step加起来
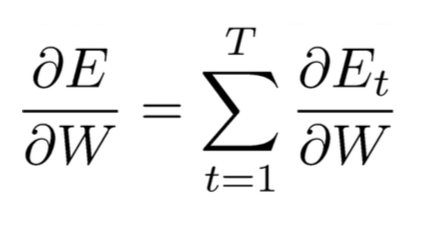
(3)计算梯度需要用到如下链式规则
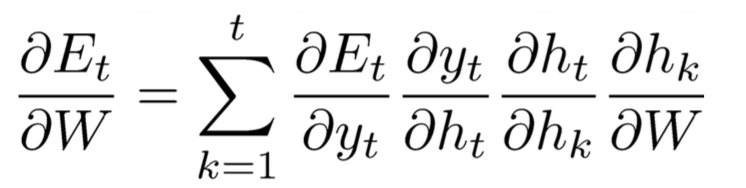
如上实在的dyt/dhk是没有计算公式的,下面来看看怎么计算这个式子
梳理一下我们的问题和已知,
计算目标:
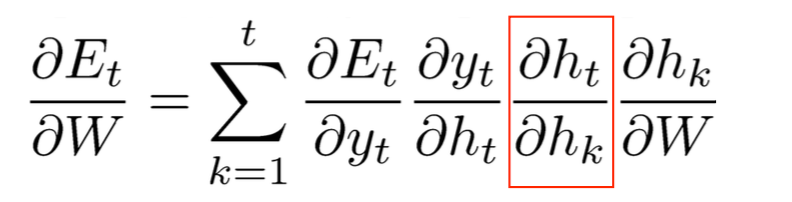
已知:
![]()
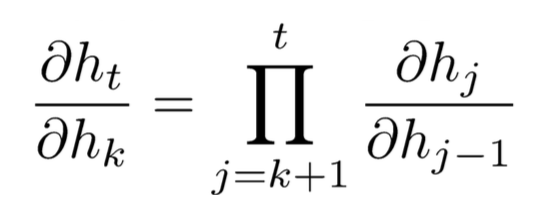
因此:

2.BPTT算法的梯度消失(vanishing)和梯度爆炸(exploding)现象分析
这里的消失和CNN等网络的梯度消失的原因是不一样的,CNN是因为隐藏层过多导致的梯度消失,而此处的消失是因为step过多造成的,如果隐层多更会加剧这种现象。
已知: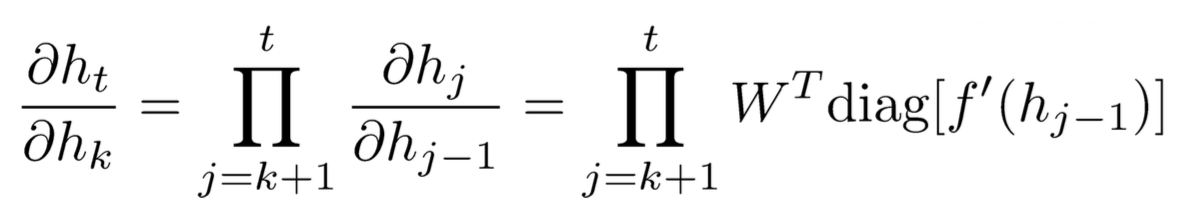
根据||XY||≤||X|| ||Y||知道:
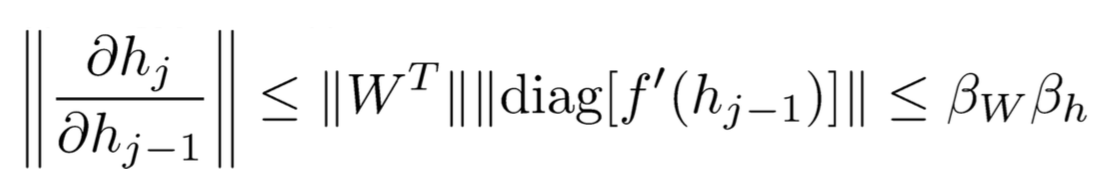
其中beta代表上限,因此:
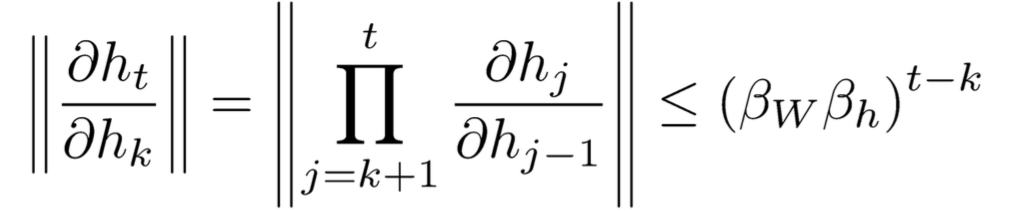
3.解决方案。
(1)clipping:不让梯度那么大,通过公式将它控制在一定的范围

(2)将tanh函数换为relu函数
但事实上直接用这种全连接形式的RNN是很少见的,很多人都在用LSTM
4.LSTM
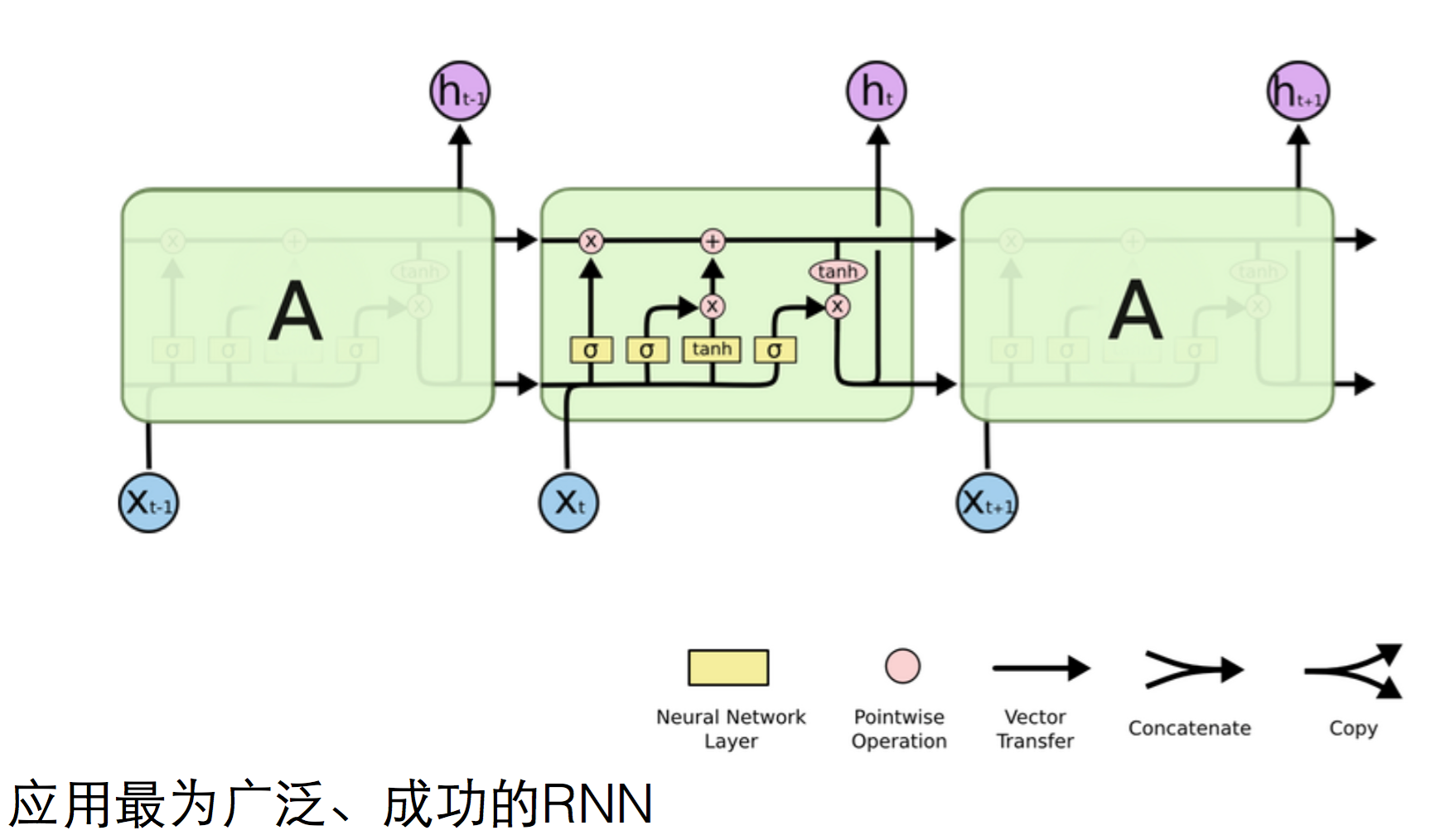
它的h层对下一个step有两个输入,除了h t-1外,多了一个c
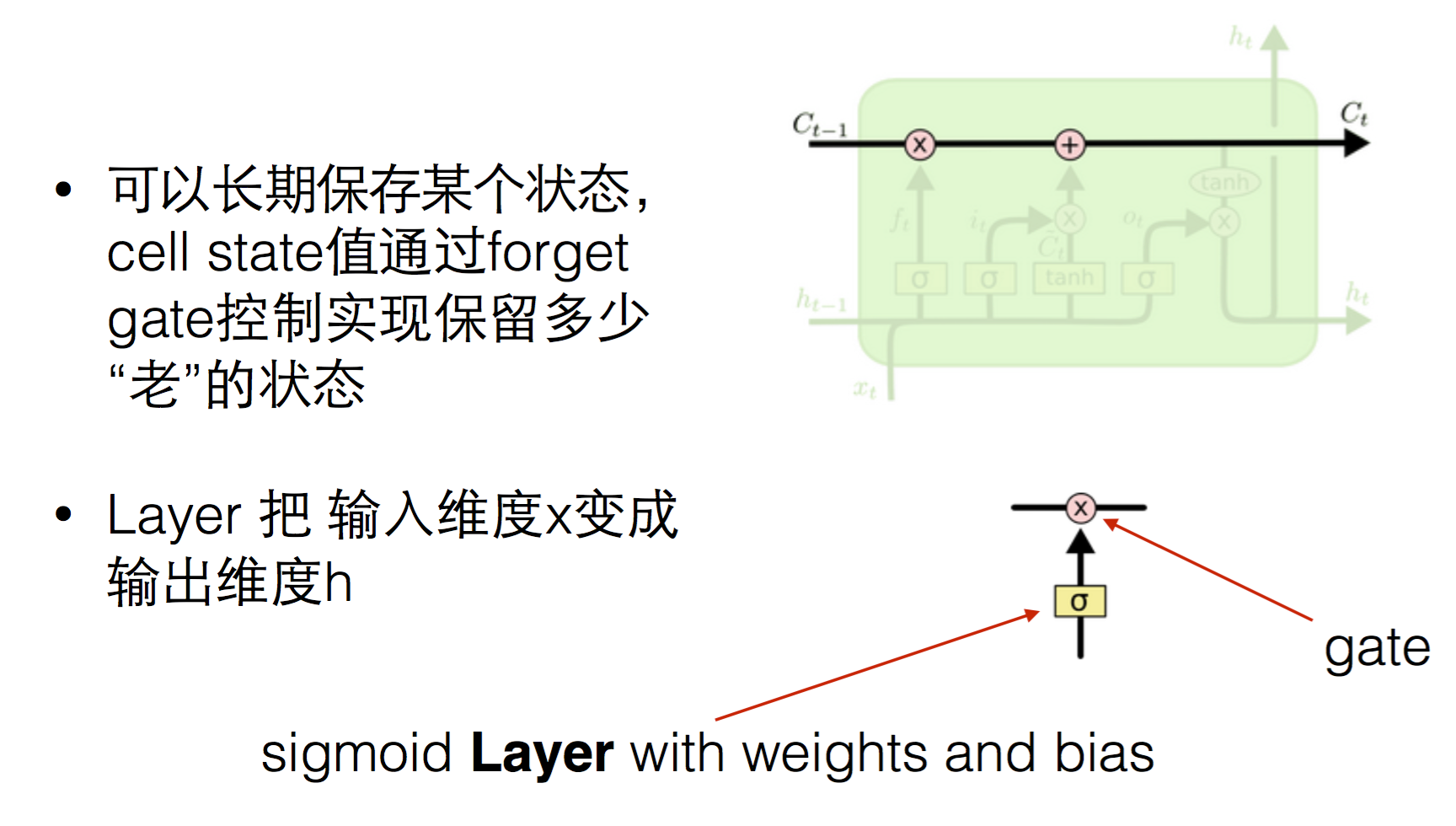
(1)forget / input unit
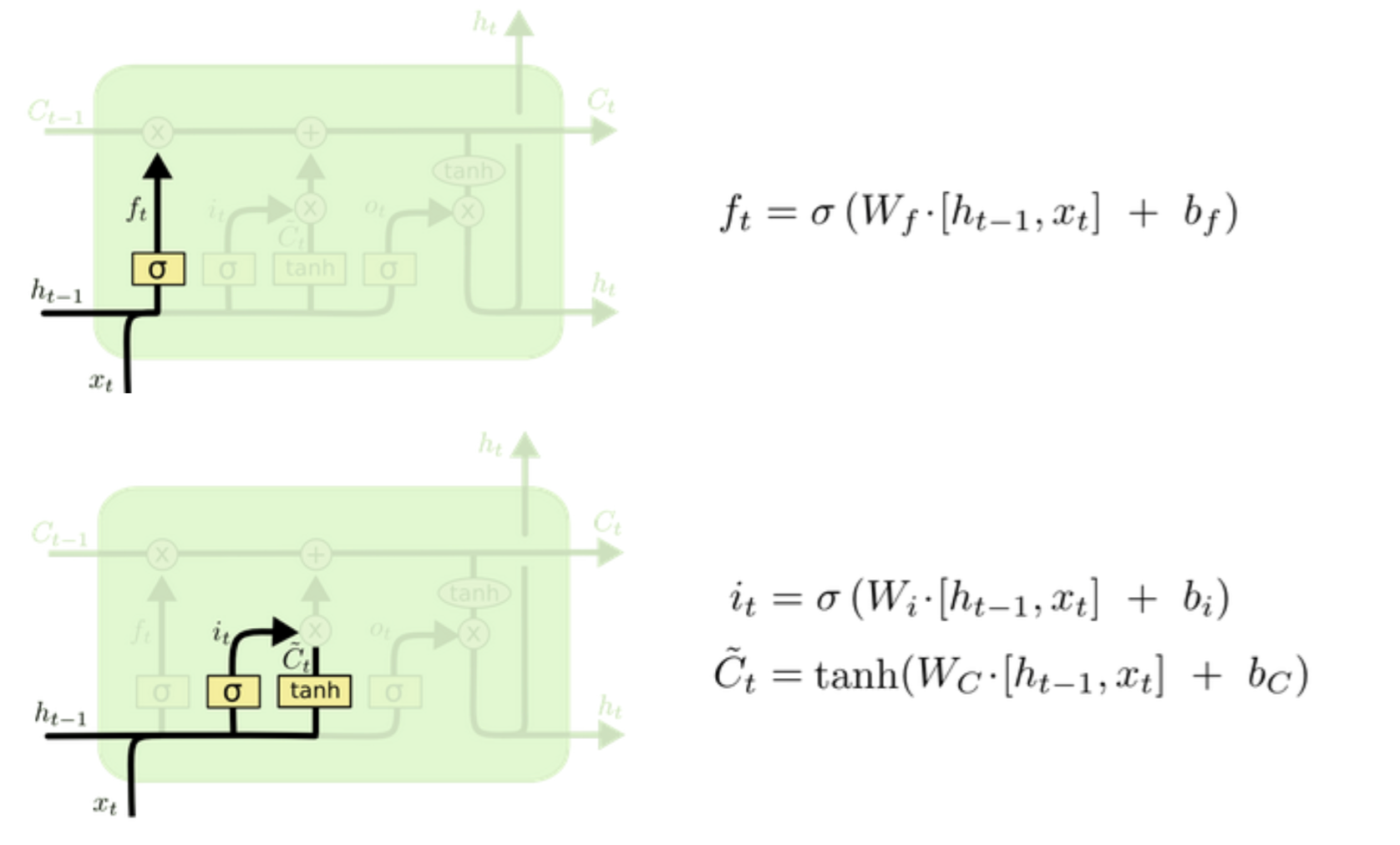
ft指的是对前一次的h要忘记多少,it为输入单元,表示本次要对c更新多少。
(2) update cell

因为ft最后是一个sigmoid函数,最后输出值大多为接近0或者1,也就是长短期记忆ct为-1到1的范围,所以它不止是累加,还是可能让其减小
(3)output
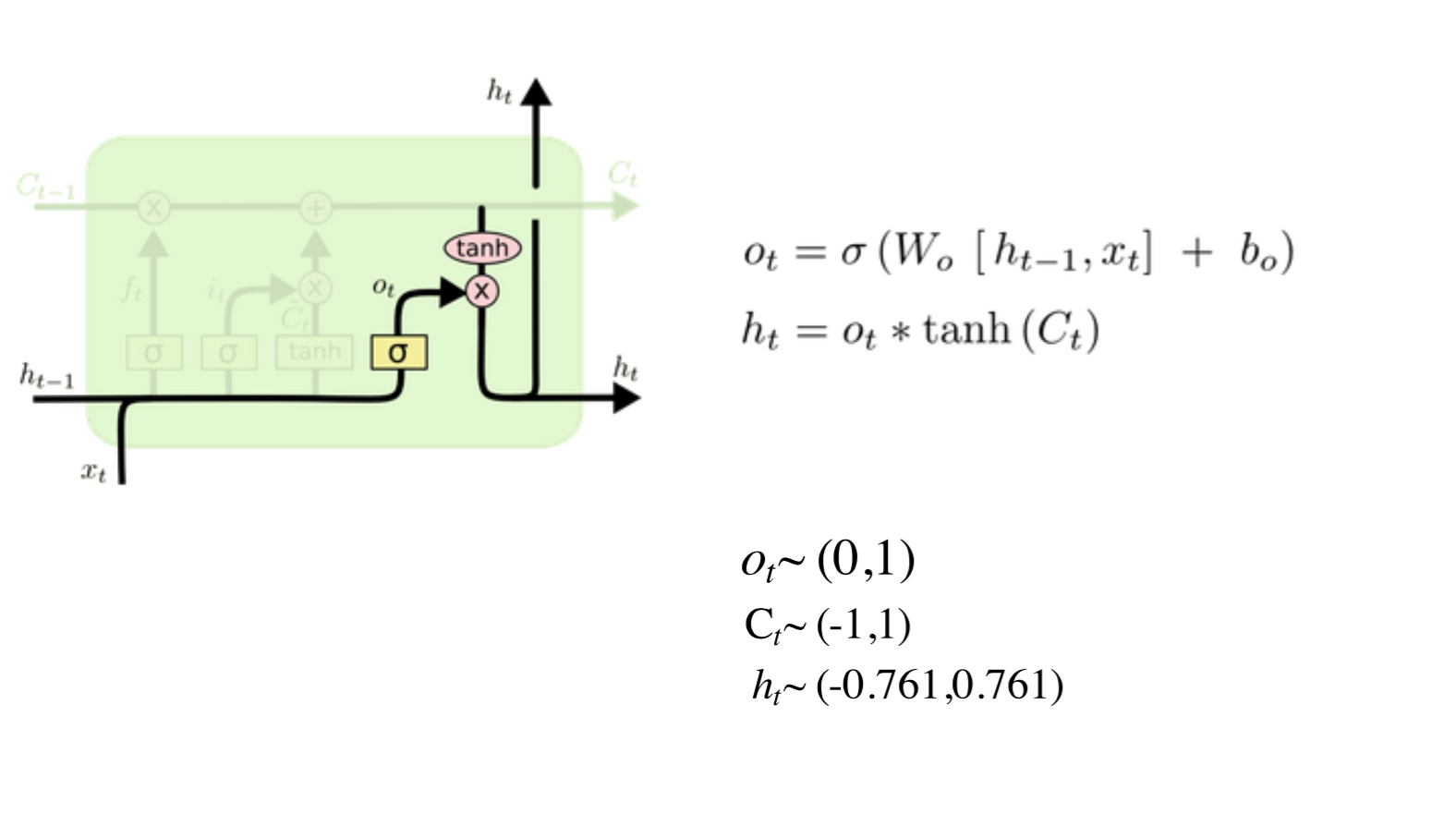
综上所述,LSTM的结构与公式是
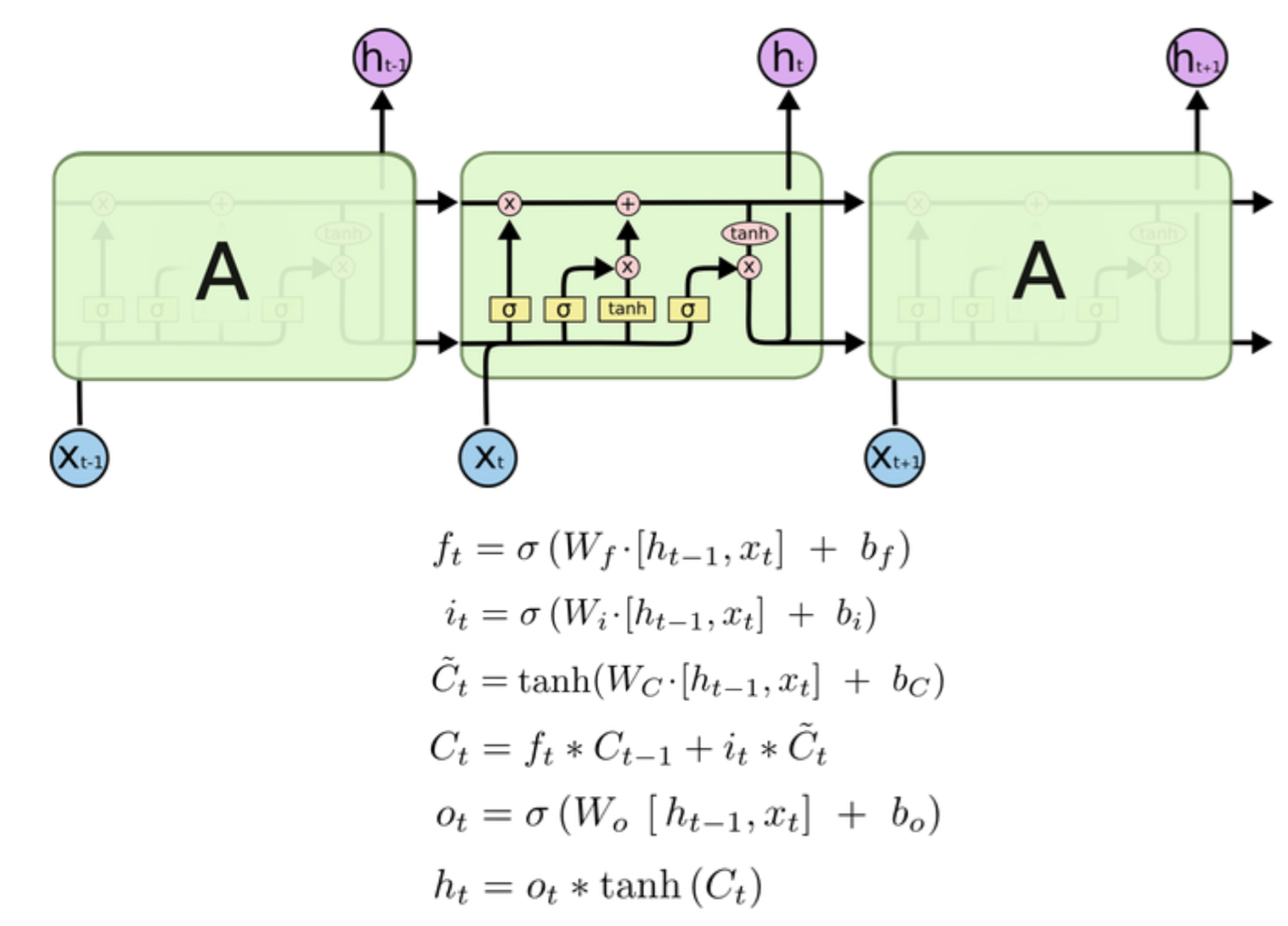
(4)LSTM的训练
不需要记忆复杂的BPTT公式,利用时序展开,构造层次关系,可以开发复杂的BPTT算法,同时LSTM具有定抑制梯度vinishing/exploding的特性。
(5)使用LSTM
将多个LSTM组合成层,网络中有多层,复杂的结构能够处理更大范围的动态性。
四、RNN的应用
1.learning to execute

序列数据的复杂性
(1)序列中相关距离可能很长
(2)需要有记忆功能
(3)代码中又有分支
(4)多种任务
如何训练
(1)样本的顺序:先易后难VS难易交替
(2)样本的类型:循环代码VS解析代码
2.字符语言模型:字符序列输入,预测下一个字符(https://github.com/karpathy/char-rnn)
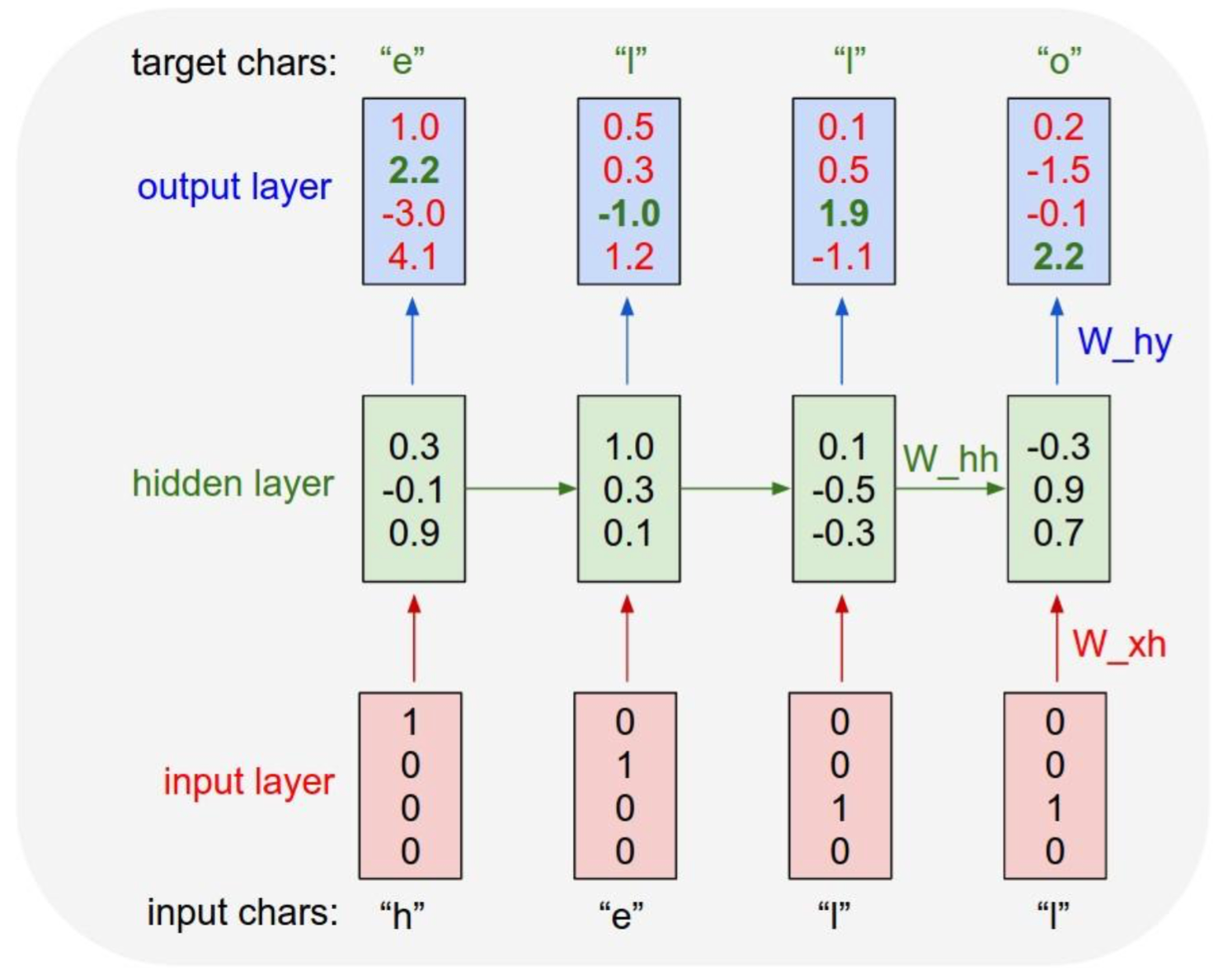
文本生成:在通过大量的样本训练好预测模型之后,我们可以利用这个模型来生产我们需要的文本
下面给出实现的代码;
"""
Minimal character-level Vanilla RNN model. Written by Andrej Karpathy (@karpathy)
BSD License
"""
import numpy as np
# data I/O
data = open('input.txt', 'r').read() # should be simple plain text file
chars = list(set(data))
data_size, vocab_size = len(data), len(chars)
print 'data has %d characters, %d unique.' % (data_size, vocab_size)
char_to_ix = { ch:i for i,ch in enumerate(chars) }
ix_to_char = { i:ch for i,ch in enumerate(chars) }
# hyperparameters
hidden_size = 100 # size of hidden layer of neurons
seq_length = 25 # number of steps to unroll the RNN for
learning_rate = 1e-1
# model parameters
Wxh = np.random.randn(hidden_size, vocab_size)*0.01 # input to hidden
Whh = np.random.randn(hidden_size, hidden_size)*0.01 # hidden to hidden
Why = np.random.randn(vocab_size, hidden_size)*0.01 # hidden to output
bh = np.zeros((hidden_size, 1)) # hidden bias
by = np.zeros((vocab_size, 1)) # output bias
def lossFun(inputs, targets, hprev):
"""
inputs,targets are both list of integers.
hprev is Hx1 array of initial hidden state
returns the loss, gradients on model parameters, and last hidden state
"""
xs, hs, ys, ps = {}, {}, {}, {}
hs[-1] = np.copy(hprev)
loss = 0
# forward pass
for t in xrange(len(inputs)):
xs[t] = np.zeros((vocab_size,1)) # encode in 1-of-k representation
xs[t][inputs[t]] = 1
hs[t] = np.tanh(np.dot(Wxh, xs[t]) + np.dot(Whh, hs[t-1]) + bh) # hidden state
ys[t] = np.dot(Why, hs[t]) + by # unnormalized log probabilities for next chars
ps[t] = np.exp(ys[t]) / np.sum(np.exp(ys[t])) # probabilities for next chars
loss += -np.log(ps[t][targets[t],0]) # softmax (cross-entropy loss)
# backward pass: compute gradients going backwards
dWxh, dWhh, dWhy = np.zeros_like(Wxh), np.zeros_like(Whh), np.zeros_like(Why)
dbh, dby = np.zeros_like(bh), np.zeros_like(by)
dhnext = np.zeros_like(hs[0])
for t in reversed(xrange(len(inputs))):
dy = np.copy(ps[t])
dy[targets[t]] -= 1 # backprop into y. see http://cs231n.github.io/neural-networks-case-study/#grad if confused here
dWhy += np.dot(dy, hs[t].T)
dby += dy
dh = np.dot(Why.T, dy) + dhnext # backprop into h
dhraw = (1 - hs[t] * hs[t]) * dh # backprop through tanh nonlinearity
dbh += dhraw
dWxh += np.dot(dhraw, xs[t].T)
dWhh += np.dot(dhraw, hs[t-1].T)
dhnext = np.dot(Whh.T, dhraw)
for dparam in [dWxh, dWhh, dWhy, dbh, dby]:
np.clip(dparam, -5, 5, out=dparam) # clip to mitigate exploding gradients
return loss, dWxh, dWhh, dWhy, dbh, dby, hs[len(inputs)-1]
def sample(h, seed_ix, n):
"""
sample a sequence of integers from the model
h is memory state, seed_ix is seed letter for first time step
"""
x = np.zeros((vocab_size, 1))
x[seed_ix] = 1
ixes = []
for t in xrange(n):
h = np.tanh(np.dot(Wxh, x) + np.dot(Whh, h) + bh)
y = np.dot(Why, h) + by
p = np.exp(y) / np.sum(np.exp(y))
ix = np.random.choice(range(vocab_size), p=p.ravel())
x = np.zeros((vocab_size, 1))
x[ix] = 1
ixes.append(ix)
return ixes
n, p = 0, 0
mWxh, mWhh, mWhy = np.zeros_like(Wxh), np.zeros_like(Whh), np.zeros_like(Why)
mbh, mby = np.zeros_like(bh), np.zeros_like(by) # memory variables for Adagrad
smooth_loss = -np.log(1.0/vocab_size)*seq_length # loss at iteration 0
while True:
# prepare inputs (we're sweeping from left to right in steps seq_length long)
if p+seq_length+1 >= len(data) or n == 0:
hprev = np.zeros((hidden_size,1)) # reset RNN memory
p = 0 # go from start of data
inputs = [char_to_ix[ch] for ch in data[p:p+seq_length]]
targets = [char_to_ix[ch] for ch in data[p+1:p+seq_length+1]]
# sample from the model now and then
if n % 100 == 0:
sample_ix = sample(hprev, inputs[0], 200)
txt = ''.join(ix_to_char[ix] for ix in sample_ix)
print '----
%s
----' % (txt, )
# forward seq_length characters through the net and fetch gradient
loss, dWxh, dWhh, dWhy, dbh, dby, hprev = lossFun(inputs, targets, hprev)
smooth_loss = smooth_loss * 0.999 + loss * 0.001
if n % 100 == 0: print 'iter %d, loss: %f' % (n, smooth_loss) # print progress
# perform parameter update with Adagrad
for param, dparam, mem in zip([Wxh, Whh, Why, bh, by],
[dWxh, dWhh, dWhy, dbh, dby],
[mWxh, mWhh, mWhy, mbh, mby]):
mem += dparam * dparam
param += -learning_rate * dparam / np.sqrt(mem + 1e-8) # adagrad update
p += seq_length # move data pointer
n += 1 # iteration counter