题目一
竹筒有20根签,10根白色,10根红色。抽取10根颜色一致可获得100元奖励,抽取9根颜色一致可获得50元奖励,但是抽取红色5根白色5根就损失50元,问这游戏是否值得参与?原因?
解:
这是典型的组合数求期望问题。设事件‘抽取10根颜色一致’为A,事件‘抽取9根颜色一致’为B,事件‘抽取红色5根白色5根‘为C。
根据组合数公式
C(m.n) = m!/(n!*(m-n)!)
求得事件A的概率P(A) = C(10,10)*2/C(20,10) = 0.00001082508822446903 ;
事件B的概率P(B) = C(10,9)*C(10,1)*2/C(20,10) = 0.001082508822446903;
事件C的概率P(C) = C(10,5)*C(10,5)/C(20,10) = 0.34371820130334063;
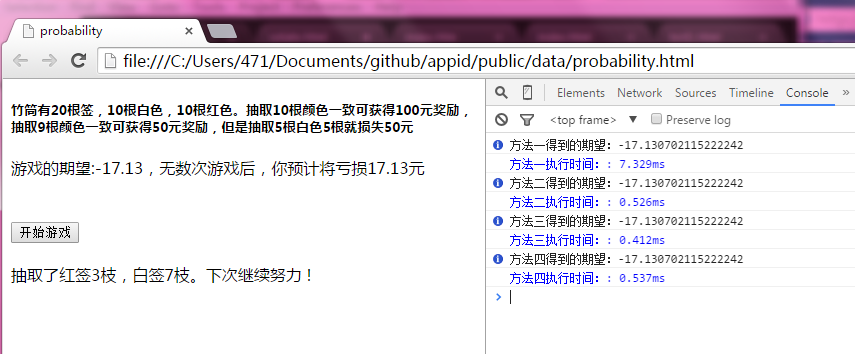
期望 = P(A)*100 + P(B)*50+P(C)*(-50) = -17.130702115222242;
结论,期望低于0。游戏无数次后,最终会亏损17.13元,该游戏不值得玩。
下面我们使用程序实现该游戏,并且提供求期望的函数。
第一个思考,如何高效求出概率,
第二个思考,如何有效地模拟用户抽签的情况,
第三个思考,如何统计抽签结果呢,
。。。。。

最后想想,万一日后用户需要修改游戏规则呢
完成整个模拟,需要实现四个模块:
第一部分,制定游戏规则和奖励规则
第二部分,计算期待
第三部分,获取一次游戏结果
第四部分,根据奖励规则,统计结果
打代码总是很愉快地,啦啦啦~~~


1 function Probability(){
2
3 //--------------------1,制定规则
4
5 //抽奖箱中的包含的签种类和数量
6 this.typeColor = {
7 'red': 10,
8 'white':10
9 };
10 //抽取数量
11 this.extractNum = 10;
12 //可能性,和收益对应表
13 this.possibility = {
14 '10' : 100,
15 '9' : 50,
16 '5' : -50
17 },
18
19
20 //--------------------2,计算期待
21 this.getExpectation = function(){
22
23 //暂时省略这一部分代码,下面我们一同探讨这一部分代码如何优化
24 return (-17.130702115222242).toFixed(2);
25 };
26 //-------------------3,获取一次游戏结果
27 this.playGame = function(){
28 var _a = [] ;//空抽奖箱,存储所有的球
29 var _r = []; //‘抽奖结果’
30 for( a in this.typeColor){
31 for(var i=0;i<this.typeColor[a];i++){
32 _a.push(a);
33 }
34 }//将签放入抽奖箱
35
36
37 //遍历,开始抽奖,
38 for(var i=0;i<10;i++){
39 //抽取特定一个球
40 var _i = Math.round(Math.random()*(_a.length-1));
41 //将抽出的球,放入‘抽奖结果’中
42 _r.push(_a[_i]);
43 //移除抽奖箱中刚被抽取的球
44 _a.splice(_i,1);
45 }
46 return _r;
47 };
48
49 //-------------------4,统计结果
50 this.getResult = function(arr){
51 //统计各种球的结果
52 var _r = {};
53 for( k in arr){
54 _r[arr[k]]? _r[arr[k]]++:_r[arr[k]] = 1;
55 }
56
57 //统计收益
58 for(p in _r){
59 for(k in this.possibility){
60 if(_r[p] == k){
61 _r.earnings = this.possibility[k];//价格
62 }
63 }
64 }
65 return _r;
66 }
67 }
下面我们一起思考求期望这一部分如何逐步优化:
尝试一,只完成基本的题目要求
1 function probability1(){
2 //通用C函数
3 //C(m.n) = m!/(n!*(m-n)!)
4 function C(a,b){
5 var _n=1,_d=1;//分子,分母
6 for(var i=a;i>0;i--)
7 _n *=i;
8 for(var i=b;i>0;i--)
9 _d *=i;
10 for(var i=1,j=(a-b);j>0;i++,j--)
11 _d *= i;
12 return _n/_d;
13 }
14 return C(10,10)*2/C(20,10)*100+//抽取10根相同颜色的概率*100
15 C(10,9)*C(10,1)*2/C(20,10)*50+//抽取9根相同颜色的概率*50
16 C(10,5)*C(10,5)/C(20,10)*(-50);//抽取5根相同颜色的概率*(-50)
17
18 }
仔细观察,好多组合数是被重复计算的,例如,C(10,10)和C(20,10)等等,可否用一个变量存储已经计算过的组合数,下次求相同的组合数的时候可以从静态变量中获取而不需要重复计算。
尝试二,在尝试一的基础上避免计算重复的C
1 function probability2(){
2 //通用C函数
3 function C(a,b){
4 var _n=1,_d=1;
5 if(!resOfC[a+','+b]){
6 var _n=1,_d=1;//分子,分母
7 for(var i=a;i>0;i--)
8 _n *=i;
9 for(var i=b;i>0;i--)
10 _d *=i;
11 for(var i=1,j=(a-b);j>0;i++,j--)
12 _d *= i;
13 return _n/_d;
14
15 }else{
16 return resOfC[a+','+b];
17 }
18 }
19
20 var resOfC = {}; //一个新的临时数组,存储可能出现的结果
21 //如果之前计算过C(10,10),可以直接从
22 console.info(C(10,10)*2/C(20,10));
23 console.info(C(10,9)*C(10,1)*2/C(20,10));
24 console.info(C(10,5)*C(10,5)/C(20,10));
25 return C(10,10)*2/C(20,10)*100+
26 C(10,9)*C(10,1)*2/C(20,10)*50+
27 C(10,5)*C(10,5)/C(20,10)*(-50);
28
29 }
然而,判断组合数是否重复计算并不是重点。有数学公式C(m,n) = C(m,m-n),我们计算C(10,9)可以转换为计算C(10,1),以提高计算效率。
尝试三,在尝试一的基础上判断a/2和b的大小,例如对于C(10,9),直接计算C(10,1)
1 function probability3(){
2 //通用C函数
3 function C(a,b){
4 var _n=1,_d=1;//分子,分母
5
6 if(b>a/2)
7 b = a-b;
8
9 for(var i=a;i>0;i--)
10 _n *=i;
11 for(var i=b;i>0;i--)
12 _d *=i;
13 for(var i=1,j=(a-b);j>0;i++,j--)
14 _d *= i;
15 return _n/_d;
16 }
17
18 var resOfC = {}; //一个新的临时数组,存储可能出现的结果
19 //如果之前计算过C(10,10),可以直接从
20 return C(10,10)*2/C(20,10)*100+
21 C(10,9)*C(10,1)*2/C(20,10)*50+
22 C(10,5)*C(10,5)/C(20,10)*(-50);
23
24 }
学过组合数的同学都知道,有数学公式C(n,k)=C(n-1,k)+C(n-1,k-1) ,
我们先从C(0,0)算起,然后C(1,0),C(1,1),C(2,0),C(2,1),C(2,2)......C(n,k),仔细观察,其实求组合数的问题由交叠的子问题构成。
第一时间想到的是使用递归关系包含子问题和大问题具有的相同形式,但由于子问题具有交叠,用递归方法解决代价很大,我们可以考虑使用动态规划来求解。
对每个交叠的子问题只求解一次,并把结果存储在记录表中,最后得出原始问题的解。
尝试四,利用递归和动态规划来求解组合数
存在C(n,k)=C(n-1,k)+C(n-1,k-1) ,建立一张表,我们对数据进行动态更新,即每一次迭代,我们都去根据公式计算出合适的值。
1 function probability3(){
2 //C(a,b)=C(a-1,b-1)+C(a-1,b)
3 //通用C函数
4 function C(a,b){
5 if(b==0){
6 return 1;
7 }
8 var temp = [];//
9 for (var i = 0; i < a; i++) {
10 temp[i] = [];
11 temp[i][0] = 1;//每行首尾为1
12 temp[i][i+1] = 1;//每行末尾为1
13
14 for (var j=1;j<=i;j++) {
15 temp[i][j] =temp[i-1][j-1]+temp[i-1][j];////计算第i行第j列的值
16 }
17 }
18 return temp[a-1][b];
19 }
20 return C(10,10)*2/C(20,10)*100+
21 C(10,9)*C(10,1)*2/C(20,10)*50+
22 C(10,5)*C(10,5)/C(20,10)*(-50);
23 }
源码及游戏演示测试地址:http://lovermap.sinaapp.com/probability.html
效果图:
题目二
眼前有两块100px*100px的两块div,分别距离我们10m和7m,但是由于视觉差,我们只看到最靠近我们的一块板。用鼠标模拟我们的运动轨迹,鼠标右移类似于我们往右侧行走。请模拟实现我们右移,所看到两块div形态变换。
一开始,我脑海中的构想:

假设100px=4cm,即半径等于85cm=>2125px。由于时间的关系,就直接把草稿拍照放上来,雅蠛蝶,真的好复杂:

我们围绕小圈圈,想看到后面的div。在我们接近圆边东方这个点的过程中,前面的div将会不要断缩小,而后面的div将会不断放大。但是鼠标移动npx,而div会放大mpx,需要集合详细的三角函数和反三角函数计算。好啦没问题来了,怎么算D1和D2

于是我开始不断恶补各种高中三角知识。。。。。
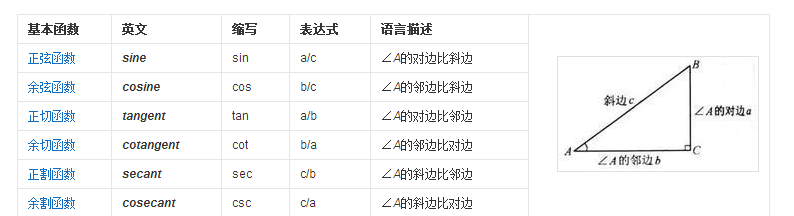
先补一下三角函数的基础知识
再补充一下javascript关于三角函数的方法
Math.cos(x) X的余弦函数 Math.sin(x) X的正弦函数 Math.tan(x) X的正切函数 Math.acos(y) X的反余弦函数 Math.asin(y) X的反正弦函数 Math.atan(y) X的反正切函数
折腾大半个晚上了,为什么还算不出来,难道真的是我理解错了 好咯好咯~~重新再想想
好咯好咯~~重新再想想
秉承“怎么简单怎么算”的原则,我重新理解了一次题目。。。。
10米和7米这两个数值如果转换为像素将不利于计算,出来的效果也不太乐观,我将它们分别改成了10cm和7cm了。
嗯嗯,应该是这样子了

假设人行走a cm,我们可以通过a来表示D1和D2的长度,期间使用到相似三角形、三角形面积公式等原理,完全不需要三角函数和反三角函数。剩下的就不难了
1 var $ = function(id){
2 return typeof id == 'string' ? document.getElementById(id) : id;
3 };
4 //计算前面板初始宽度
5 $("box1").style.width = 28/Math.sqrt(65)*30+'px';
6 (function(o){
7 if(o){var o = $(o);}else{return false;};
8 var d = document,x,y;
9 o.onselectstart = function(){return false;};
10 o.onmousedown = function(e){
11 e = e || window.event;
12 x = e.clientX-o.offsetLeft;
13 d.onmousemove = function(e){
14 e = e || window.event;
15 var a = e.clientX - x;
16
17 //小圆点在虚线范围内可拖拽
18 if(a>=0 && a<90){
19 o.style.left = e.clientX - x + "px";
20 var Div1 = 28/Math.sqrt(65+8*a);
21 var Div2 = (9/7)*a/Math.sqrt((9/49)*a*a+9);
22 $("box1").style.width = Div1*30+'px';
23 $("box2").style.width = Div2*30+'px';
24 }
25
26 };
27 d.onmouseup = function(){ d.onmousemove = null; };
28 };
29 })('origin');
源码及演示地址:http://lovermap.sinaapp.com/rotate.html
 拖动小黑点后->
拖动小黑点后->
总结
第一点,面试前千万不要熬夜,千万不要熬夜,千万不要熬夜!!!重要的事情要说三遍,面试答题的时候,脑袋满满的困意和饿意,将会造成悲惨的结局。
第二点,注意要把问题细化,着手解决问题前,应该根据题目所给的条件,将问题拆分成为若干小问题,然后针对性地根据逐一解决。
第三点,避免先入为主。一开始认为问题很难,不断深究,最后很容易把自己逼得走投无路。当问题暂时无法解决的时候,回到最初的问题,重新分析,换一个角度,将会有新想法。
参考链接

