遮挡判断
Time Limit: 10000/3000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 910 Accepted Submission(s):
295
Problem Description
在一个广场上有一排沿着东西方向排列的石柱子,阳光从东边以一定的倾角射来(平行光)。有的柱子可能被在他东边的高大的柱子的影子给完全遮挡住了。现在你要解决的问题是求出有多少柱子是没有被完全遮挡住的。
假设每个石柱子是一根细棒,而且都垂直于地面摆放。
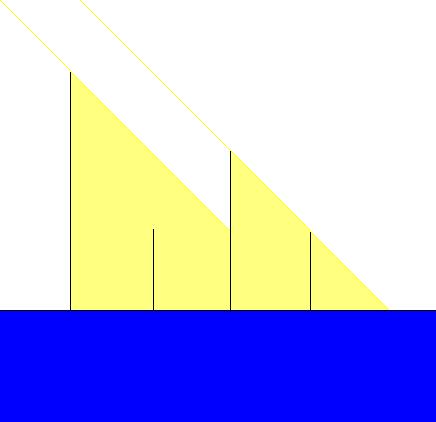
假设每个石柱子是一根细棒,而且都垂直于地面摆放。

Input
输入包含多组数据。每组数据第一行是一个整数N(0<N<=100000),表示柱子的个数。N=0代表输入结束。接下来有N行,每行是两个整数,分别给出每根柱子的水平位置X和高度H(X越大,表示越在西边,0<=X<=10000000,0<H<=10000000保证不会有两根柱子在同一个X坐标上)。最后有一行,以分数的形式给出太阳光与地面的夹角的正切值T/A(1<=A,T<=10)。
Output
对每组数据,输出包含所求数目的一行。
Sample Input
4
0 3
3 1
2 2
1 1
1/1
0
Sample Output
2
提示:
输入数据很多,请用scanf代替cin。
Source
Recommend
暴力判断一下。 前边木条高度减去当前木条高度再减去中间间隔所对应高度。
#include <cstdio> #include <cstring> #include <iostream> #include <algorithm> using namespace std; const int N = 100001; struct Posi{ double x, y; }Num[N]; bool cmp(Posi x, Posi y){ return x.x < y.x; } int main(){ int T; while(~scanf("%d", &T), T){ for(int i = 0; i < T; i++) scanf("%lf%lf", &Num[i].x, &Num[i].y); double tana, tanb; scanf("%lf/%lf", &tana, &tanb); sort(Num, Num+T, cmp); //按位置排一下序。 double Max = Num[0].y; int sum = 0; for(int i = 1; i < T; i++){ if(Max-Num[i].y-(Num[i].x-Num[i-1].x)*tana/tanb >= 0){ //更新Max值及计算被挡木条数目; sum++; Max = Max - (Num[i].x-Num[i-1].x)*tana/tanb; } else Max = Num[i].y; } printf("%d ", T-sum); } return 0; }