
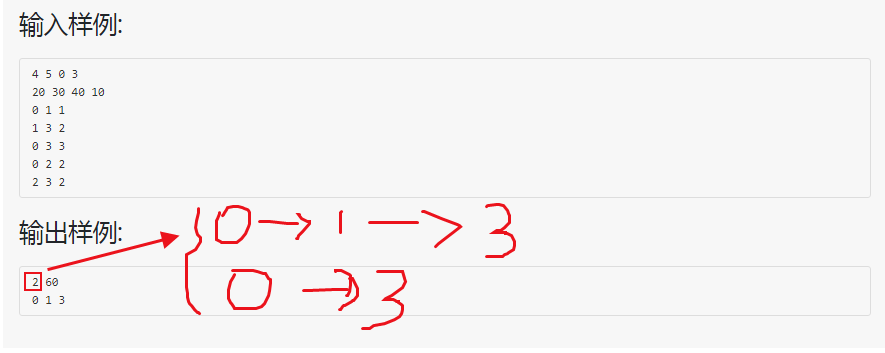
解题思路:
用dijkstra算法求单源最短路径,再用数组记录当前结点为终点时,最短路径的上一个结点的编号。
#include <stdio.h> #include <string.h> #define MaxVex 500+5 #define INF 0x3f3f3f3f int G[MaxVex][MaxVex];//图-邻接矩阵 int visit[MaxVex]= {0}; //标记访问数组 int path[MaxVex]= {-1}; //途经路径 int cnt[MaxVex];//最短路径数量 int dist[MaxVex];//最短路径 int rsc[MaxVex];//各城市救援队伍数量 int rs[MaxVex];//当前救援队伍数量 int Nv,Ne,s,d; //图的初始化 void Init() { int i,v1,v2,x; for(i=0; i<Nv; i++) { scanf("%d",&rsc[i]); rs[i]=rsc[i]; } memset(G,INF,sizeof(G)); for(i=0; i<Nv; i++) { G[i][i]=0; } for(i=0; i<Ne; i++) { scanf("%d %d %d",&v1,&v2,&x); G[v1][v2]=x; G[v2][v1]=G[v1][v2]; } for(i=0; i<Nv; i++) { dist[i]=G[s][i]; cnt[i]=1; } }
//单源最短路径 void Dijkstra() { visit[s]=1; int i,w,j; int flag=0; for(j=0; j<Nv; j++) { int MIN=INF; for(i=0; i<Nv; i++) { if(!visit[i]&&dist[i]<MIN) { flag=1; MIN=dist[i]; w=i; } } if(flag) { flag=0; visit[w]=1; for(i=0; i<Nv; i++) { if(!visit[i]&&MIN+G[w][i]<dist[i]) { dist[i]=MIN+G[w][i]; path[i]=w; cnt[i]=cnt[w]; rs[i]=rsc[i]+rs[w]; } else if(!visit[i]&&G[w][i]+MIN==dist[i]) { cnt[i]=cnt[i]+cnt[w]; if(rs[i]<rsc[i]+rs[w]) { path[i]=w; rs[i]=rsc[i]+rs[w]; } } } } } } int main() { scanf("%d %d %d %d",&Nv,&Ne,&s,&d); int i; Init(); Dijkstra(); int road[MaxVex];//记录从S到D的路径中经过的城市编号 int t=0; i=d; while(i!=s) { road[t++]=i; i=path[i]; } road[t]=s; printf("%d %d ",cnt[d],rs[d]+rsc[s]); for(i=t; i>=0; i--) { if(i!=t) printf(" "); printf("%d",road[i]); } }