P3436 [POI2006]PRO-Professor Szu

P3436 [POI2006]PRO-Professor Szu

题目描述

n个别墅以及一个主建筑楼，从每个别墅都有很多种不同方式走到主建筑楼，其中不同的定义是（每条边可以走多次，如果走边的顺序有一条不同即称两方式不同）。

询问最多的不同方式是多少，以及有多少个别墅有这么多方式，按照顺序输出别墅编号。

如果最多不同方式超过了36500那么都视作zawsze

输入输出样例

输入样例#1： 

3 5
1 2
1 3
2 3
3 4
3 4

输出样例#1： 

4
1
1

这题反向建个图，缩个点，跑个topo就没了？显然没有这么容易，这里说一下题目的坑点。首先这个题目是要求从n+1号结点出发，那么如果n+1号点不能到达所有的结点会怎么样呢？

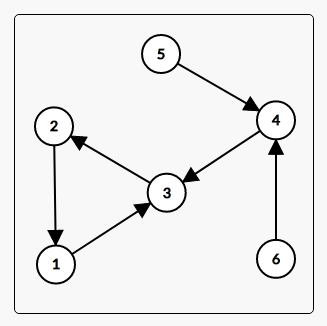
看上面这张图，假设这是我们的反向图，按理说我们应该从6号点开始topo，但是5号点自始至终都不会入队，所以说4号点的入度就不可能减到0，这样的话4号点就无法进行topo,那么这样的答案也肯定是错的。要解决这个问题也很简单，就是在缩点时只缩从n+1号点能到达的结点，然后再建新图，而且建的新图中不能含有从n+1号点不能到达的结点。

tarjan(n+1);//这里只从n+1号点开始缩点 
for(int i=1;i<=n+1;i++)
{
    if(!dfn[i]) continue;//如果某一个点是n+1号点无法到达的，那么就不能把这个点加到图中 
    for(int j=last[i];j;j=g[j].next)
    {
        int v=g[j].to;
        if(co[i]!=co[v])
        {
            add1(co[i],co[v]);
            de[co[v]]++;
        }
    }
}

但是这样还是A不了，这又是为啥呢？原来是自环惹的祸。

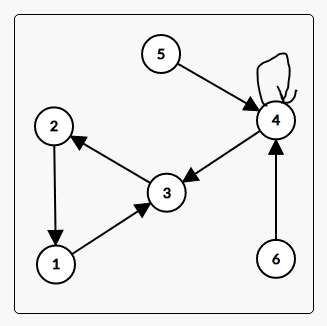
看上边的图，我们已经解决了五号点这个从起点无法到达的点的问题了，但是如果四号点给你来一个自环，那不好意思，你又挂了，要是按正常的缩点的话，四号点应该自己单独成为一个强联通分量，按理应该不需要管他，直接dp就好了，但是如果有自环，那么只要经过4号点，方案数就一定会变为正无穷，所以说，自环也是一定要考虑在内的，但是该怎么做呢，这个就更简单了，只需在读入的时候加个特判就好了，最后统计是把自环也当成环处理即可。

for(int i=1;i<=m;i++)
{
    aa=read();bb=read();
    if(aa==bb)
    b[aa]=1;//如果有自环，就标记一下； 
    add(bb,aa);
}

然而这样还是A不了，这究竟是为什么呢？后来经我计算发现36500*1000000=36500000000

然后就GG了，果断#define int long long，然后就A了……

真的是巨坑无比的一道题目。

#include<iostream>
#include<string>
#include<cmath>
#include<cstring>
#include<cstdio>
#include<stack>
#include<queue>
#define int long long 
#define maxn 2000005
using namespace std;

struct edge
{
    int next,to;
}g[maxn<<1],g1[maxn<<1];
int n,m,num,tot,col,num1,aa,bb,cnt,tott,pd,de[maxn],t[maxn];
long long ans;
long long f[maxn];
int last[maxn],dfn[maxn],low[maxn],co[maxn],last1[maxn],a[maxn],b[maxn],c[maxn];
stack<int>s;
stack<int>ss;

inline int read()
{
    char c=getchar();
    int x=1,res=0;
    while(c<'0'||c>'9')
    {
        if(c=='-')
        x=-1;
        c=getchar();
    }
    while(c>='0'&&c<='9')
    {
        res=res*10+(c-'0');
        c=getchar();
    }
    return x*res;
}

void add(int from,int to)
{
    g[++num].next=last[from];
    g[num].to=to;
    last[from]=num;
}

void add1(int from,int to)
{
    g1[++num1].next=last1[from];
    g1[num1].to=to;
    last1[from]=num1;
}

void tarjan(int u)
{
    dfn[u]=low[u]=++tot;
    s.push(u);
    for(int i=last[u];i;i=g[i].next)
    {
        int v=g[i].to;
        if(!dfn[v])
        {
            tarjan(v);
            low[u]=min(low[u],low[v]);
        }
        else if(!co[v])
        {
            low[u]=min(low[u],dfn[v]);
        }
    }
    if(low[u]==dfn[u])
    {
        col++;cnt=0;
        for(;;)
        {
            int x=s.top();s.pop();
            co[x]=col;
            cnt++;
            if(x==u) break;
        }
        a[col]=cnt;
    }
}

void topo()
{
    ss.push(co[n+1]);
    if(c[co[n+1]]==1)
    {
        f[co[n+1]]=36501;
    }
    else
    {
        f[co[n+1]]=1;
    }
    while(ss.size())
    {
        int u=ss.top();ss.pop();
        for(int i=last1[u];i;i=g1[i].next)
        {
            int v=g1[i].to;
            if(c[v]==1)
            {
                f[v]=36501;
            }
            else
            {
                f[v]+=f[u];
            }
            de[v]--;
            if(de[v]==0)
            ss.push(v);
        }
    }
}

signed main()
{
    n=read();m=read();
    for(int i=1;i<=m;i++)
    {
        aa=read();bb=read();
        if(aa==bb)
        b[aa]=1;//如果有自环，就标记一下； 
        add(bb,aa);
    }
    tarjan(n+1);//这里只从n+1号点开始缩点 
    for(int i=1;i<=n+1;i++)
    {
        if(!dfn[i]) continue;//如果某一个点是n+1号点无法到达的，那么就不能把这个点加到图中 
        for(int j=last[i];j;j=g[j].next)
        {
            int v=g[j].to;
            if(co[i]!=co[v])
            {
                add1(co[i],co[v]);
                de[co[v]]++;
            }
        }
    }
    for(int i=1;i<=n+1;i++)
    {
        if(b[i]==1)
        {
            c[co[i]]=1;
        }
        if(a[co[i]]>1)
        {
            c[co[i]]=1;
        }
    }
    topo();
    for(int i=1;i<=n;i++)
    {
        if(f[co[i]]>36500)
        {
            pd=1;
        }
        ans=max(ans,f[co[i]]);
    }
    if(pd==1)
    {
        printf("zawsze
");
        for(int i=1;i<=n;i++)
        {
            if(f[co[i]]>36500)
            {
                t[++tott]=i;
            }
        }
        printf("%d
",tott);
        for(int i=1;i<=tott;i++)
        {
            printf("%d ",t[i]);
        }
        return 0;
    }
    else 
    {
        printf("%lld
",ans);
        for(int i=1;i<=n;i++)
        {
            if(f[co[i]]==ans)
            t[++tott]=i;
        }
        printf("%d
",tott);
        for(int i=1;i<=tott;i++)
        {
            printf("%d ",t[i]);
        }
        return 0;
    }
}