看到数据范围,就想写一个线性复杂度的算法,一开始我是这样的:
#include<bits/stdc++.h> using namespace std; const int N=1e5+5; int n,a[N],ans,b[N]; int main() { scanf("%d",&n); for(int i=1;i<=n;i++) scanf("%d",&a[i]); b[1]=a[1]; for(int i=1;i<n;i++) b[i+1]=b[i]+i; for(int i=1;i<=n;i++) if(b[i]!=a[i]) ans++; cout<<ans; return 0; }
提交后只有50分(数据太水了,竟然拿到了50分)
这种做法显然是错误的,因为它只以1为基准构造了一个合法序列。例如当序列为
1 5 7 10 14时,如果按照上述做法,合法序列为:1,2,4,7,11 要修改4处。但显然这里只要修改一处即可。
于是就想到了正确的算法雏形:依次以每一个数为基准,统计修改次数,最后取最小值,就是正解。但显然这种做法是O(n^2)的,需要优化。
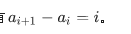
则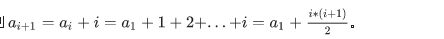
我们定义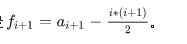
它得到的结果就是a[1]。
我们只需要遍历一遍原数组,求出每一个数的f,如果f相同,则意味着它们对应的a[1]相同,即它们处于同一个合法序列中。我们只要求出最多的相同的f的个数,就是合法值的个数。答案就是n-cnt.
#include<bits/stdc++.h> using namespace std; const int N=1e5+5; int n,a[N],f[N]; int main() { scanf("%d",&n); for(int i=1;i<=n;i++) scanf("%d",&a[i]); for(int i=1;i<=n;i++) { f[i]=a[i]-(i-1)*i/2; } sort(f+1,f+n+1); int len=1,ans=0; for(int i=2;i<=n;i++) { if(f[i]!=f[i-1]) { ans=max(ans,len); len=1; } else len++; } ans=max(ans,len); cout<<n-ans; return 0; }