题目描述
链接:https://ac.nowcoder.com/acm/contest/17/D?&headNav=www&headNav=acm
来源:牛客网
给定一张n个点,m条边的带权有向无环图,同时给定起点S和终点T,一共有q个询问,每次询问删掉某个点和所有与它相连的边之后S到T的最短路,询问之间互相独立(即删除操作在询问结束之后会立即撤销),如果删了那个点后不存在S到T的最短路,则输出-1。
题解
单源最短路一般采用的是dijkstra算法,堆优化的时间复杂度是(O(VlgV+E))
但是这道题是DAG,就不需要从dijkstra上考虑问题。从有向无环图的性质上思考这道题。
DAG:有向无环图
在DAG上求最短路最快(好)的方法是,先拓扑排序,再根据这个拓扑排序的序列枚举每条边,松弛更新后面的点。
可以这样做是因为当前点肯定由与它的前驱,并且拓扑序在其前面的点更新。这样就有了最优子结构,可以由类似动态规划的方法做出来。
这道题求出拓扑序之后,可以发现:
一个点删除后,如果还存在路径,应用于拓扑序上:肯定存在一条边跨过了这个点。
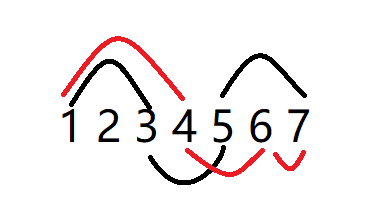
如图,如果4被删除,肯定由35构成新路径。
如果5被删除,肯定由46构成新路径。
删除后如果同时有两条边跨过了这个点:如下图的5,存在边37和边27跨过这个点,那就选择最优的路径。
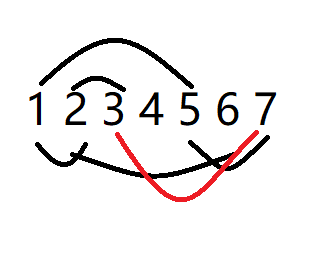
经过这条路径的次短路怎么求:s到这个点的最短路+边权+t到这个点的最短路(反图)
现在怎样有一个高效的方法快速得到跨过这个点的最短的路径?
线段树
从图中会发现,抽象出来,这个就是线段树的区间修改更新最小值,点查询的操作。
每条边((u,v))对((u+1,v-1))的区间有贡献,这个贡献就是经过((u,v))的次短路,可以通过正路径和反路径得出。
代码
#include <bits/stdc++.h>
#define ll long long
using namespace std;
const int maxn = 1e5 + 10;
int n;
struct edge{
int ed;
ll val;
};
struct graph{
int s,t;
int in[maxn],topIndex[maxn];
ll dis[maxn];
vector<edge>G[maxn];
void addEdge(int u,int v,int w){
in[v]++;
G[u].push_back(edge{v,w});
}
int arr[maxn],aIndex = 0;
void topSort(){
queue<int>que;
for(int i=1;i<=n;++i){
if(in[i] == 0){
que.push(i);
topIndex[i] = aIndex;
arr[aIndex++] = i;
}
}
while(!que.empty()){
int u = que.front();
que.pop();
for(edge tmp:G[u]){
if(--in[tmp.ed] == 0){
que.push(tmp.ed);
topIndex[tmp.ed] = aIndex;
arr[aIndex++] = tmp.ed;
}
}
}
}
void shortPath(){
memset(dis,-1,sizeof(dis));
dis[s] = 0;
for(int i = 0;i < aIndex;++i){
if(dis[arr[i]] == -1){
continue;
}
for(edge tmp:G[arr[i]]){
if(dis[tmp.ed] == -1 || dis[arr[i]] + tmp.val < dis[tmp.ed]){
dis[tmp.ed] = dis[arr[i]] + tmp.val;
}
}
}
}
}forwGraph,revGraph;
class SegmentTree{
public:
long long tag[maxn << 2];
void build(int l, int r, int rt){
tag[rt] = 1e18;
if (l == r) return;
int m = (l + r) >> 1;
build(l, m, rt << 1);
build(m + 1, r, rt << 1 | 1);
}
void update(int L, int R, long long val, int l, int r, int rt){
if (L <= l && r <= R){
tag[rt] = min(tag[rt], val);
return;
}
int m = (l + r) >> 1;
if (L <= m) update(L, R, val, l, m, rt << 1);
if (m < R) update(L, R, val, m + 1, r, rt << 1 | 1);
}
void query(int x, int l, int r, int rt, long long &ans){
ans = min(ans, tag[rt]);
if (l == r) return;
int m = (l + r) >> 1;
if (x <= m) query(x, l, m, rt << 1, ans);
else query(x, m + 1, r, rt << 1 | 1, ans);
}
}st;
void buildTree(){
for(int i=1;i<=n;++i){
for(edge tmp : forwGraph.G[i]){
ll disu = forwGraph.dis[i];
ll disv = revGraph.dis[tmp.ed];
int u = forwGraph.topIndex[i];
int v = forwGraph.topIndex[tmp.ed];
if(disu != -1 && disv != -1 && u + 1 < v){
st.update(u + 1,v - 1,disu + disv + tmp.val,1,n,1);
}
}
}
}
int main(){
int m,S,T;
scanf("%d%d%d%d",&n,&m,&S,&T);
for(int i=1,u,v,w;i <= m;++i){
scanf("%d%d%d",&u,&v,&w);
forwGraph.addEdge(u,v,w);
revGraph.addEdge(v,u,w);
}
forwGraph.s = S;
revGraph.s = T;
forwGraph.topSort();
forwGraph.shortPath();
revGraph.topSort();
revGraph.shortPath();
int Q;
scanf("%d",&Q);
st.build(1,n,1);
buildTree();
while(Q--){
int x;
scanf("%d",&x);
ll ans = 1e18;
if(forwGraph.dis[T] == -1){
puts("-1");
continue;
}
if(forwGraph.dis[x] == -1 || revGraph.dis[x] == -1){
printf("%lld
",forwGraph.dis[T]);
continue;
}
st.query(forwGraph.topIndex[x],1,n,1,ans);
if(ans == 1e18){
printf("-1
");
}else{
printf("%lld
",ans);
}
}
return 0;
}