打家劫舍 III

题目描述：

在上次打劫完一条街道之后和一圈房屋后，小偷又发现了一个新的可行窃的地区。这个地区只有一个入口，我们称之为“根”。 除了“根”之外，每栋房子有且只有一个“父“房子与之相连。一番侦察之后，聪明的小偷意识到“这个地方的所有房屋的排列类似于一棵二叉树”。 如果两个直接相连的房子在同一天晚上被打劫，房屋将自动报警。

计算在不触动警报的情况下，小偷一晚能够盗取的最高金额。

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/house-robber-iii
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

例1:

输入: [3,2,3,null,3,null,1]

     3
    / 
   2   3
        
     3   1

输出: 7 
解释: 小偷一晚能够盗取的最高金额 = 3 + 3 + 1 = 7.

　例2：

输入: [3,4,5,1,3,null,1]

     3
    / 
   4   5
  /     
 1   3   1

输出: 9
解释: 小偷一晚能够盗取的最高金额 = 4 + 5 = 9.

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/house-robber-iii
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

　解题思路：

方法一：暴力递归

为了便于理解，我将节点取名为：爷爷、父亲、孙子，如下图所示

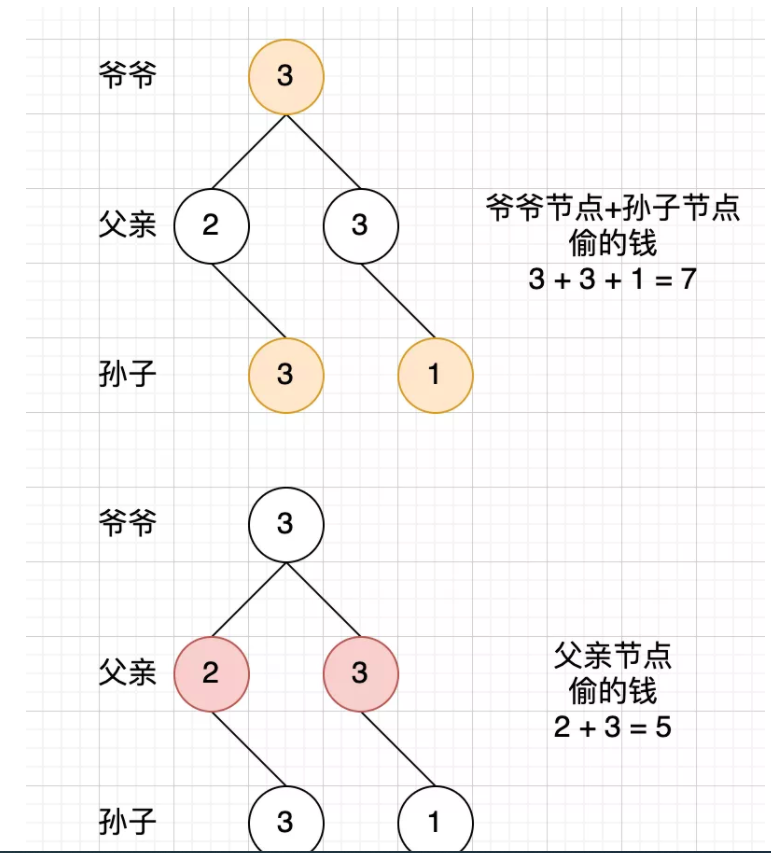
首先来定义这个问题的状态 爷爷节点获取到最大的偷取的钱数呢？

1. 首先要明确相邻的节点不能偷，也就是爷爷选择偷，儿子就不能偷了，但是孙子可以偷
2. 二叉树只有左右两个孩子，一个爷爷最多 2 个儿子，4 个孙子

根据以上条件，我们可以得出单个节点的钱该怎么算4 个孙子偷的钱 + 爷爷的钱 VS 两个儿子偷的钱，哪个组合钱多，就当做当前节点能偷的最大钱数。这就是动态规划里面的最优子结构

（可能有缜密的人想到父亲节点（如上图中的2）➕孙子节点（如上图中的1）岂不是漏了？事实上是没有的，因为另外两个孙子偷钱的情况已经包含在另外一个儿子中了）

由于是二叉树，这里可以选择计算所有子节点

• 爷爷偷的钱加上4 个孙子偷的钱如下int method1 = root.val + rob(root.left.left) + rob(root.left.right) + rob(root.right.left) + rob(root.right.right)
• 两个儿子偷的钱如下int method2 = rob(root.left) + rob(root.right);
• 挑选一个钱数多的方案则int result = Math.max(method1, method2);

  //go
  /**
   * Definition for a binary tree node.
   * type TreeNode struct {
   *     Val int
   *     Left *TreeNode
   *     Right *TreeNode
   * }
   */
  func rob(root *TreeNode) int {
   if root == nil {
    return 0
   }
      money := root.Val // money：记录爷爷➕孙子偷的钱
   if root.Left != nil {
    money += rob(root.Left.Left) + rob(root.Left.Right)
   }
   if root.Right != nil {
    money += rob(root.Right.Left) + rob(root.Right.Right)
   }
      // 返回结果为 Max（爷爷加孙子节点，父亲节点）
   return Max(money, rob(root.Left)+ rob(root.Right))
  }
  
  func Max(x, y int) int {
   if x > y {
    return x
   }
   return y
  }

方法二：状压DP

为了不当被60%击败的人，我选择一往无前！

拿出终极杀器——状压DP（状态压缩动态规划）

我们换一种办法来定义此问题

每个节点可选择偷或者不偷两种状态，根据题目意思，相连节点不能一起偷

• 当前节点选择不偷时，两个孩子节点只需要拿最多的钱出来就行(两个孩子节点偷不偷没关系)
• 当前节点选择偷时，那么两个孩子节点就不能选择偷了

我们只使用一个大小为 2 的数组来表示 res := make([]int, 2) 0 代表不偷，1 代表偷

任何一个节点能偷到的最大钱的状态可以定义为

• 当前节点选择不偷：当前节点能偷到的最大钱数 = 左孩子能偷到的钱 + 右孩子能偷到的钱
• 当前节点选择偷：当前节点能偷到的最大钱数 =  当前节点的钱数 + 左孩子选择自己不偷时能得到的钱 + 右孩子选择不偷时能得到的钱

表示为公式如下

//当前节点选择不偷：当前节点能偷到的最大钱数 = 左孩子能偷到的钱 + 右孩子能偷到的钱
res[0] = Max(left[0],left[1]) + Max(right[0],right[1])
//当前节点选择偷：当前节点能偷到的最大钱数 =  当前节点的钱数 + 左孩子选择自己不偷时能得到的钱 + 右孩子选择不偷时能得到的钱
res[1] = root.Val + left+[0] + right[0]

　　

//go 
func rob(root *TreeNode) int {
 res := robInternal(root)
 // 0表示当前节点不偷，1表示当前节点偷
 return Max(res[0],res[1])
}

func robInternal(root *TreeNode) []int {
 if root == nil {
  return []int{0, 0}
 }
 res := make([]int, 2)
 left := robInternal(root.Left)
 right := robInternal(root.Right)

 //当前节点选择不偷：当前节点能偷到的最大钱数 = 左孩子能偷到的钱 + 右孩子能偷到的钱
 res[0] = Max(left[0],left[1]) + Max(right[0],right[1])
 //当前节点选择偷：当前节点能偷到的最大钱数 =  当前节点的钱数 + 左孩子选择自己不偷时能得到的钱 + 右孩子选择不偷时能得到的钱
 res[1] = root.Val + left+[0] + right[0]

 return res
}

　　地址：https://mp.weixin.qq.com/s/u4U3c1gi5htuhou-Hxu1Hg