机器学习分类算法之逻辑回归

一、概念

逻辑回归(Logistic Regression,LR)是一种广义的线性回归分析模型,属于监督学习算法，需要打标数据，可以用在回归、二分类和多分类等问题上,最常用的是二分类。

线性回归就是通过一条曲线区分不同的数据集，在二分类问题上会有一条直线对其进行区分，如下：

逻辑回归需要每组数据都是都是数值型的，因为需要对其进行运算，得到直线系数，打标数据一般是0和1。

二、计算

逻辑回归的输出是一组特征系数，使用了 y=wx+b这种函数来进行线性拟合，这个问题的y值不是0，就是1。使用上述函数很难快速逼近0-1。为了解决这个问题，我们给出一个激活函数Sigmoid函数：

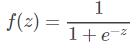
他在z趋向于无穷小时，逼近于0 ，在t趋向于无穷大时逼近于1。

让 ，函数就变为了：

而，这样，W的存在就将原本的数据集转换为了一组值在0-1之间的数，我们通过调整W的值，尽可能让数据集的值贴近目标值，即0和1。

由上面介绍可知，y=0.5时刚好是x=0；

y越趋近于0，x越小，且为负数，到负无穷时为0；

反之，y越趋近于1，x越大，且为正数，到正无穷时为1。

逻辑回归会算出一组系数，使样本的值向目标值0或1趋近，越接近目标值越好，预测就会越准确。

这里用梯度下降法来实现逻辑回归。

梯度下降法(Gradient Descent)就是每一次迭代都向目标结果接近一点，直到计算收敛。

梯度下降法的基本思想可以类比为一个下山的过程，以当前的所处的位置为基准，寻找这个位置最陡峭的地方，然后朝着山的高度下降的地方走，同理，如果我们的目标是上山，也就是爬到山顶，那么此时应该是朝着最陡峭的方向往上走。然后每走一段距离，都反复采用同一个方法，最后就能成功的抵达山谷。

梯度下降公式为：

其中是权重系数每次需要调整的值，

alpha被称之为步长，也叫乘积系数，是为了限制每次调整的大小，调整太大会错过关键信息，调整太小会迭代次数过多，所以要反复调整，

error被称之为梯度，error = sigmoid(XW) - Y，Y是目标列，

我们一般会指定一个初始特征系数，一般设为全是1，即 W=(1,1,1.....,1)，

常数项我们作为增广向量添加到数据集中，增广向量我们全部设为1，同样的，目标列也增加一个1，

最后我们还有设置一个阈值，来作为预测结果的依据，根据上面的描述，梯度下降法可选用sigmoid(XW)和0.5的比较来判断，因为小于0.5，x为负，趋近于0，大于0.5，x为正，趋近于1。

三、实现

# !/usr/bin/env python
# -*- coding: utf-8 -*-
import numpy as np
import matplotlib.pyplot as plt


def sigmoid(x):
    return 1.0 / (1 + np.exp(-x))


def grad_ascent(data_mat, class_label, alpha):
    data_matrix = np.mat(data_mat)
    label_mat = np.mat(class_label).transpose()
    m, n = np.shape(data_matrix)
    data_matrix = augment(data_matrix)  # 增广
    n += 1
    weight = np.ones((n, 1))
    while True:
        error = sigmoid(data_matrix * weight) - label_mat
        cha = alpha * data_matrix.transpose() * error
        if np.abs(np.sum(cha)) < 0.0001:
            break
        weight = weight - cha
    return weight


def create_sample():
    np.random.seed(10)  # 随机数种子，保证随机数生成的顺序一样
    n_dim = 2
    num = 100
    a = 3 + 5 * np.random.randn(num, n_dim)
    b = 18 + 4 * np.random.randn(num, n_dim)
    data_mat = np.concatenate((a, b))
    ay = np.zeros(num)
    by = np.ones(num)
    label = np.concatenate((ay, by))
    return {'data_mat': data_mat, 'label': label}


def plot_data(samples, plot_type='o'):
    data_mat = samples['data_mat']
    label = samples['label']
    n = data_mat.shape[0]
    cs = ['r', 'g']
    dd = np.arange(n)
    for i in range(2):
        index = label == i
        xx = data_mat[dd[index]]
        plt.plot(xx[:, 0], xx[:, 1], plot_type, markerfacecolor=cs[i], markersize=14)


def augment(data_matrix):
    n, n_dim = data_matrix.shape
    a = np.mat(np.ones((n, 1)))
    return np.concatenate((data_matrix, a), axis=1)


def classify(data_mat, weight):
    data_matrix = np.mat(data_mat)
    data_matrix = augment(data_matrix)
    d = sigmoid(data_matrix * weight)
    print(d)
    r = np.zeros((data_matrix.shape[0], 1))
    r[d > 0.5] = 1
    return r


def plot(weight, data):
    lx = [0, -weight[2] / weight[0]]
    ly = [-weight[2] / weight[1], 0]
    plot_data(data)
    plt.plot(lx, ly)
    plt.show()


def main():
    data = create_sample()
    final_weight = grad_ascent(data['data_mat'], data['label'], 0.001)
    print(final_weight)
    plot(final_weight, data)
    pred = classify(data['data_mat'], final_weight)
    label = np.mat(data['label']).T
    diff = np.sum(pred != label)
    print(diff, len(label), 1.0 * diff / len(label))


if __name__ == '__main__':
    main()

四、结果：

weight：

[[ 0.3236568 ]
[ 0.30234029]
[-7.00232679]]

  图形：

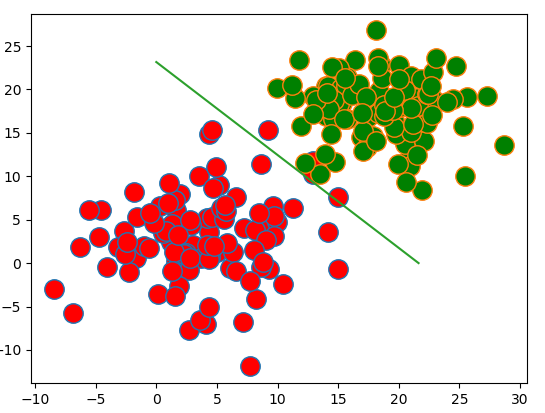
准确率：

预测不一致：4个

总数：200个

错误率：2%

调整迭代跳出条件为np.abs(np.sum(cha)) < 0.00001，则：

weight：

[[ 1.52741071]
[ 1.08976556]
[-32.00925101]]

 图形：

 

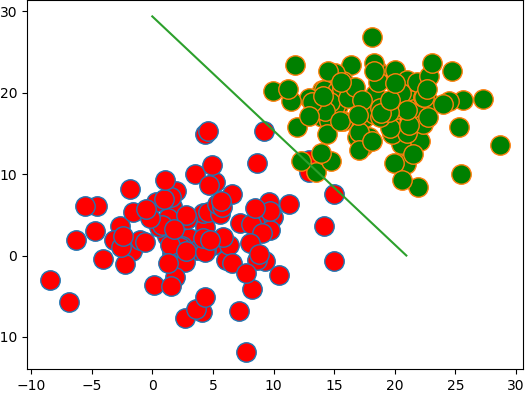
准确率：

预测不一致：3个

总数：200个

错误率：1.5%