机器学习之数据预处理

一、采样

1、随机采样

随机从样本中抽取特定数量的样本，取完放回再取叫放回采样，取完不放回叫无放回采样。

import random

def no_return_sample(data_mat, number):
    return random.sample(data_mat, number)

def return_sample(data_mat, number):
    ret = []
    for i in range(number):
        ret.append(data_mat[random.randint(0, len(data_mat) - 1)])
    return ret

if __name__ == '__main__':
    data = [[1, 2, 3], [4, 5, 6], [7, 8, 9], [2, 3, 4], [6, 7, 8]]
    print(no_return_sample(data, 3))
    print(return_sample(data, 3))
    # ret:
    # [[2, 3, 4], [4, 5, 6], [6, 7, 8]]
    # [[6, 7, 8], [6, 7, 8], [1, 2, 3]]

2、系统采样

一般采样无放回采样，将数据样本按一定规则分为n等份，再从每等份随机抽取m个样本

import random

def system_sample(data_set, number):
    k = int(len(data_set) / number)
    ret = []
    i = random.randint(0, k)
    j = 0
    while len(ret) < number:
        ret.append(data_set[i + j * k])
        j += 1
    return ret

if __name__ == '__main__':
    data = [[1, 2, 3], [4, 5, 6], [7, 8, 9], [2, 3, 4], [6, 7, 8], [9, 0, 8]]
    print(system_sample(data, 3))
    # ret:
    # [[4, 5, 6], [2, 3, 4], [9, 0, 8]]

3、分层采样

将数据分为若干个类别，每层抽取一定量的样本，再将样本组合起来

def stratified_smaple(data_set, data_set_1, data_set_2, number):
    num = int(number / 3)
    sample = []
    sample.extend(return_sample(data_set, num))
    sample.extend(return_sample(data_set_1, num))
    sample.extend(return_sample(data_set_2, num))
    return sample

if __name__ == '__main__':
    data1 = [[1, 2, 3], [4, 5, 6]]
    data2 = [[7, 8, 9], [2, 3, 4]]
    data3 = [[6, 7, 8], [9, 0, 8]]
    print(stratified_smaple(data1, data2, data3, 3))
    # ret:
    # [[4, 5, 6], [2, 3, 4], [9, 0, 8]]

二、归一化

是指将数据经过处理之后限定到一定范围，以加快收敛速度，归一化计算公式 y = (x - min_value) / (max_value - min_value)

import numpy as np


def normalize(data_set):
    shape = np.shape(np.mat(data_set))
    n, m = shape[0], shape[1]
    max_num = [0] * m
    min_num = [9999999999] * m
    for data_row in data_set:
        for index in range(m):
            if data_row[index] > max_num[index]:
                max_num[index] = data_row[index]
            if data_row[index] < min_num[index]:
                min_num[index] = data_row[index]
    section = list(map(lambda x: x[0] - x[1], zip(max_num, min_num)))
    data_mat_ret = []
    for data_row in data_set:
        distance = list(map(lambda x: x[0] - x[1], zip(data_row, min_num)))
        values = list(map(lambda x: x[0] / x[1], zip(distance, section)))
        data_mat_ret.append(values)
    return data_mat_ret

三、去除噪声

去噪即指去除数据样本中有干扰的数据，噪声会大大影响速率的收敛速率，也会影响模型的准确率；

因为大多数随机变量的分布均按正态分布，正太分布公式

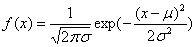
δ代表数据集方差，μ代表数据集均值，x代表数据集数据，正太分布的特点，x落在（μ-3δ，μ+3δ)外的概率小于三千分之一，可以认为是噪声数据。

from __future__ import division
import numpy as np


def get_average(data_mat):
    shape = np.shape(data_mat)
    n, m = shape[0], shape[1]
    num = np.mat(np.zeros((1, m)))
    for data_row in data_mat:
        num = data_row + num
    num = num / n
    return num


def get_variance(average, data_mat):
    shape = np.shape(data_mat)
    n, m = shape[0], shape[1]
    num = np.mat(np.zeros((1, m)))
    diff = data_mat - average
    square = np.multiply(diff, diff)
    for data_row in square:
        num = data_row + num
    num = num / n
    return np.sqrt(num)


def clear_noise(data_set):
    data_mat = np.mat(data_set)
    average = get_average(data_mat)
    variance = get_variance(average, data_mat)
    data_range_min = average - 3 * variance
    data_range_max = average + 3 * variance
    noise = []
    for data_row in data_mat:
        if (data_row > data_range_max).any() or (data_row < data_range_min).any():
            noise.append(data_row)
    print(noise)


data1 = [[2, 3, 4], [4, 5, 6], [1, 2, 3], [1, 2, 1], [1000, 1000, 1], [1, 2, 1], [1, 2, 1], [1, 2, 1], [1, 2, 1],
         [1, 1, 1], [1, 2, 2], [2, 2, 1]]
clear_noise(data1)
# ret:
# [matrix([[1000, 1000,    1]])]

四、数据过滤

在数据样本中，可能某个字段对于整个数据集没有什么意义，影响很小，那么就可以把它过滤掉，比如用户id对于判断产品整体购买与未购买数量及趋势就意义不大，带入算法前，直接过滤掉就可以。