一、 实验目的
理解有向图的基本概念,掌握有向图的存储结构,实现有向图的拓扑排序和关键路径算法.
二、 实验内容
通过编写程序,对示例图进行拓扑排序,进而求解示例图的关键路径。
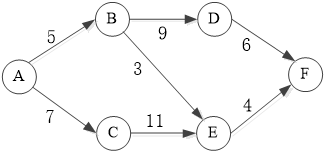
具体步骤如下:
- 构造有向带权图;
- 定义拓扑排序函数判断图中是否存在回路;
- 定义关键路径求解函数;
- 主函数实现数据的输入及函数调用。
三、 实验工具
Dev - C++
四、 实验代码
//Authors:xiaobei
#include<stdio.h>
#include<stdlib.h>
#define MVNum 100
#define OK 1
#define ERROR 0
int topo[MVNum]; //定义拓扑排序数组
//邻接表结构的相关定义
typedef struct ArcNode{ //边表
int adjvex;//该边所指向的顶点位置
struct ArcNode *nextarc;//指向下一条边的指针
char info; //和边相关信息,权值
}ArcNode;
typedef struct VNode{ //表头结点表
char data;
ArcNode *firstarc;
}VNode,AdjList[MVNum];
typedef struct{ //邻接表,带权有向图
AdjList vertices;
int vexnum,arcnum;
}ALGraph;
//链栈的相关定义
typedef struct StackLink{
int data;
struct StackLink *next;
}StackLink,*StackNode;
int InitStack(StackNode &S){
S = NULL;
return OK;
}
int Push(StackNode &S,int e){
StackNode p;
p = (StackLink*)malloc(sizeof(StackLink));
p->data = e;
p->next = S;
S = p;
return OK;
}
int Pop(StackNode &S,int &e){
StackNode p;
p = (StackLink*)malloc(sizeof(StackLink));
if(S==NULL)
return ERROR;
e = S->data;
p = S; //用P临时存放栈顶元素,已备释放
S = S->next;
free(p);
return OK;
}
int GetTop(StackNode S){
if(S!=NULL)
return S->data;
}
int StackEmpty(StackNode S){
if(S!=NULL)
return ERROR;
else
return OK;
}
//函数返回顶点所在位置
int LocateVex(ALGraph G,char c){
int i;
for(i=0;i<G.vexnum;++i){
if(c==G.vertices[i].data)
return i;
}
return -1;
}
//函数用邻接表创建有向无环图
int CreateDAG(ALGraph &G){
int i,j,k,weight;
char v1,v2;
ArcNode* p;
printf("
[请输入总顶点与总边数]:
>>>");
scanf("%d %d",&G.vexnum,&G.arcnum);
for(i=0;i<G.vexnum;i++){ //输入各点,构造表头结点表
printf("
[请依次输入顶点信息]:
>>>");
getchar();
scanf("%c",&G.vertices[i].data);
G.vertices[i].firstarc = NULL;
}
for(k=0;k<G.arcnum;k++){
printf("
[请输入各边及权值构造邻接表]:
>>>");
getchar();
scanf("%c %c %d",&v1,&v2,&weight);
i = LocateVex(G,v1);
j = LocateVex(G,v2);
p = (ArcNode*)malloc(sizeof(ArcNode));
p->adjvex = j;
p->info = weight;
p->nextarc = G.vertices[i].firstarc;
G.vertices[i].firstarc = p;
}
return OK;
}
//函数求出每个顶点入度存入数组 indegree[]
void FindInDegree(ALGraph G,int indegree[]){
//求有向图邻接表顶点入度,两种方法:1、建立逆邻接表,2、遍历整个邻接表
//这里采用遍历整个邻接表
ArcNode *p;
int i;
for(i=0;i<G.vexnum;i++) //入度初始化为零
indegree[i] = 0;
for(i=0;i<G.vexnum;i++){ //遍历邻接表
p = G.vertices[i].firstarc;
while(p!=NULL){
indegree[p->adjvex]++;
p = p->nextarc;
}
}
}
//函数获得拓扑排序结果数组topo[]
int TopologicalSort(ALGraph G,int topo[]){
//有向图G采用邻接表存储结构
//若G无回路,则生成G的一个拓扑序列topo[]并返回OK,否则返回ERROR
int i;
ArcNode *p;
StackNode S; //定义链栈
int indegree[MVNum];
FindInDegree(G,indegree); //求出各顶点入度,存入数组indegree中
printf("各顶点入度:");
printf("
-----indegree-----
");
for(i=0;i<G.vexnum;i++){
printf("%d",indegree[i]);
}
printf("
-----indegree-----
");
InitStack(S); //栈初始化为空
for(i=0;i<G.vexnum;i++){
if(indegree[i]==0)
Push(S,i); //入度为零者入栈
}
int m=0;
while(!StackEmpty(S)){
Pop(S,i); //将栈顶顶点vi出栈
topo[m] = i; //将vi保存在拓扑序列数组topo中
m++; //对输出顶点计数
p=G.vertices[i].firstarc; //p指向第一个邻接点
while(p!=NULL){
int k = p->adjvex; //vk为vi的邻接点
indegree[k]--; //vi的每个邻接点入度减1
if(indegree[k]==0)
Push(S,k); //若入度为0则入栈
p = p->nextarc; //p指向vi的下一个邻接点
}
}
if(m<G.vexnum) //判断有无回路
return ERROR;
else
return OK;
}
int CriticalPath(ALGraph G){
//G为邻接表存储的有向网,输出G的各项关键活动
ArcNode *p;
int ve[MVNum]; //ve[MVNum]记录每个事件最早发生时间
int vl[MVNum]; //vl[MVNum]记录每个事件最迟发生时间
int i,j,k,e,l;
if(!TopologicalSort(G,topo))
return ERROR; //调用拓扑排序算法,使拓扑序列保存在topo中;若调用失败,则存在有向环,返回ERROR
int n = G.vexnum; //n为顶点个数
for(i=0;i<n;i++)
ve[i] = 0; //个每个事件的最早发生时间置初值0
/*-----------------按拓扑次序求每个事件最早发生时间-----------------*/
for(i=0;i<n;i++){
k=topo[i]; //取得拓扑排序序列中顶点序号k
p = G.vertices[k].firstarc; //p指向k的第一个邻接顶点
while(p!=NULL){ //依次更新k的所有邻接顶点的最早发生时间
j = p->adjvex; //j为邻接顶点的序号
if(ve[j]<ve[k]+p->info) //更新顶点j的最早发生时间ve[j]
ve[j] = ve[k]+p->info;
p = p->nextarc; //p指向k的下一个邻接顶点
}
}
for(i=0;i<n;i++) //给每个事件的最迟发生时间置初值ve[n-1]
vl[i] = ve[n-1];
/*-----------------按逆拓扑次序求每个事件最迟发生时间-----------------*/
for(i=n-1;i>=0;i--){
k = topo[i]; //取得拓扑排序序列中顶点序号k
p = G.vertices[k].firstarc; //p指向k的第一个邻接顶点
while(p!=NULL){ //根据k的邻接点,更新k的最迟发生时间
j = p->adjvex; //j为邻接顶点的序号
if(vl[k]>vl[j]-p->info) //更新顶点k的最早发生时间vl[k]
vl[k] = vl[j]-p->info;
p = p->nextarc; //p指向k的下一个邻接顶点
}
}
/*-----------------判断每一活动是否为关键活动-----------------*/
printf("关键路径如下:
");
for(i=0;i<n;i++){
p = G.vertices[i].firstarc; //p指向k的第一个邻接顶点
while(p!=NULL){
j = p->adjvex; //j为i的邻接顶点的序号
e = ve[i]; //计算活动<vi,vj>的最早开始时间
l = vl[j]-p->info; //计算活动<vi,vj>的最迟开始时间
if(e==l) //若为关键活动则输出<vi,vj>
printf("<%c,%c>",G.vertices[i].data,G.vertices[j].data);
p = p->nextarc; //p指向i的下一个邻接顶点
}
}
printf(" ->end
");
return OK;
}
//菜单函数
void Menu(){
printf("
---------菜单-------
");
printf("
1、创建图结构
");
printf("
2、拓扑排序
");
printf("
3、计算关键路径
");
printf("
0、退出
");
printf("
--------------------
");
printf("
[请输入你的选择:]
>>>");
}
//主函数
int main(){
int i,user;
ALGraph G;
while(true){
Menu();
scanf("%d",&user);
switch(user){
case 1:{
if(CreateDAG(G))
printf("
创建成功……
");
break;
}
case 2:{
if(TopologicalSort(G,topo)){
printf("拓扑排序结果如下:
");
for(i=0;i<G.vexnum;i++)
printf("%c->",G.vertices[topo[i]].data);
printf("end
");
}
break;
}
case 3:{
CriticalPath(G);
break;
}
case 0:exit(0);
}
}
return 0;
}五、实验结果
1. 创建图结构


2. 拓扑排序
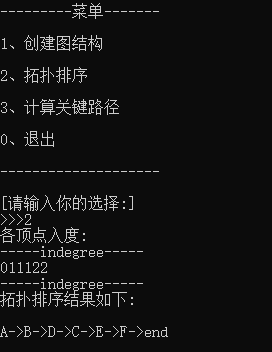
3.关键路径

4.退出
六、总结与思考
1. 用顶点表示活动,用弧表示顶点间的优先关系的有向图,称为顶点表示活动的网,简称(Activity On Vertex Network)AOV-网;
2. 所谓拓扑排序,就是将AOV-网中的所有顶点排成一个线性序列,该序列满足:若在AOV-网中由顶点vi到顶点vj有一条路径,则在该线性序列中,顶点vi必在vj之前;
3. 拓扑排序的过程,重复选择没有直接前驱的顶点;
4. 与AOV-网相对,AOE-网是以边表示活动的网。AOE-网是一个带权的有向无环图。顶点表示事件,弧表示活动,权表示活动持续时间。
5. AOE-网在工程计划和经营管理中通常需要解决以下两个问题:
1)估算完成整项工程至少需要多长时间;
2)判断哪些活动是影响工程进度的关键;
6. 源点、汇点、关键活动、关键路径
7. 一个活动的最迟开始时间l(i)与最早开始时间e(i)的差值l(i)-e(i)是该活动完成的时间余量,它是在不增加完成整个工程所需总时间的情况下,活动ai可以拖延的时间,当一个活动时间余量为零时,说明该活动必须如期完成,否则会拖延整个工程进度。所以称l(i)-e(i)=0,即l(i)=e(i)的活动为关键活动。