我们先来看一张图
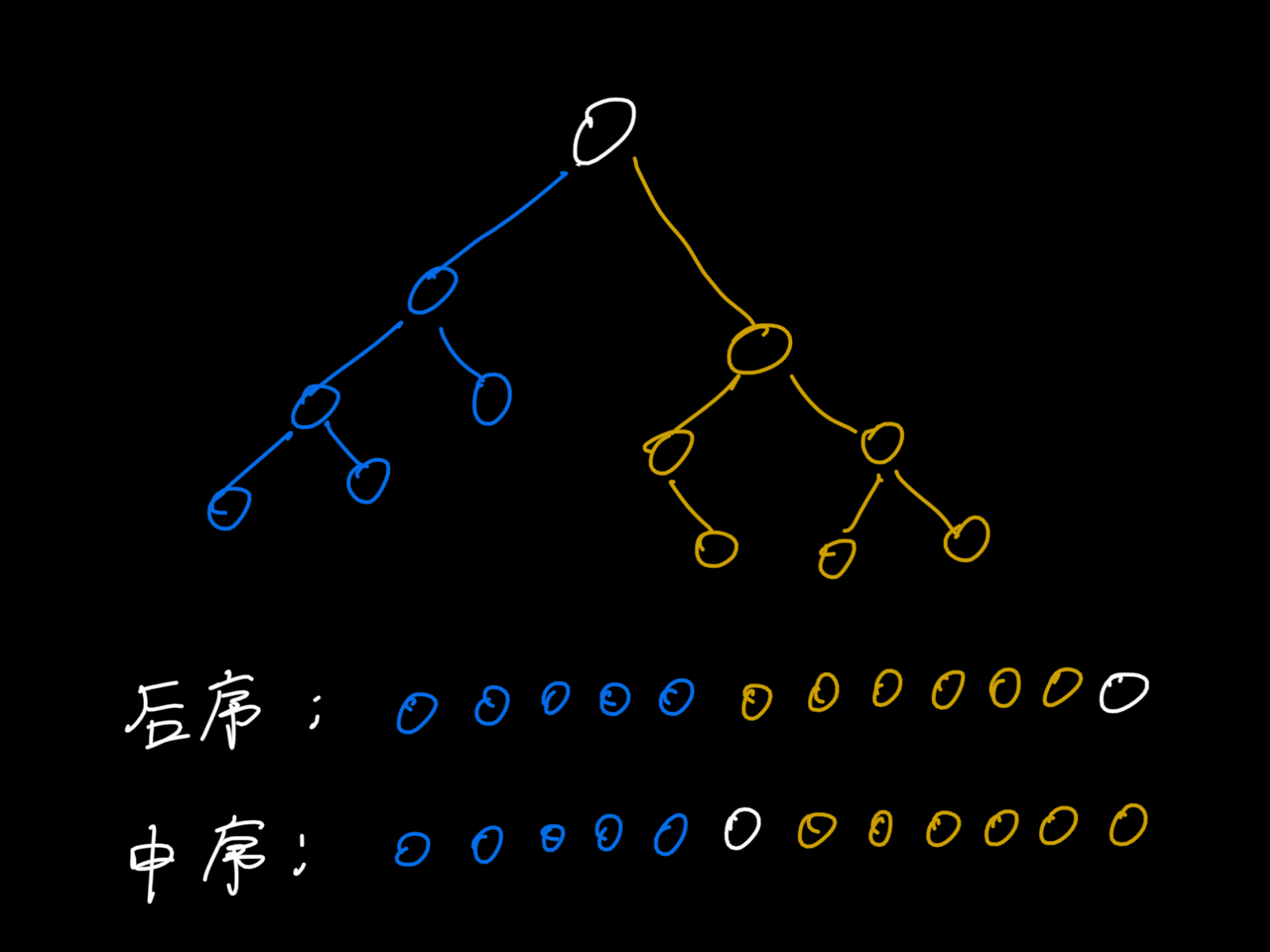
- 这里我们只关注 中序和后序遍历 对于对应子树的 根节点及其左子树和右子树 的划分。
可以看到中序遍历的整体情况是左子树根右子树,
而后序遍历则是左子树右子树根。
从中我们可以了解到第一个性质:一颗树的后序遍历的最后一个节点一定是当前树的根。
我们利用这个性质就可以找到当前子树的根了,那么对于子树的前序和后续遍历序列我们又该如何处理?
- 别急,继续观察前序和后序遍历的序列,我们还可以发现第二个性质
对一棵树进行中序和后序遍历产生的序列,
其左子树和右子树在对应序列中的分布都是是连续的
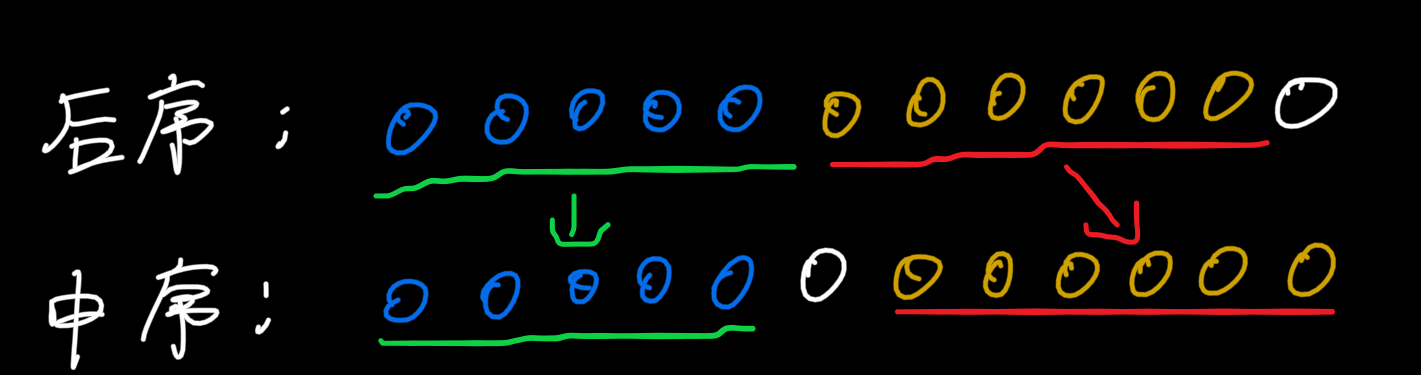
这个性质将是接下来可以独立操作各子树的关键
-
接下来,我们将左右两颗子树拿下来分别当成独立的一棵树来看(相应的后序与中序遍历序列与第一张图对应)
左子树 和 右子树
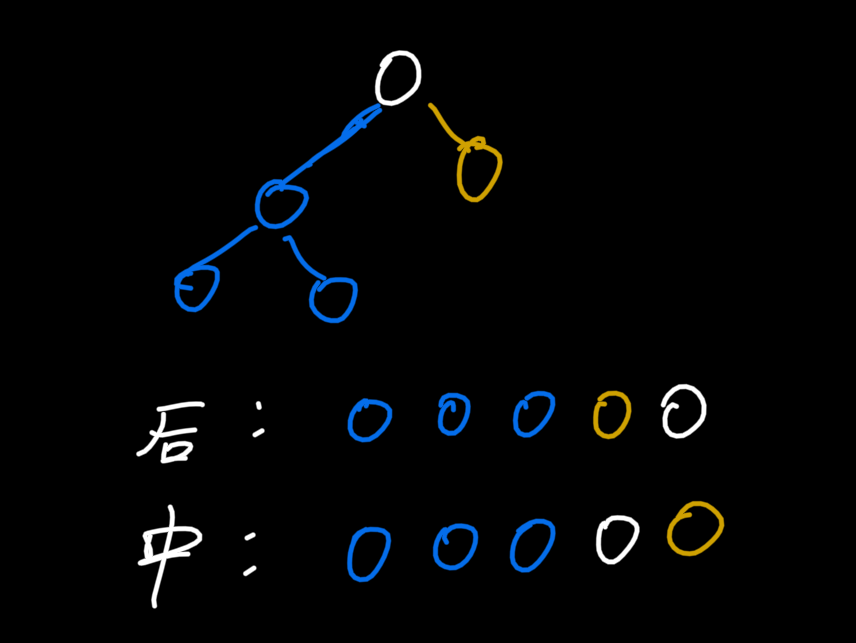

-
可以发现我们之前发现的两个性质对于一棵树的子树也是同样适用的(树是递归定义的),那么在我们找完一颗树的根节点后,想要得到前序遍历的结果,只需要在对树进行中序和后序遍历产生的序列中分别找到其
左子树和右子树的部分继续递归查找即可。
由此我们可以大概得出这样一个流程
我们先将该子树在中序遍历序列中的范围表示为
[left(左端点), right(右端点)]
在后续遍历序列中最后一个元素的位置用last表示。
- 输出该树(子树)的后序遍历的最后一个元素(即该树(子树)的根节点)
下面的描述将省略主体 -- 当前子树 - 找到后续遍历的最后一个元素(即根节点)在对应中序遍历序列中的位置(记为pov),则对应左右子树在中序遍历序列中的范围为
[left, pov - 1]和[pov + 1, right] - 分别在后续遍历序列中找到左子树的last,记为
l_last, 右子树的last, 记为r_last - 将左右子树当成独立的树看待(性质二的区间连续保证了可以这样做),将找到的左右子树在中序和后序遍历序列中的范围和位置作为各自的参数重复执行第一步。
- 在第三步中右子树的
r_last显然是last - 1。
左子树的l_last经过观察可以发现,它的位置距离相对last(此处非左子树的l_last)隔了一个右子树的大小
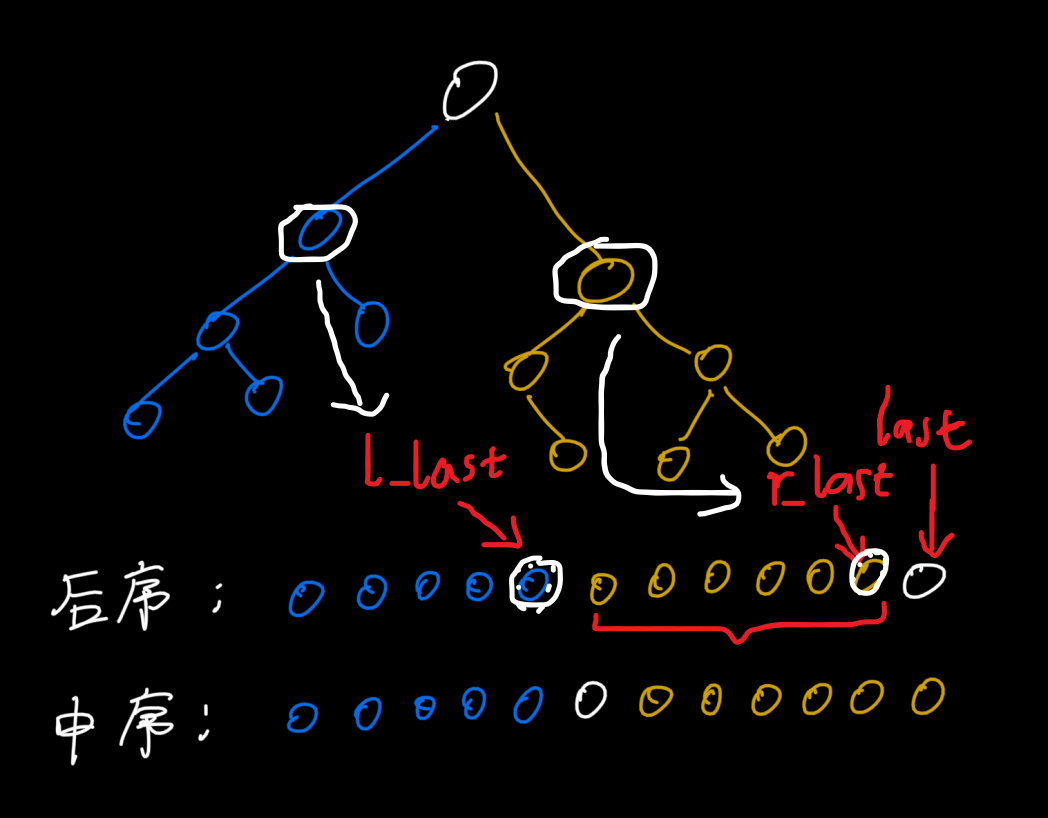
因此 l_last 的位置就是 last - 右子树大小 - 1 --> last - (right - (pov + 1) + 1) - 1 = last - right + pov - 1
接下来就是代码实现拉~~~
#include<iostream>
#include<algorithm>
#include<cstring>
#include<unordered_map>
using namespace std;
const int N = 50;
unordered_map<int, int> m;
int flect[N], hash_idx = 0;
int hash_(int x){
//因为题目给出的树的节点编号不一定连续所以做了下离散化
if(!m[x]){
m[x] = ++hash_idx;
flect[hash_idx] = x;
}
return m[x];
}
int mid[N], post[N];
int flectmid[N];//对应的值在中序遍历序列中的位置
// l, r 当前子树在mid数组中的范围
// p 当前子树的根节点在post数组中的位置
void dfs(int l, int r, int p){
if(l > r || p <= 0) return;
printf(" %d", flect[post[p]]);
int pov = flectmid[post[p]];
//左子树
dfs(l, pov - 1, p - (r - pov + 1));
//右子树
dfs(pov + 1, r, p - 1);
}
int main(){
int n;
scanf("%d", &n);
for(int i = 1; i <= n; i++){
scanf("%d", post + i);
post[i] = hash_(post[i]);
}
for(int i = 1; i <= n; i++){
scanf("%d", mid + i);
mid[i] = hash_(mid[i]);
flectmid[mid[i]] = i;
}
printf("Preorder:");
dfs(1, n, n);
}