EM算法

EM算法是一种迭代算法，用于含有隐变量的概率模型参数的极大似然估计，或极大后验概率估计。EM算法的每次迭代分两步：E步，求期望（Expectation）；M步，求极大（Maximization）。

EM算法

这里也直接给出书上的例子，让还不了解的读者先上车...哦错了，先感受。不过这里阐述会简单些。

（三硬币模型）假设有A,B,C三枚硬币，正面出现的概率分别为π,p,q。一次试验为：先抛A，如果出现正面则选择B，否则选择C，然后再抛选出的硬币，记录抛此枚硬币的结果，正面向上为1，反面向上为0。独立重复试验10次，观测结果为：

1,1,0,1,0,0,1,0,1,1

只能观测到上面这个结果，不能观测选择的是B还是C。设随机变量y表示观测变量，表示一次试验的观测结果为1或者0，随机变量z是隐变量表示抛A的结果，或者说选择的是B还是C，θ=(π,p,q)是模型参数，于是一次试验中观测结果为y的概率为

   (1)

右端第一项对应z=1，第二项对应z=0

假设观测数据为Y=(Y₁,Y₂,...,Y_n)，不可观测数据为Z=(Z₁,Z₂,...Z_n)，则观测数据的似然函数为

                        (2)

由于是独立重复试验（n次），则

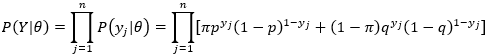          (3)

模型参数θ=(π,p,q)的极大似然估计

                     (4)

然而上式没有解析解，只能通过迭代的方法求数值解，比如这里的EM算法。

算法

选取模型参数θ=(π,p,q)的初值，记作

θ₀=(π₀,p₀,q₀)

然后通过某种迭代更新参数，直至算法收敛。

第i次迭代参数的估计值记作

θ_i=(π_i,p_i,q_i)

第i+1次迭代方式如下，

E步：计算观测数据y_j来自硬币B（z=1）的概率

     (5)

其中，分母为出现y_j观测结果的概率（来自硬币B和来自硬币C的概率之和），分子是y_j观测结果来自硬币B的概率。

顺便一提，y_j来自硬币C的概率自然就是1-μ_i+1(y_j)

M步：计算模型参数新估计值

             (6)

          (7)

    (8)

其实，A出现正面的概率π就是观测数据来自硬币B的概率，(6)是取了样本平均。(7)式中分母其实等于 nπ_i+1，此即n次试验中选择硬币B的次数，而分子则是n次试验中选择硬币B并且抛掷B出现正面的次数，从而得到硬币B的正面出现概率。类似的(8)则是计算硬币C出现正面的概率。y_j表示第j次试验中的观测结果（为1或者0）。

于是，我们假设参数初值为

π₀=0.5,p₀=0.5,q₀=0.5

按照上述步骤进行迭代计算，直至收敛（每个参数均不再变化，或者每个参数的变化分别低于一个设定的阈值或者||θ_i+1-θ_i||小于一个设定的阈值），这里省去具体过程，得到结果为

θ=(0.5,0.6,0.6)

如果初值为

π₀=0.4,p₀=0.6,q₀=0.7

迭代结果为

θ=(0.4064,0.5368,0.6432)

 可见，不同的初值会导致不同的迭代结果。

 假设观测数据Y，概率分布为P(Y|θ)，其中θ为需要估计的模型参数，则，不完全数据Y的似然函数为P(Y|θ)，对数似然函数为logP(Y|θ)。假设Y和隐随机变量Z的联合概率分布为P(Y,Z|θ)，那么完全数据的对数似然函数为logP(Y,Z|θ)。EM算法通过迭代求L(θ)=logP(Y|θ)的极大似然估计。

Q函数

Q函数为完全数据的对数似然函数logP(Y,Z|θ)关于在给定观测数据Y和当前参数θ_i下对未观测数据Z的条件概率分布P(Z|Y,θ_i)的期望，即

     (9)

上面这个定义可能说的不是很明白，这里稍微解释一下。我们知道Y和θ_i是已知的，令L(Z)=logP(Y,Z|θ)，所以Q函数就是L(Z)在Y和θ_i下的条件期望，

   (10)

其中，P(Z|Y,θ_i)为已知Y和θ_i下的Z的条件概率，P(Y,Z|θ)为观测数据Y和隐数据Z的联合概率分布，根据(2)式，不难知道，

P(Y,Z|θ)=P(Z|θ)P(Y|Z,θ)                        (11)

而我们的目标就是logP(Y,Z|θ)（也就是L(Z)）的极大似然估计，所以对logP(Y,Z|θ)的条件期望求极大值

                  (12)

(11)式所对应的θ就是下一次迭代的θ的估计

  (13)

步骤

输入：观测变量数据Y，隐变量数据Z，联合分布P(Y,Z|θ)，条件分布 P(Z|Y,θ)

输出：模型参数θ

1. 选择初始值θ₀=(π₀,p₀,q₀)
2. E步：记θ_i为第i次迭代参数的估计值，在第i+1次迭代时，计算(10)式
3. M步：根据(13)式计算第i+1次迭代参数的估计值
4. 重复步骤2和3，直到收敛

几点说明

1. 参数的初值虽然可以任意选择，但不同的初值会影响最终的迭代结果
2. M步求Q函数的极大值，可能是局部极值（也不难理解，如果是全局极大值，那最终迭代结果就与初值的选择无关了）
3. 停止迭代的条件一般使用||θ_i+1-θ_i||<ε 或者||Q(θ_i+1, θ_i)-Q(θ_i,θ_i)||<ε, 其中 ε 是某个阈值

 ref

统计学习方法，李航