0.PTA得分截图

1.本周学习总结(0-5分)
1.1串
1.串的存储结构
(1)定长顺序存储:类似线性表顺序存储,由一组地址连续的存储单元存储
(2)堆分配存储:也由一组地址连续的存储单元,存储空间是在程序执行过程中动态分配new char[length]
(3)链式存储:一个结点可以存储一个或多个字符(通常将链串中每个结点所存储的字符个数称为结点大小),但有时操作不便
2.串的模式匹配算法
(较多应用于文本查重)
主串:目标串
子串:模式串
①BF算法(需回溯)
若主串长度为n,子串长度为m
因为其主串和子串位置指针都是需要回溯,则:
最好情况时间复杂度为O(m)而最坏情况则可达到O(n*m)

主串s
子串t//string型
while (i<s.size()&& j<t.size())
{
if (s.data[i]==t.data[j])//若当前字符匹配,则继续匹配下一个字符
{
i++;//主串和子串都需要向后移动
j++;
}
else//主串、子串指针回溯重新开始下一次匹配
{
i=i-j+1;//主串从上一次匹配开始位置的下一个位置开始匹配
j=0;//子串从头开始匹配
}
}
②kmp算法(不需回溯)
next数组
当 t[j] == t[k] 时,t[0]…t[k-1]" == " t[j-k]…t[j-1],且 t[j] == t[k],所以next[j+1]=k+1
当 t[j] == t[k] 时,t[j+1] 的最大子串的长度为 k,
当 t[j] != t[k] 时, next[j+1] < k,
那么求 next[j+1] = 求 t[j-k+1] ~ t[j] 与 t[0] ~ t[k-1] 的符合 k 的子串 = 求next[k]
int j=0,k=-1;
next[0]=-1;
while(j<t.length-1)
{
if(k == -1 || t[j] == t[k])
{
j++;k++;
next[j] = k;
}
else k = next[k];//t[j] != t[k]
}

nextval数组(当两个字符相同时,就跳过)next优化
int j=0,k=-1;
nextval[0]=-1;
while(j<t.length-1)
{
if(k == -1 || t[j] == t[k])
{
j++;k++;
if(t[j]==t[k])
nextval[j] = nextval[k];
else
nextval[j] = k;
}
else
k = nextval[k];
}
3.cin,getline,cin.getline输入字符串
①cin
cin>>
1.cin读取数据时,从第一个非空白字符(空格、制表符或换行符)开始阅读,当它读取到下一个空白字符时停止读取;
2.cin会把换行符留在输入队列中;
②getline
getline函数:
getline(cin(正在读取的输入流), inputLine(接收输入字符串的 string 变量的名称))
1.可读取整行,包括空格(若开头结尾有空格也读取),并将其存储在字符串对象中;
2.读取换行符并且将换行符替换成'�',但是会丢弃换行符(即输入队列不存在换行符);
③cin.getline
cin.getlin函数:
cin.getline(line,100)
1.类似字符数组char line[100];
2.cin.getline读取换行符并替换成'�',并且不会主动丢弃换行符,会把它留在输入队列中
1.2树
(非线性结构:一对多)
基本术语:
例:
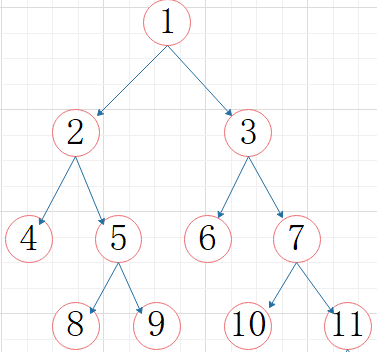
根结点:没有前驱(1)
终端(叶子)结点:没有后继(4,8,9,6,10,11)
双亲(父亲):即上层的那个结点(直接前驱)(4的父亲为2,7的父亲为3)
孩子:直接连接的下层结点(直接后继)(2的孩子为4,5)
兄弟:同双亲且同层结点(4的兄弟为5,6的兄弟为7)
祖先:从根到该结点所经分支的所有结点(8的祖先为5,2,1)
子孙:该结点任意子树(6,7,10,11都为3的子孙)
度:分支数目(子树个数)
1.3二叉树
结点特点:
①非空二叉树上叶节点数等于双分支结点数加1
n0:度为0(叶子结点),n1:度为1(单分支),n2:度为2(双分支)
总结点数=n0+n1+n2 = 分支数 + 1
分支数=n1+2*n2
所以:n0+n1+n2 = n1+2*n2+1
n0 = n2+1
②二叉树的第 i 层上至多有2(i-1)个结点
③高度为h的二叉树至多有2h-1个结点,至少有h个结点
1、特殊的二叉树
(1)满二叉树
所有分支结点都有双分结点,并且叶结点都集中在二叉树的最下一层
高度为h的满二叉树有2h-1个结点
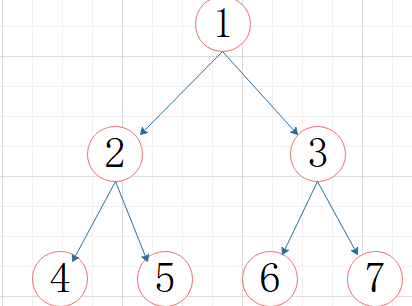
(2)完全二叉树
没有单独右分支结点
结点数:2(h-1)-1< n <=2h-1
满二叉树是完全二叉树的一个特例

特点:
①度为1节点,只可能有一个,且该结点只有左孩子无右孩子
②除树根结点外,若一个结点的编号为i,则它的双亲结点的编号为i/2
③若编号为i的结点有左或右孩子结点,左孩子结点的编号为2i右孩子结点的编号为2i+1
④若i≤n/2(取下限),则编号为i的结点为分支结点,否则为叶结点
2、二叉树存储结构
①顺序存储结构(数组存储:从上至下、从左到右)
1、非根结点i的父结点序号为i/2(取下限)
2、结点i的左孩子序号为2i
3、结点i的右孩子序号为2i+1
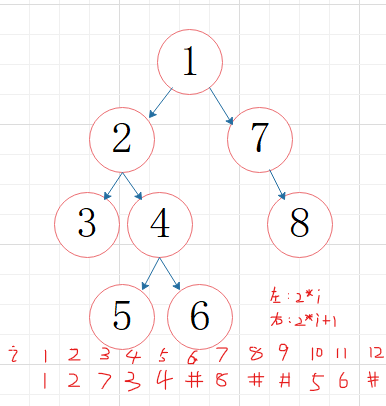
完全二叉树来说,其顺序存储是十分合适
数据较大后,空间利用率较低
数组缺点,查找、插入删除不方便
②链式存储结构
结点包含:数据域和左、右指针域
typedef struct TNode
{
ElemType data;
struct node *lchild,*rchild;
}TNode;

若一棵树n个结点
2n个指针域
非空指针域有n-1个
空指针域2n-(n-1) = n+1
3、二叉树建立
顺序存储建立二叉树
(顺序存储结构转成二叉链)

i从1开始
if (i > len - 1) return NULL;
if (str[i] == '#') return NULL;
BT = new TNode;
BT->data = str[i];
BT->lchild = CreateBtree(str, 2 * i);//左子树
BT->rchild = CreateBtree(str, 2 * i + 1);//右子树
return BT;
先序存储建立二叉树
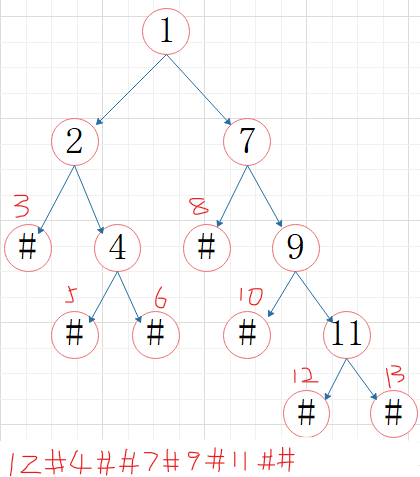
if (i > len - 1)return NULL;
if (str[i] == '#')return NULL;
BT = new TNode;
BT->Data = str[i];
BT->lchild = CreatBinTree(str, ++i);
BT->rchild = CreatBinTree(str, ++i);
return BT;
先序中序建立二叉树

if (count <= 0)
return NULL;
BT = new TNode;
BT->data = *preLine;
for (ch = inLine; ch < inLine + count; ch++)//查找先序序列当前元素在中序序列中的位置
{
if (*ch == *preLine)
break;
}
k = ch - inLine;//左子树剩余结点个数
BT->lchild = CreatTree(preLine + 1, inLine, k);
BT->rchild = CreatTree(preLine + k + 1, ch + 1, count - k - 1);
return BT;
后序中序建立二叉树
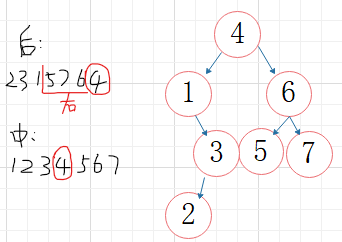
if (count <= 0)
return NULL;
BT = new TNode;
BT->data = *(postLine + count - 1);
for (ch = inLine; ch < inLine + count; ch++)//查找先序序列当前元素在中序序列中的位置
{
if (*ch == *preLine)
break;
}
k = ch - inLine;//左子树剩余结点个数
BT->lchild = CreatTree(postLine, inLine, k);
BT->rchild = CreatTree(postLine + k, num + 1, count - k - 1);
return BT;
4、二叉树遍历
1.递归遍历法
①先序遍历
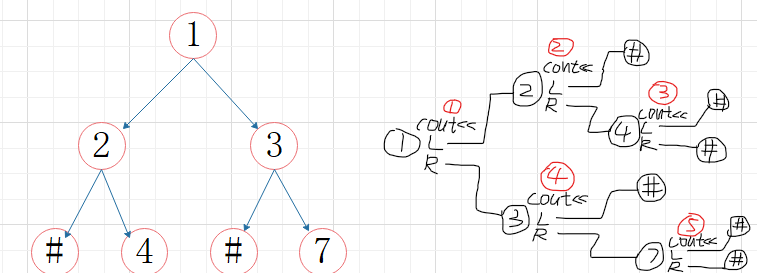
void PreOrder(BTree bt)
{ if (bt!=NULL)
{ printf("%c ",bt->data); //访问根结点
PreOrder(bt->lchild);
PreOrder(bt->rchild);
}
}
②中序遍历
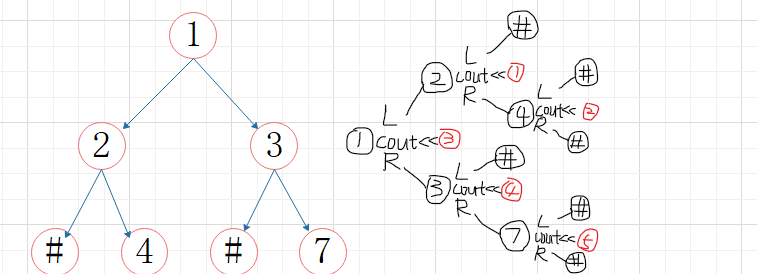
void InOrder(BTree bt)
{ if (bt!=NULL)
{ InOrder(bt->lchild);
cout<<bt->data; //访问根结点
InOrder(bt->rchild);
}
}
③后序遍历

void PostOrder(BTree bt)
{ if (bt!=NULL)
{ PostOrder(bt->lchild);
PostOrder(bt->rchild);
printf("%c ",bt->data); //访问根结点
}
}
1.非递归遍历法
①层次遍历(利用栈,先进先出)
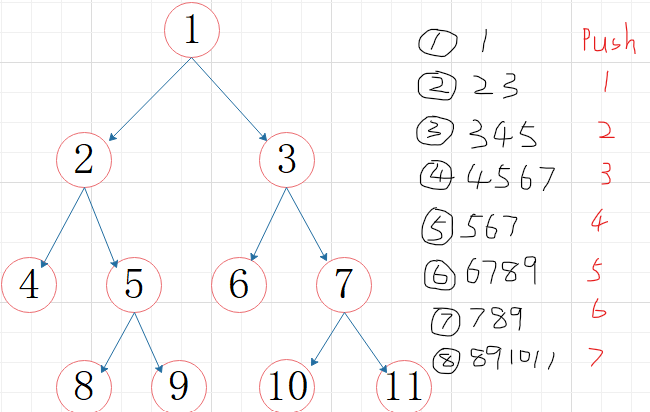
void PrintTree(BTree BT)//层次遍历二叉树
{
BTree ptr;//遍历二叉树
queue<BTree>qu;
qu.push(BT);//根结点进栈
while (!qu.empty())//若队列不为空
{
ptr = qu.front();//第一个元素出栈
qu.pop();
cout << ptr->data;
if (ptr->lchild != NULL)//若出栈元素有左右子结点,进栈
qu.push(ptr->lchild);
if (ptr->rchild != NULL)
qu.push(ptr->rchild);
}
}
5、哈夫曼树
(具有最小带权路径长度的二叉树)
二叉树的带权路径长度wpl:(若有n个带权值的叶子结点)从根结点到各个叶子结点的路径长度与相应结点权值的乘积的和
原则:
权值越大的叶结点越靠近根结点;权值越小的叶结点越远离根结点
哈夫曼树总节点数
结点总数n = n0+n1+n2
因为,哈夫曼树结点度为0或2
所以,n=n0+n2
因为,n0=n2+1
所以,总结点n = 2n0-1
哈夫曼树建树
结构体定义
typedef struct HTNode
{ char data; //结点数据
float weight; //权值
int parent;//双亲结点
int lchild;//左孩子结点
int rchild;//右孩子结点
} HTNode;
for i=0 to 2*n-1 do
初始化每个结点的值ht[i].parent=ht[i].lchild=ht[i].rchild=-1;
end for
//构造哈夫曼树
给定一组权值W
1、在W中选出权值最小ht[lnode]和次小ht[rnode]的两棵二叉树作为左、右子树构造一棵的二叉树
(新二叉树根结点的权值为其左、右子树根结点权值之和:ht[i].weight= ht[lnode].weight+ht[rnode].weight)
2、新二叉树根结点的权值放入W中,重复操作直到W为空
for (i = n; i < 2 * n - 1; i++)
{
smallest = SecSmallest = MAXNUM;
lnode = rnode = -1;
for (j = 0; j < i; j++)
{
if (HTNodes[j].parent == -1)
{
if (HTNodes[j].weight < smallest)//遍历寻找最小权值
{
SecSmallest = smallest;
rnode = lnode;
smallest = HTNodes[j].weight;
lnode = j;
}
else if (HTNodes[j].weight < SecSmallest)//遍历寻找次小权值
{
SecSmallest = HTNodes[j].weight;
rnode = j;
}
}
}
HTNodes[lnode].parent = i;
HTNodes[rnode].parent = i;
HTNodes[i].weight = HTNodes[lnode].weight + HTNodes[rnode].weight;//新二叉树根结点的权值
HTNodes[i].lchild = lnode;
HTNodes[i].rchild = rnode;
}
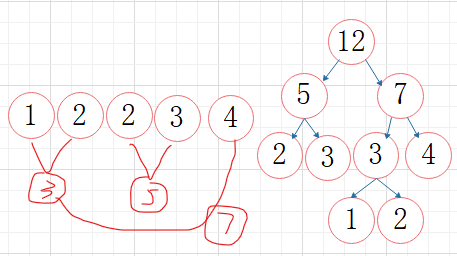
应用:哈夫曼编码
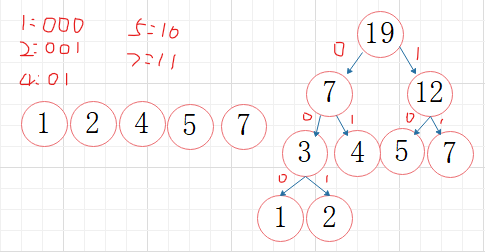
左数为0,右树为1
6、并查集
(查找某个元素所属的集合、合并2个元素各自专属的集合等)
应用:朋友圈
初始化!!!
for (i = 1; i <= stuNum; i++)
{
fd[i].data = i; //集合元素
fd[i].rank = 0;
fd[i].parent = i; //双亲初始化指向自已
}
查找所在集合编号(根节点编号)
int FIND_SET(UFSTree& fd, int x)
{
if (x != fd[x].parent)//双亲不是自已
return(FIND_SET(fd, fd[x].parent));//递归在双亲中找x
else
return(x);//双亲是自已,返回x(找到根节点)
}
集合合并
x = FIND_SET(fd,x); //查找x所在朋友圈的编号
y = FIND_SET(fd,y); //查找y所在朋友圈的编号
if (x == y)
{
return;
}
if (fd[x].rank > fd[y].rank) //y结点的秩小于x结点的秩
{
fd[y].parent = x; //x作为y的双亲结点
fd[x].num = fd[y].num + fd[x].num; //两朋友圈人数相加
}
else
{
fd[x].parent = y; //y作为x的双亲结点
if (fd[x].rank == fd[y].rank)
fd[y].rank++; //y结点的秩增1
fd[y].num = fd[y].num + fd[x].num; //两朋友圈人数相加
}
1.2.谈谈你对树的认识及学习体会
1、关于串:kmp算法还是有点绕,移动规律和数组有点对不上
2、关于树:大致对于建树遍历树和树的应用(哈夫曼树等等)都基本了解,但是中序和前序、后序建树的字符查找还没有很熟练掌握
注意点:
①是顺序存储结构建树(左孩子lchild:2i,右孩子rchild:2i+1),还是采用先序建树(i++)
②递归时,正确设置返回条件,避免返回到一半中断或溢出
(经常和栈,队列结合使用,例如层次遍历)
2.阅读代码
2.1 题目及解题代码
二叉树的锯齿形层次遍历
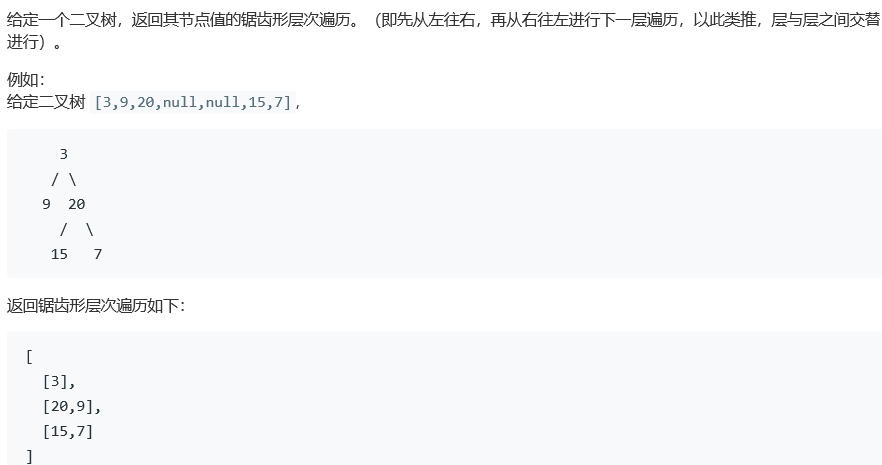
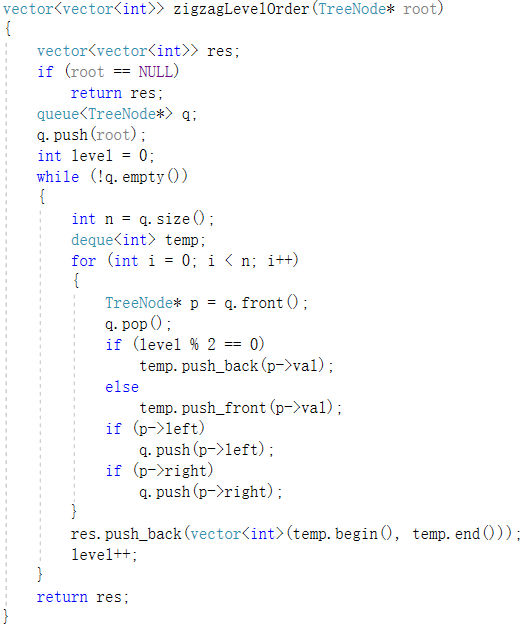
2.1.1 该题的设计思路
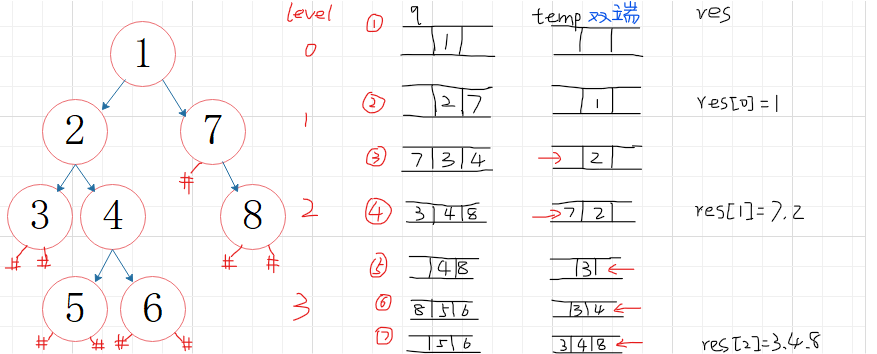
利用双端队列deque
先进先出,则将新元素添加到队列尾部,后插入的元素就可以排在后面;(偶数层)
先进后出,则将新元素添加到队列首部,后插入的元素就可以排在前面;(奇数层)
2.1.2 该题的伪代码
vector<vector<int>> res定义res
定义队列q辅助层次遍历树
从level=0开始
while(层次遍历队列不为空)
deque<int> temp定义双端队列存储每层的节点值
for i = 0 to 当前队列元素个数 do
出队对头元素q.front()
若为偶数层,输出顺序从左往右(从后添加push_back)
若为奇数层,输出顺序从右往左(从前添加push_front)
若对头元素有左右孩子,入队列q
end for
将双端队列中的元素顺序添加到res中
res.push_back(vector<int>(temp.begin(), temp.end()))
2.1.3 运行结果

2.1.4分析该题目解题优势及难点。
1、利用双端队列:队列的两端分别称为前端和后端,两端都可以入队和出队(仍是线性结构)
2、时间复杂度较小,利用双端队列运行速度较快
3、c++vector的用法不是很了解,为了这个题目还特地去看了stl的vector用法(定义,存储方式和输出方式)
vector<vector<int>> res(相当于动态二维数组)
for (i = 0; i < res.size(); i++)
{
cout << "[ ";
for (j = 0; j < res[i].size(); j++)
{
cout << res[i][j]<<"," ;
}
cout <<" ]" <<endl;
}
2.2 题目及解题代码
二叉树剪枝

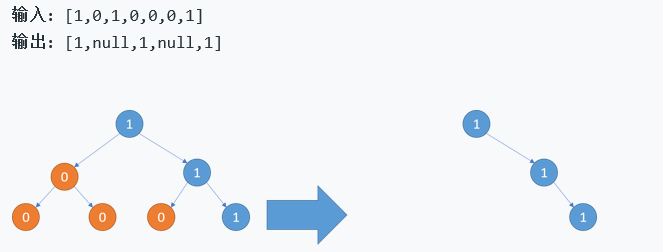

2.2.1 该题的设计思路
先遍历左数,再右树,最后再根,所以后序遍历才能完全剪枝
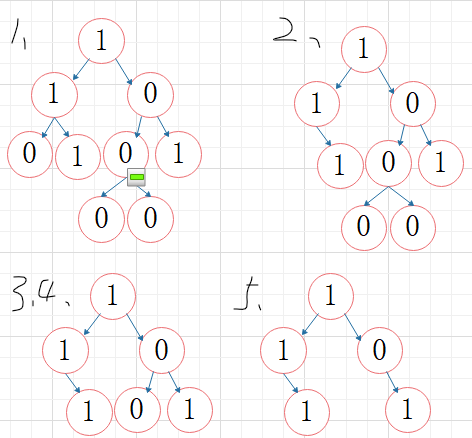
2.2.2 该题的伪代码
后序遍历递归
if (!root) return root;
后序遍历树
root->left = pruneTree(root->left);
root->right = pruneTree(root->right);
若该结点为叶子结点且val为0,剪枝(释放结点且return NULL)
return root;
2.2.3 运行结果
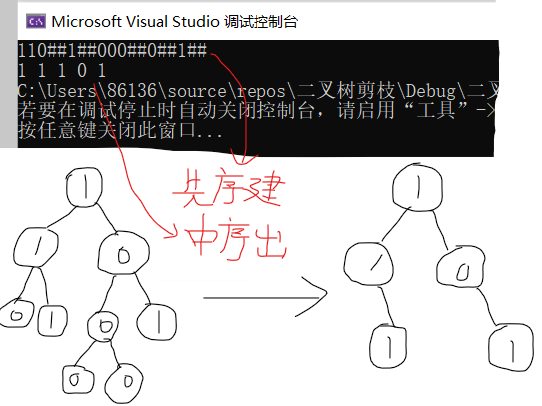
2.2.4分析该题目解题优势及难点。
1、递归算法,代码更简洁,可读性强
2、要考虑是哪种顺序的遍历,例如先序遍历就可能会导致不完全剪枝
3、注意:并不是只要剪掉所有值为0的叶子结点,叶子结点剪完之后,非叶子结点也可能变成叶子结点
4、递归算法其实算是一个难点,有时候跟着跟着就会乱掉,画图还是比较有用的,借图会更好理解
2.3 题目及解题代码
二叉搜索树中的搜索
方法一(迭代)

方法二(递归)
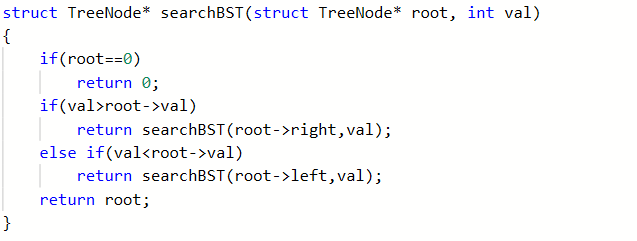
2.3.1 该题的设计思路
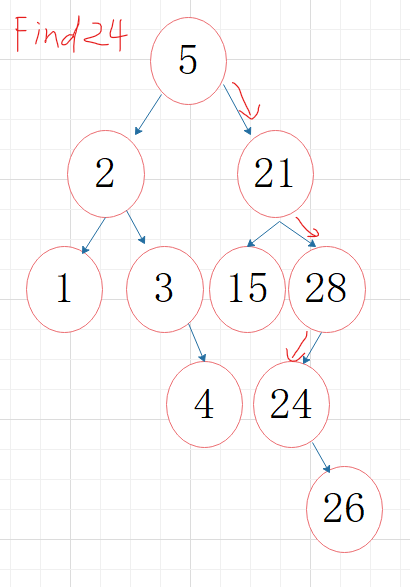
2.3.2 该题的伪代码
二叉搜索树每个节点都有的特点:
大于左子树上任意一个节点的值;
小于右子树上任意一个节点的值;
迭代法
struct TreeNode* searchBST(struct TreeNode* root, int val)
{
while(根节点不空 root != null )
如果根节点是目的节点
return root
如果 val < root.val
查找根节点的左子树 root = root.left
如果 val > root.val
查找根节点的右子树 root = root.right
return 0;
}
递归
struct TreeNode* searchBST(struct TreeNode* root, int val)
{
如果根节点为空或根节点是目的结点 val == root.val
返回root
如果 val < root.val,进入根节点的左子树查找
searchBST(root.left, val)
如果 val > root.val,进入根节点的右子树查找
searchBST(root.right, val)
返回root
}
2.3.3 运行结果
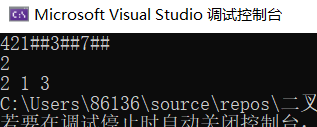
2.3.4分析该题目解题优势及难点。
1、利用迭代法降低了空间复杂度
2、可读性较强
3、遍历特殊二叉树不一定要用递归法,递归所占空间较大,但是胜在代码比较简洁
2.4 题目及解题代码
二叉树最大宽度
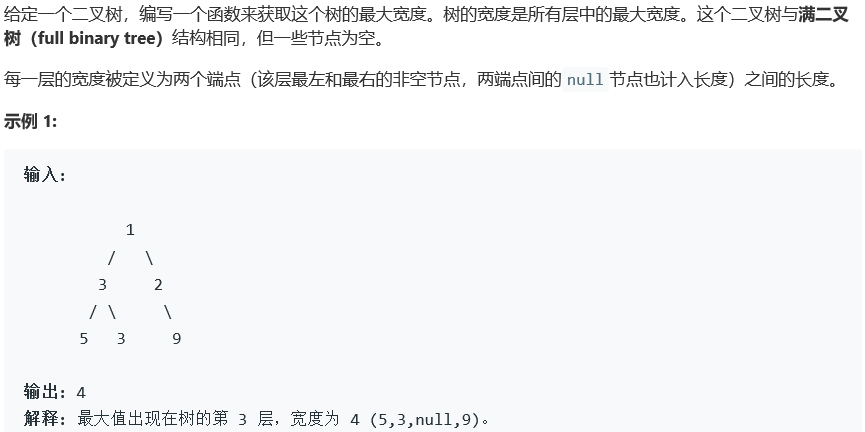

2.4.1 该题的设计思路
每个节点一个 position 值
如果向左子树,那么 position -> position * 2
如果向右子树,那么 position -> positon * 2 + 1
遍历每个节点时,记录节点的 position 信息
第一个遇到的节点是最左边的节点,最后一个到达的节点是最右边的节点。
2.4.2 该题的伪代码
int widthOfBinaryTree(TreeNode* root)
{
定义队列存结点及结点位置
queue<pair<TreeNode*, unsigned long long>> q;
入队根结点q.push({root, 1});
while 队列不为空
求出最大宽度ans = max(int(q.back().second - q.front().second + 1), ans);
队列中保存每个节点的指针以及pos值
若有左右孩子,入队
if (node->left) q.push({node->left , 2 * pos});
if (node->right) q.push({node->right, 2 * pos + 1});
每层的宽度为队尾pos-队首pos+1
return ans;
}
2.4.3 运行结果

2.1.4分析该题目解题优势及难点。
1、利用队列存储两个变量:结点和结点位置,记录位置后更方便计算每层宽度(队尾pos-队首pos+1)
2、max函数方便比较大小
3、解题思路很新颖,这种队列的存储方法也是看了这题后才知道